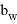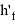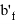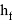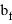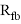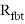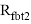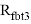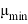Ключевые слова: несущая способность, диаграммный метод, двутавровое сечение, ЦЗО.
Активное развитие сферы производства строительных материалов, включая композитные материалы, приводит к созданию инновационных и уникальных продуктов с высокими показателями надежности, долговечности и низкой стоимостью. Особое внимание уделяется конструкциям с различными видами армирования, такими как дисперсное и комбинированное армирование.
Рассматривая расчет прочности по нормальным сечениям изгибаемых элементов по [1], можно отметить, что не предоставлен расчет на изгиб двутаврового сечения. Продолжая методику расчёта, так же рассмотрим такую переменную как циклы замораживания-оттаивания (далее ЦЗО) и их влияние на конструкцию. Работы [2, 3] провели исследование сталефибробетонных конструкций, используя нелинейную деформационную модель. В работах [4, 5] был рассмотрен расчет изгибаемых элементов сталефибробетонных конструкций по предельным усилиям.
Нормы проектирования сталефибробетонных конструкций СП 360.1325800.2017 «Конструкции сталефибробетонные. Правила проектирования», введенные в действие с 2018 года, вместе с работой о методах расчета и правилах конструирования [6], предполагают возможность расширения их применения в практике проектирования.
Расчетные сопротивления бетона в зависимости от его класса принимают по СП 52–101–2003. Расчетные значения сопротивления бетона сжатию умножаются на коэффициент условия работы. При воздействии низкой температуры значение коэффициента принимают по СП 52–105–2009.
Таким образом, влияние стальных фибр на прочностные и деформационные характеристики сталефибробетона учитывается только при растяжении и не учитывается при сжатии. А работа конструкции после ЦЗО регламентируется коэффициентом условия работы.
Рассмотрим расчет изгибаемых элементов сталефибробетонных конструкций двутаврового сечения в двух вариантах рисунок 1.
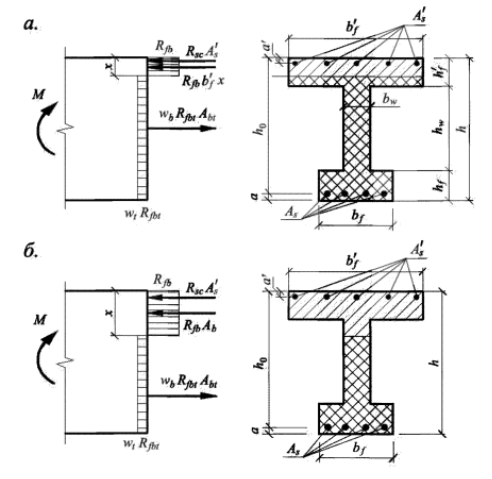
Рис. 1. Положение границы сжатой зоны в сечении изгибаемого сталефибробетонного элемента с арматурой: а — в полке; б — в ребре
Методика расчета требуемой площади поперечного сечения продольной растянутой арматуры в изгибаемом сталефибробетонном элементе двутаврового профиля с одиночным армированием с границей, проходящей в полке.
Исходные данные: h — высота сечения элемента; h
f
– высота сечения растянутой полки; b
f
—
ширина сечения растянутой полки; h’
f
– высота сечения сжатой полки; b’
f
—
ширина сечения сжатой полки; bw
—
ширина сечения ребра;
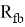
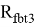
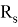
Задаемся значением параметра (расстояние от центра тяжести растянутой арматуры до растянутой грани элемента) и определяем значение рабочей высоты сечения:
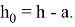
Определяем высоту сечения ребра:
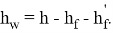
Проверяем условие:
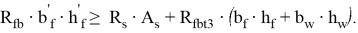
Если условие (1) выполняется, то
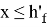
Уравнение равновесия продольных усилий:
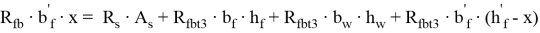
Приравняем несущую способность по нормальному сечению к изгибающему моменту от нагрузки:
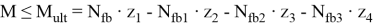
где:
– усилия в сжатой части полки
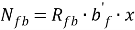
– усилия в растянутой части полки
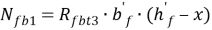
– усилия в ребре
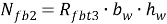
– усилия в растянутой полке
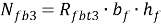
– расстояние от центра тяжести сжатой зоны полки сталефибробетона до центра тяжести продольной растянутой арматуры
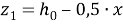
– расстояние от центра тяжести растянутой зоны полки сталефибробетона до центра тяжести продольной растянутой арматуры
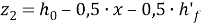
– расстояние от центра тяжести растянутого ребра сталефибробетона до центра тяжести продольной растянутой арматуры
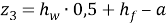
– — расстояние от центра тяжести растянутой полки сталефибробетона до центра тяжести продольной растянутой арматуры
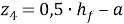
Приравняем несущую способность к моменту от внешних воздействий:
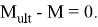
Тогда:
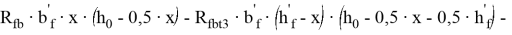
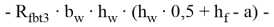
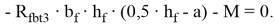
Уравнение (3) представим в виде:
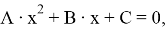
где:
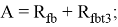
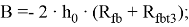
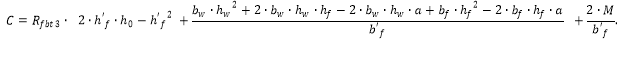
Расчетную высоту сжатой зоны бетона найдем из решения квадратного уравнения (4) в виде:
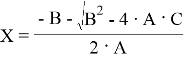
Проверяем условие:
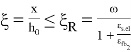
Если условие (5) выполняется, то требуемая площадь сечения продольной растянутой арматуры:
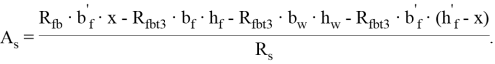
Далее по сортаменту подбираем продольную арматуру и выполняем конструирование.
Если условие (5) не выполняется, то можно установить рабочую арматуру в сжатую зону.
Методика расчета требуемой площади поперечного сечения продольной растянутой арматуры в изгибаемом сталефибробетонном элементе двутаврового профиля с одиночным армированием с границей, проходящей в ребре.
Исходные данные: h — высота сечения элемента; h
f
– высота сечения растянутой полки; b
f
—
ширина сечения растянутой полки; h’
f
– высота сечения сжатой полки; b’
f
—
ширина сечения сжатой полки; bw
—
ширина сечения ребра;
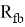
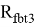
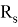
Задаемся значением параметра (расстояние от центра тяжести растянутой арматуры до растянутой грани элемента) и определяем значение рабочей высоты сечения:
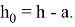
Определяем высоту сечения ребра:
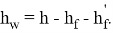
Проверяем условие (1). Если условие не выполняется, то
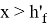
В таком случае уравнение равновесия продольных усилий:
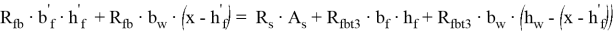
Приравняем несущую способность по нормальному сечению к изгибающему моменту от нагрузки:
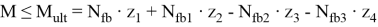
где:
– усилия в сжатой полке
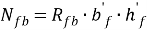
– усилия в сжатой части ребра
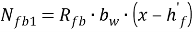
– усилия в растянутой части ребра
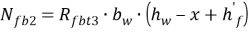
– усилия в растянутой полке
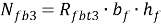
– расстояние от центра тяжести сжатой полки сталефибробетона до центра тяжести продольной растянутой арматуры
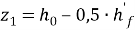
– расстояние от центра тяжести сжатой зоны ребра сталефибробетона до центра тяжести продольной растянутой арматуры
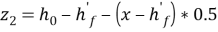
– расстояние от центра тяжести зоны растянутого ребра сталефибробетона до центра тяжести продольной растянутой арматуры
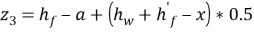
– расстояние от центра тяжести растянутой полки сталефибробетона до центра тяжести продольной растянутой арматуры
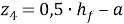
Приравняем несущую способность к моменту от внешних воздействий:
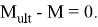
Тогда:
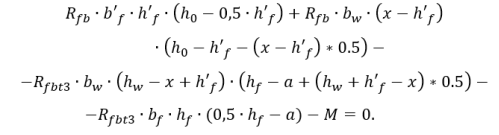
Уравнение (7) представим в виде:
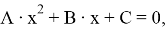
где:
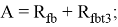
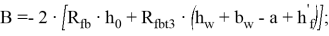
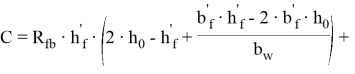
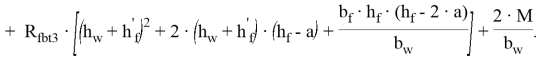
Расчетную высоту сжатой зоны бетона найдем из решения квадратного уравнения (4) в виде:
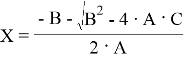
Проверяем условие:
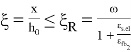
Если условие (9) выполняется, то требуемая площадь сечения продольной растянутой арматуры:
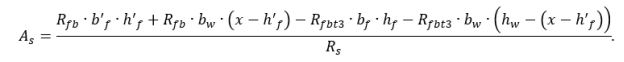
Далее по сортаменту подбираем продольную арматуру и выполняем конструирование.
Если условие (9) не выполняется, то можно установить рабочую арматуру в сжатую зону.
Сравнение результатов расчета по методу предельных усилий и по диаграммному методу, а также разница между несущей способностью до и после воздействия десяти ЦЗО представлены в таблице 1. На рисунках 2 и 3 показаны результаты расчетов диаграммным методом.
Таблица 1
|
Параметры |
ЦЗО — 0 циклов |
ЦЗО — 10 циклов |
|
Исходные данные | ||
|
h, мм |
400 |
400 |
|
|
50 |
50 |
|
|
75 |
75 |
|
|
150 |
150 |
|
|
75 |
75 |
|
|
150 |
150 |
|
|
17 |
11,9 |
|
|
3,7 |
3,33 |
|
|
1,54 |
1,386 |
|
|
0,77 |
0,693 |
|
M , кН . м |
50 |
50 |
|
Метод предельных усилий | ||
|
|
1,20 |
1,28 |
|
Δ , % |
6,3 | |
|
Диаграммный метод | ||
|
|
1,003 |
1,14 |
|
Δ , % |
12,1 | |
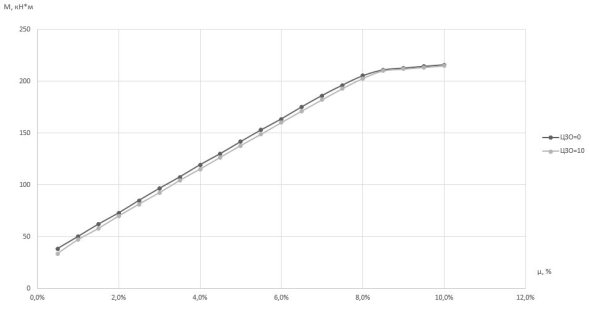
Рис. 2. Зависимость несущей способности от процента армирования
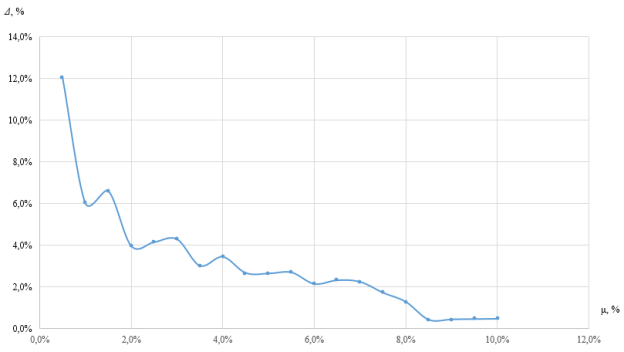
Рис. 3. Разница в % между несущей способностью до и после воздействия ЦЗО.
Литература:
- Попов В. М., Кондратюк В. В. Особенности расчета изгибаемых элементов сталефибробетонных конструкций по нормальным сечениям // Жилищное строительство. 2022. № 4. С. 46–54.
- Морозов В. И., Опбул Э. К. Расчет изгибаемых сталефиброжелезобетонных элементов по нелинейной деформационной модели с использованием опытных диаграмм деформирования сталефибробетона // Вестник гражданских инженеров. 2016. № 5 (58). С. 51–55.
- Опбул Э. К., Дмитриев Д. А., Ведерникова А. А. Нелинейно-итерационный расчет прочности сталефиброжелезобетонных элементов с использованием опытных диаграмм деформирования материалов // Вестник гражданских инженеров. 2017. № 1 (60). С. 79–91.
- Мухамедиев Т. А. Расчет по прочности изгибаемых фибробетонных конструкций методом предельных усилий // Строительная механика и расчет сооружений. 2016. № 5. С. 12–18.
- Попов В. М., Суворов И. В. Некоторые особенности расчета изгибаемых элементов из сталефибробетона при комбинированном армировании // Вестник гражданских инженеров. 2014. № 3 (44). С. 88–91.
- ОПБУЛ Э. К. Эффективное использования высокопрочной арматуры в изгибаемых элементах без предварительного напряжения: специальность 05.23.01 «Строительные конструкции, здания и сооружения»: диссертация на соискание ученой степени кандидата технических наук / ОПБУЛ Эрес Кечил-оолович; Санкт-Петербургский государственный архитектурно-строительный университет. — Санкт-Петербург, 2005. — 151 c.