Упрощение математической модели



Сформулированная краевая задача в работе [1, с. 3] достаточно сложная и требует для своего решения значительных усилий. Поэтому мы укажем здесь возможные пути её упрощения.

Прежде всего заметим, что в рамках настоящей работы мы будем рассматривать только стационарные колебания рассматриваемого тела с несущей круговой частотой , равной круговой частоте воздействия. Примем, что в граничном условии (13) в [1], f(t) 1, =0.

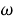
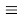
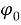
Будем искать решение задачи в виде , где - вещественная векторная функция. Тогда, очевидно, и граничные условия (13) на участке с сводятся к следующим

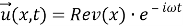
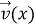
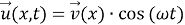
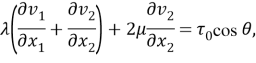
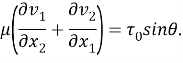
Уравнения (5) в [1] переходят в систему уравнений эллиптического типа

( A+ , (x );

(x ;

(x .

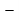
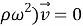
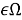
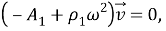
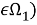
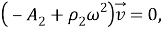
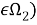
Все однородные граничные условия и условия сопряжения сохраняют свой вид, но вместо , в них теперь должны фигурировать , Начальные условия (14) в [1] для рассматриваемой задачи теряют смысл.

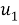
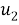
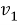
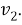
Второй способ упрощения задачи связан с тем фактом, что толщина дефекта в типичных случаях значительно меньше его длины, т.е , .

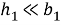
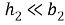
Это дает возможность отказаться от изучения подробностей волнового поля внутри дефектов и не рассматривать уравнений движения в областях и . В такой интерпретации дефекты трактуются как линии:

.

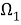
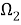
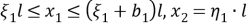
Аналогично , .

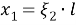
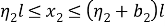
Рассмотрим горизонтальный дефект, представляющий собой прямоугольник длиной и толщиной h. Временно расположим ,

так, как указано на рис.1.

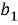
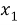
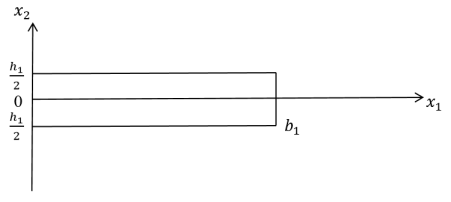
Рис. 1

Мы предположим, что . В силу этого можно ограничиться линейной аппроксимацией зависимости от компонент вектора перемещений , (напомним, что рассматривается плоская деформация).

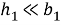
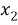
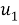
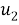
Таким образом, можно написать

, (1)

.

Здесь -новая неизвестная функция, связанная, как легко убедиться, с углом поворота нормали к оси дефекта и деформации. Коэффициент при в выражении для равен в силу равенства . Зависимость рассмотриваемых величин от t мы временно не указываем. Из (1) следует аппроксимация для деформаций

,

,

,

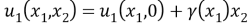
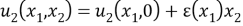
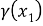
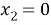
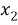
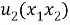
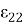
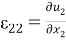
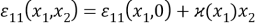
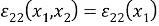
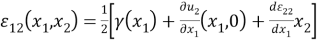
здесь .

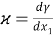
Введем в рассмотрение перемещения берегов дефекта :

,

.

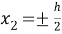
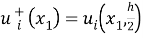
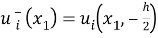
Используя (1), можно получить

, ,

, .

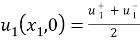
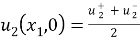
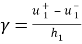
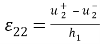
Таким образом, мы получаем аппроксимацию перемещений в виде

,

.

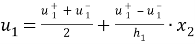
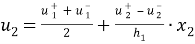
Отсюда следует аппроксимация деформаций

,

,

.

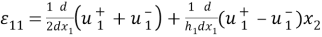
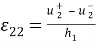
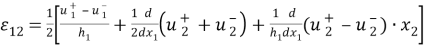
В упрощенной подстановке, когда горизонтальное включение трактуется как линия, сформулированная в [1] задача состоит в нахождении вектора u ( x , t ), удовлетворяющего уравнениям (4) в [1], в области

, представляет собой прямоугольник с выброшенной линией, которую занимает включение.

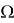
Литература:

1. Международный научный журнал «Молодой ученый» N44 (491), ноябрь 2023г., URL:https://moluch.ru/archive/491/107261/.
2. Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. -М.: Наука, 1986.
3. Harimi К. Scattering of aplane wales by a cavitg Ribbon in a Solid //Journal of Applied Phisics. -1962.-v.33, N12