В данной статье исследуется важность приведения системы сил к центру и ее влияние на статику и динамику механических систем.
Ключевые слова: жесткая заделка, сила, активная сила, силовой треугольник, плоская система сил, линия действия равнодействующей.
Приведение системы сил к данному центру — важная составляющая любой задачи статики и динамики [1]. Эта операция необходима при моделировании нагрузки механических систем и выбора метода решения задачи.
Иногда возникают ситуации, когда система сил может быть рассмотрена как более простая по числу степеней свободы. Так, зачастую, теорема о трёх силах переводит произвольную плоскую систему сил в систему сходящихся сил.
Рассмотрим случай приведения системы сил к данному центру при наличии в конструкции жёсткой заделки (рис. 1). В общем такая система относится к типу произвольной (в нашем случае плоской) системе, и приводится к данному центру в виде главного вектора сил и главного момента.
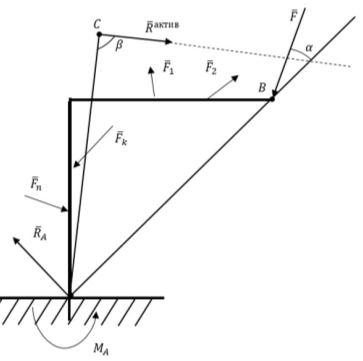
Рис. 1. Расчётная схема действия плоской системы сил при наличии жёсткой заделки
Но могут быть случаи приведения системы к равнодействующей, то есть к системе сходящихся сил [2]. Проанализируем все возможные детали этой задачи.
- Всякая система активных сил может быть приведена к равнодействующей в точке плоскости (пространства), координата которой определяется по соответственной методике.
-
Если среди активных сил есть одна сила, неизвестная по величине, то систему можно рассматривать в виде трёх действующих сил: силы реакции в заделке
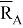
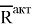
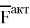
При соблюдении условия, что линия действия равнодействующей активных сил
, и неизвестной по величине активной силы
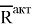
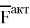
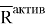
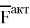
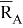
Рис. 2. Расчётная схема действия плоской системы сил при наличии жёсткой заделки в случае образования системы сходящихся сил
Действующие силы при этом образуют силовой треугольник. На рисунке 3 показан силовой треугольник, из решения которого определится величина и направление реакции жесткой заделки
.(1)
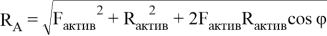
Величина силы
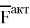
Момент жесткой заделки будет в этом случае равен нулю.
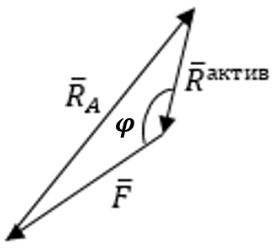
Рис. 3. Силовой треугольник системы сходящихся сил при наличии жёсткой заделки
В противном случае полученная система трёх сил не будет сходящейся, так как, по теореме о трёх силах она должна быть уравновешенной, так как реакция жёсткой заделки хотя будет противоположна равнодействующей всех активных сил, но её линия действия не проходит через точку [1] приложения равнодействующей плоской системы активных сил (рис. 4).
При этом реакция жёсткой заделки будет состоять из реактивной силы
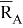
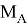
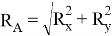
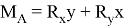
где
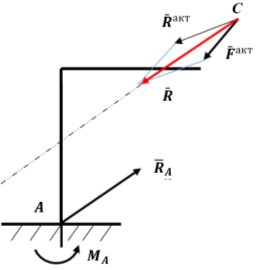
Рис. 4. Расчётная схема действия равнодействующей активных сил
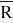
Таким образом, в случае если линия действия равнодействующей активных сил
не пересекает точку крепления жёсткой заделки, то действие теоремы о трёх силах не будет распространяться для данной системы трёх сил, а равновесие системы будет наступать при добавлении момента пары сил жёсткой заделки.
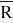
Полученная в последнем случае система сил также не будет образовывать силовой треугольник.
Выводы:
— в уравновешенной плоской системе сил, при наличии жёсткой заделки, силовой многоугольник (треугольник) не будет замкнутым, без приведения данной системы сил к центру;
— исключение составляет случай, когда линия действия равнодействующей активных сил будет пересекать точку крепления жёсткой заделки.
Литература:
- Яблонский А. А., Никифорова В. М. Курс теоретической механики: Учебник. 11-е изд., стер. СПб.: Издательство «Лань», 2004–768 с.: ил.— (Учебники для вузов. Специальная литература).
- Мещерский И. В. М 56 «Задачи по теоретической механике» Учебное пособие 49-е изд. Стер./ Под редакцией В. А. Пальмова, Д. Р. Меркина. СПб.:Издательство «Лань»,2008–448 с.:ил.— (Учебники для вузов. Специальная литература).
