Сатниязова, Э. К. Приведение дифференциальных уравнений в частных производных с постоянными коэффициентами к каноническому виду / Э. К. Сатниязова, Оразгали Бахтыбай улы Боранбаев, Д. К. Убайдуллаева, Рахим Осербай улы Онгарбаев. — Текст : непосредственный // Молодой ученый. — 2023. — № 27 (474). — С. 8-12. — URL: https://moluch.ru/archive/474/104824/ (дата обращения: 02.05.2024).
Вопрос о классификации частных дифференциальных уравнений второго порядка с двумя переменными и их канонической формы имеет большое значение при работе с уравнениями математической физики. Этот вопрос имеет большое значение в технике и в жизни в связи с задачами, решаемыми данным уравнением. Часто мы приводим уравнение к каноническому виду, подставляя функции одной или двух переменных. Однако в общем случае этот тип канонического представления может усложниться. Следовательно, мы должны упростить его снова. Вот несколько примеров того, что делать в такой ситуации:
Задача 1.
Привести следующие уравнения с постоянными коэффициентами к каноническому виду, затем еще раз упростить.
.(1)
,
,
.
— уравнение гиперболического типа.
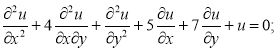
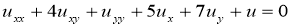
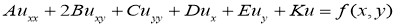
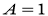
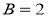
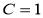
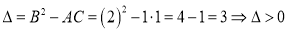
Приведем данное уравнение к каноническому виду:
Характеристическое уравнение данного уравнения:
;
;
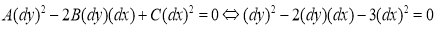
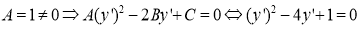
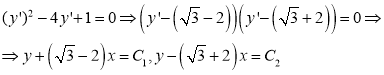
Теперь, если мы возьмем
и отметим
, то
;
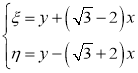
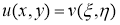
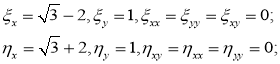
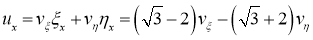
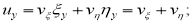
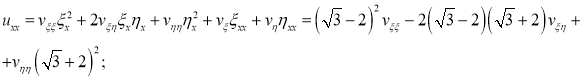
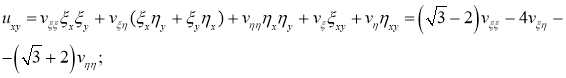
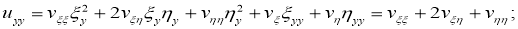
Ставим найденные значения на соответствующие места в уравнении (1):
- мы привели его в канонический вид, теперь нам нужно еще больше упростить каноническую форму условием.
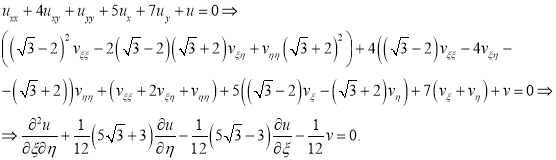
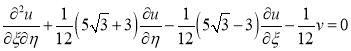
Для дальнейшего упрощения канонической формы сделаем следующую замену:
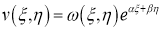
Затем
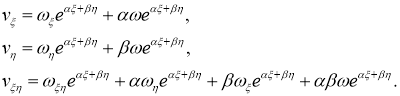
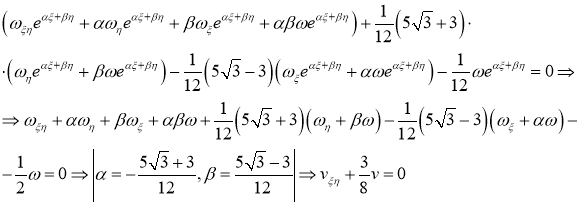
Ответ:
, здесь
,
.
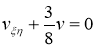
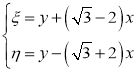
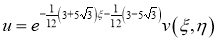
Задача 2
. Привести следующие уравнения с постоянными коэффициентами к каноническому виду, затем еще раз упростить.
.(1)
,
,
.
— уравнение эллиптического типа.
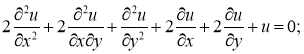
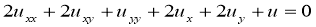
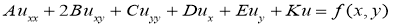
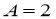
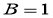
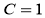
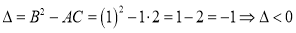
Приведем данное уравнение к каноническому виду:
Характеристическое уравнение данного уравнения:
;
;
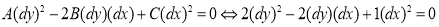
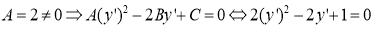
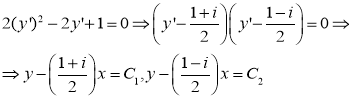
Теперь, если мы возьмем
и отметим
, то
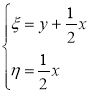
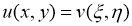
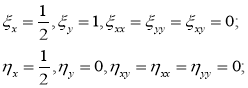
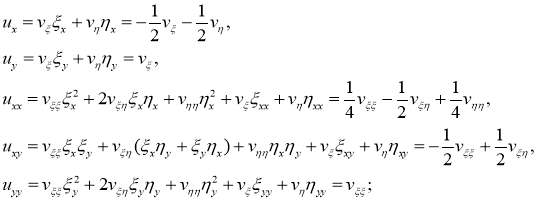
Ставим найденные значения на соответствующие места в уравнении (1):
— мы привели его в канонический вид, теперь нам нужно еще больше упростить каноническую форму условием.
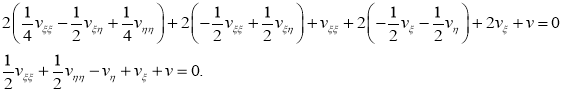
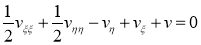
Для дальнейшего упрощения канонической формы сделаем следующую замену:
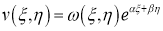
Затем
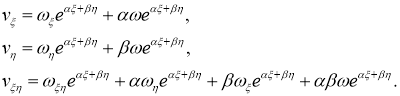
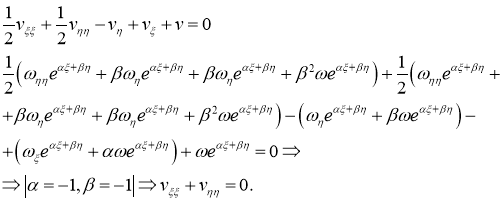
Ответ:
, здесь
,
.
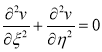
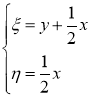
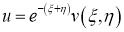
Литература:
Омаров А., Курбанбаев О. О., Кылышбаева Г. К., Методы решения задач математической физики, Учебное пособие для студентов вузов — 2017. -228c
Агошков В. И., Методы решения задач математической физики: Учебное пособие для студентов вузов, — М.:Физматлит, 2002. –320 с.
Бицадзе А. В.. Уравнения математической физики. — М.: Наука, 1982–336 с.
Программа предназначена для освоения студентами разностного метода решения уравненийгиперболическоготипа и может применяться в учебном процессе. В данной работе рассматривается проблема построения явной разностной схемы.
Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы. Об одной краевой задаче для нагруженного уравнения параболо-гиперболическоготипа, вырождающегося внутри области.
Для функции (9) применяем (4), находим . Тогда решение поставленной задачи имеет следующий вид: Двойную спираль ДНК, циклы солнечной активности и сложные электронные сигналы математически можно представить в виде ряда волнообразных кривых.
Несколько нам известно, краевые задачи типа задачи Трикоми и Геллерстедта для вырождающегося нагруженного уравнения смешанного типа второго порядка исследовались сравнительно мало.
Программа предназначена для освоения студентами разностного метода решения уравненийгиперболическоготипа и может применяться в учебном процессе. В данной работе рассматривается проблема построения явной разностной схемы.
Эквивалентность характеристической задачи для уравнения смешанного типа задачи Коши для симметрической гиперболической системы. Об одной краевой задаче для нагруженного уравнения параболо-гиперболическоготипа, вырождающегося внутри области.
Для функции (9) применяем (4), находим . Тогда решение поставленной задачи имеет следующий вид: Двойную спираль ДНК, циклы солнечной активности и сложные электронные сигналы математически можно представить в виде ряда волнообразных кривых.
Несколько нам известно, краевые задачи типа задачи Трикоми и Геллерстедта для вырождающегося нагруженного уравнения смешанного типа второго порядка исследовались сравнительно мало.
