Топологическая эквивалентность путевого развития железнодорожных станций



В статье авторы рассматривают вопросы, связанные с эквивалентностью путевого развития железнодорожных станций. Путевое развитие представляется в виде графов, включая деревья горловин различных парков. Показана связь бинарных деревьев с числами Каталана, а также — эффективность использования топологических индексов Рандича и Виттена в решении задач эквивалентности.

Ключевые слова: железнодорожные станции, горловины, графы, деревья, топологический индекс, эквивалентность.

1. Предварительные сведения. Для начала приведем некоторую известную терминологию, относящуюся к эксплуатации железных дорог и теории графов.

Железнодорожной станцией называется раздельный пункт железных дорог, с наличием путевого хозяйства и обеспечивающем работы по приёму, отправке, скрещению и обгону, регулированию движения поездов, по приёму, выдаче грузов, багажа и грузобагажа, возможность обслуживать пассажиров [2]. При достаточной оборудованности путевыми устройствами железнодорожной станции, также проводятся технические операции с поездами, маневровые работы, расформирование и формирование поездов.

С 2004 года в науке о проектировании железнодорожных станций и узлов используется методология классической теории графов, преимущественно для выполнения комбинаторных расчетов числа вариантов горловин различных парков станций. Например, в работе [2] приводится способ вычисления необходимого числа стрелочных переводов в горловине сортировочного парка, основанный на классической теореме Л. Эйлера о многогранниках, позволяющей определить зависимость между количеством путей в сортировочном парке, количеством путей роспуска и количеством стрелочных переводов, соединяющих всю конструкцию в путевое развитие горочного сортировочного устройства. В работе [1] метод В. Г. Шубко рассмотрен с точки зрения топологии двумерных поверхностей, что позволяет вложить в них графы горочных горловин для дальнейшего анализа.

Граф путевого развития железнодорожной станции — это математический объект, используемый в теории графов для моделирования отношений между объектами. Граф представляет собой совокупность точек (вершин) и линий (ребер), которые соединяют вершины.

Формально, такой граф определяется как пара множеств , где — множество вершин (стрелочных переводов станции), а — множество ребер (путевое развитие станции), которые соединяют вершины. Ребро соединяет вершины

и .

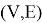
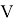
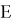
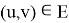
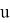
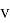
2. Способ задания путевого развития станции. Одним из способов задания путевого развития железнодорожной станции является составление матрицы смежности.

Матрица смежности — это матрица, которая используется в теории графов для представления связей (смежности) между вершинами графа. Матрица смежности является квадратной матрицей размера , где — количество вершин в графе.

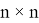
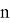
Пусть дан граф , где — множество стрелочных переводов в графе, а — множество ребер (путевого развития) графа. Матрица смежности графа определяется следующим образом:

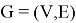
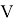
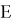
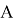
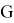
Для железнодорожных станций ребра в графе — неориентированны, а значит матрица смежности является симметричной относительно главной диагонали.

Матрица смежности содержит информацию о связях между стрелочными переводами графа. Например, длину ребра (участка железнодорожного пути) можно указать в матрице смежности в качестве веса ребра.

3. Горловина станции как бинарное дерево. Горловина железнодорожной станции — это связный граф без циклов и с стрелочными переводами, где ребро (путевое развитие). Обозначим как , где — множество вершин, а — множество ребер.

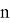
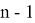
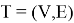
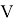
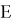
Граф-дерево обладает следующими свойствами:

1. Один связный компонент: горловина станции всегда является связной, то есть между любыми двумя стрелочными переводами найдется путь.
2. Без циклов: горловина не имеет циклов. Это означает, что любые два стрелочных перевода соединены только одним путем.
3. ребро: количество ребер в горловине станции всегда на единицу меньше количества стрелочных переводов. Формально: .
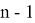
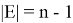
4. Единственный путь между стрелочными переводами: между любыми двумя стрелочными переводами существует единственный путь.
5. Горловина станции является минимальным связным графом: она имеет минимальное число ребер среди всех связных графов с стрелочными переводами.
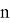
6. Горловина станции — двудольный граф: граф-дерево является двудольным графом, то есть его вершины можно разбить на две доли так, чтобы все ребра шли между ними.

Для любого стрелочного перевода в горловине станции степень равняется 3.

Степень стрелочного перевода — это количество ребер, инцидентных данному стрелочному переводу. Формально, для графа и стрелочного перевода , его степень , обозначается как , определяется следующим образом:

,

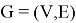
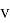
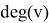
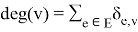
где — дельта-функция Кронекера, которая равна 1, если ребро инцидентно стрелочному переводу , и 0 в противном случае.

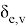
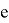
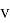
Кроме того, абсолютно любое путевое развитие горловины железнодорожной станции является бинарным деревом, то есть направленным ациклическим графом, в котором каждый стрелочный перевод имеет не более двух дочерних стрелочных переводов.

Любую горловину можно определить рекурсивно. Пустое дерево является бинарным деревом. Если и являются левым и правым поддеревом соответственно, то дерево, у которого корень имеет и

в качестве детей, также является бинарным деревом.

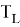
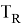
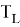
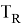
Можно определить горловину станции формально, используя множества и отношение на множестве стрелочных переводов.

Множество стрелочных переводов горловины обозначим , тогда:

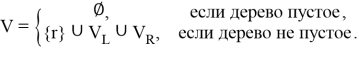
Здесь — корень дерева, а и — множества стрелочных переводов левого и правого поддерева соответственно.

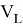
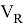
Отношение на множестве стрелочных переводов обозначим

, тогда:

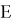
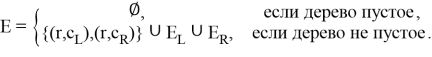
Здесь и — дочерние стрелочные переводы корня , а и — отношения на множествах стрелочных переводов левого и правого поддерева соответственно.

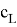
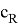
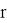
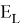
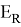
В горловине станции может быть не более одного корня, и каждый стрелочный перевод, кроме корня, имеет одного родителя.

Пример горловины сортировочной горки на 4 пути в виде бинарного дерева представлен на рис. 1:

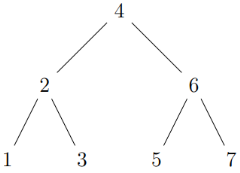
Рис. 1. Граф-дерево горловины сортировочной горки на 4 пути

4. Горочная горловина как алгебраическая полугруппа. Путевое развитие горочной горловины можно также представить в виде алгебраической полугруппы — математического объекта, определяемый парой , где — множество путей в сортировочном парке, а — бинарная операция на этом множестве. Формально, для любых двух путей сортировочного парка , операция определена следующим образом:

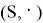
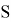
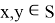
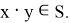
Для того, чтобы множество с операцией было полугруппой, должны быть выполнены две аксиомы:

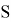
1) Ассоциативность: для любых :

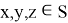
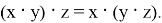
2) Замкнутость: для любых :

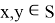
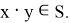
Первая аксиома, ассоциативность, говорит нам, что порядок выполнения операций не имеет значения. Например, если у нас есть три пути в сортировочном парке и , выполнение операции будет одинаково эффективным, если мы выполним операцию или . Это свойство является основой многих математических объектов, таких как моноиды, группы и кольца.

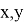
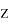
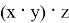
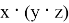
Вторая аксиома, замкнутость, говорит нам, что результат операции всегда будет принадлежать множеству . Это свойство гарантирует нам, что операция будет хорошо определена на множестве , и мы можем безопасно выполнять операции на его элементах.

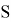
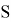
5. Связь с числами Каталана. Числа Каталана — это ряд целых чисел, их формула выглядит следующим образом:

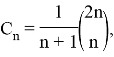
где является натуральным числом.

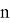
Связь между числами Каталана и ассоциативностью важна для выполнения комбинаторных операций в горловинах железнодорожных станций и заключается в следующем: число сочетаний скобок, при которых выражение с использованием путей, принадлежащих горловине будет ассоциативным, равно

-му числу Каталана. Например, для существует два способа поставить скобки, чтобы выражение было ассоциативным: и . Таким образом, число Каталана равно .

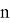
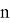
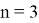
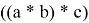
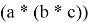
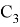
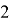
Допустим, у нас есть путей в парке станции: , , ,

, an. Мы должны определить, сколько существует способов поставить скобки так, чтобы результат был ассоциативным. Мы можем начать со скобок вокруг двух первых путей парка: . Теперь нам нужно определить, сколько способов расставить скобки вокруг оставшихся путей парка. Нам нужно выбрать некоторый путь и разбить последовательность на две части: , , , и , , ,

. Затем мы можем рекурсивно вычислить число способов расставить скобки для каждой части и перемножить результаты.

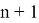
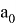
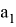
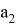
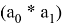
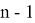
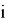
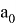
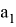
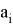
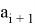
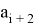
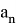
В итоге мы получим выражение:

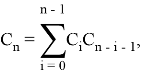
что является рекурсивной формулой, использующейся для вычисления чисел Каталана, а значит и числа вариантов соединения стрелочными переводами путей парка станции в конструкцию самого парка.

Например, для мы можем использовать эту формулу для вычисления следующим образом:

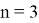
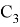
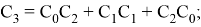
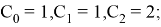
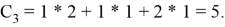
Таким образом, мы получили, что равно , что соответствует тому, что мы ранее увидели.

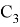
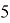
6. Эквивалентность по матрицам смежности. Для определения эквивалентности двух графов по их матрицам смежности, необходимо проверить равенство этих матриц. Два графа считаются эквивалентными, если они имеют одинаковое число вершин и ребер, и при этом каждая вершина одного графа соединена с той же самой вершиной другого графа, идентифицированной по номеру, при условии, что в обоих графах соответствующие ребра имеют одинаковые направления и веса.

Рассмотрим две матрицы смежности и для двух графов и соответственно:

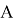
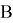
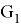
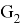
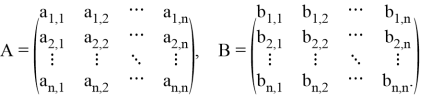
Для того чтобы проверить эквивалентность графов, их матрицы смежности нужно сравнить элемент за элементом и убедиться в том, что они одинаковы. То есть и будут эквивалентными тогда и только тогда, когда для всех будет выполняться равенство .

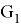
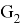
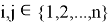
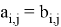
Если матрицы равны, то графы эквивалентны. Если же матрицы отличаются, то графы неэквивалентны.

7. Эквивалентность по топологическому индексу Рандича. Для определения эквивалентности двух графов железнодорожных станций с помощью расчета топологического индекса Рандича необходимо выполнить следующие шаги:

1. Представить каждый граф в виде матрицы смежности размерности , где — количество узлов в графе.
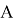
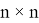
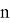
2. Для каждого графа рассчитать сумму элементов матрицы смежности , где .
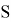
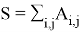
3. Рассчитать топологический индекс Рандича для каждого графа по формуле:

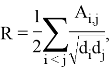
где

и — степени вершин и соответственно.

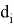
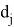
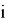
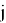
4. Если топологические индексы и для двух графов железнодорожных станций совпадают, то графы эквивалентны.

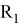
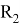
Давайте рассмотрим примеры для двух графов:

Пусть дана для первого графа матрица смежности, имеющая следующий вид:

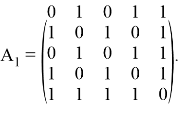
Сумма элементов матрицы смежности для графа 1 равна .

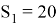
Рассчитаем топологический индекс Рандича для графа 1:

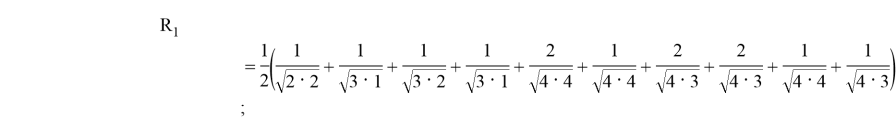
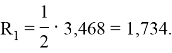
Для графа 2 матрица смежности будет иметь следующий вид:

Сумма элементов матрицы смежности для графа 2 равна .

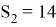
Рассчитаем топологический индекс Рандича для графа 2:

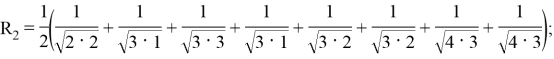
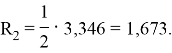
Таким образом, графы 1 и 2 не эквивалентны, так как их топологические индексы Рандича различаются.

8. Эквивалентность по топологическому индексу Виттена. Топологический индекс Виттена — это числовое значение, которое можно вычислить для любого связного графа железнодорожной станции. Он определяется как

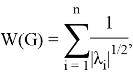
где — число стрелочных переводов на станции, — собственные значения матрицы Лапласа графа станции.

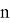
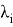
Для того чтобы определить эквивалентность двух графов железнодорожных станций с помощью индекса Виттена, нужно выполнить следующие шаги:

1. Вычислить индекс Виттена для первого графа станции .
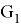
2. Вычислить индекс Виттена для второго графа станции .
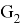
3. Сравнить полученные значения. Если они равны, то графы эквивалентны. Если они отличаются, то графы не эквивалентны.

Доказательство данного метода основывается на следующих фактах:

– если два графа железнодорожных станций эквивалентны, то их матрицы Лапласа будут подобными и, следовательно, будут иметь одинаковый набор собственных значений.

– обратно, если два графа железнодорожных станций имеют различные значения индекса Виттена, то их матрицы Лапласа не могут быть подобными, а значит, графы не могут быть эквивалентными.

Литература:

1. Пазойский, Ю. О. Комбинаторные аспекты горочных горловин технических станций / Ю. О. Пазойский, С. Н. Шмаль, Ж. Янев // Фёдор Петрович Кочнев — выдающийся организатор транспортного образования и науки в России: Труды международной научно-практической конференции, Москва, 22–23 апреля 2021 года / Отв. редактор А. Ф. Бородин, сост. Р. А. Ефимов. — Москва: Российский университет транспорта, 2021. — С. 135–140. — EDN RDFCGJ.
2. Шубко, В. Г. Применение теории графов к конструкции и размещению железнодорожных станций / В. Г. Шубко. — Москва: МИИТ, 2005. — 32 c. — Текст: непосредственный.