Использование квантовых компьютеров при атаке на RSA



Встатье рассмотрены вопросы стойкости криптографического метода RSA в «доквантовую» и «постквантовую» эпохи, приведены примеры использования квантовых компьютеров для ускорения процесса взлома RSA.

Ключевые слова: RSA, алгоритм, атака, защита информации, квантовый компьютер.

В 1977 Ron Rivest, Adi Shamir и Leonard Adleman разработали криптографический метод, названный по первым буквам их фамилий — RSA. В современном мире этот метод является основополагающим во многих системах, например, при защите подключений к сайтам. Так, «Портал государственных услуг» использует криптографический протокол со спецификацией «TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256» [1], где метод RSA используется для шифрованной передачи ключей.

RSA-алгоритм работает следующим образом. У каждого человека есть по два больших, простых числа, которые они никому не раскрывают. Эти числа перемножаются, что дает еще большее число, открытое всем желающим. Отправляя личное сообщение другому человеку, мы шифруем его с помощью большого числа адресата так, чтоб расшифровать его можно было, только зная те два больших множителя, из которых это число получилось. Это алгоритм с ассиметричным ключом — зашифровалось сообщение с помощью одного ключа, а расшифровалось с помощью другого. Для адресата расшифровка не составит особого труда, а вот постороннему человеку придется подбирать числа, из которых получился открытый ключ.

При наличии суперкомпьютера, используя метод решета числового поля, можно подобрать эти числа. Современная криптография использует числа длиной около 232 десятичных знаков. Осуществить подбор чисел, зная лишь их произведение, у суперкомпьютера уйдут сотни триллионов лет, а квантовые компьютеры могут значительно ускорить этот процесс [2].

Почему же квантовый компьютер подбирает простые множители для больших чисел быстрее обычного? Для начала рассмотрим базовые принципы без применения квантовых компьютеров. Возьмем некое число , которое является произведением двух простых чисел и . Возьмем число без общих множителей с числом

. Если возвести g в некоторую степень , то получим [3]:

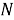
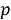
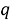
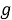
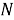
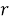
g r = mN + 1,

(1)

где m — коэффициент кратности.

Для примера пусть равно 77, возьмем число меньшее 77, например, равное 8. Перебирая степени g , получаем, что 8 ¹⁰ при делении на 77 дает 1. Применим преобразования к уравнению (1):

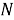
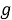
( g r /2 + 1) ( g r /2– 1) = mN + 1

(2)

Известно, что p и q находятся в правой части уравнения. Они же должны лежать и в левой, но умноженные на какой-то коэффициент. Таким образом, мы взяли какое-то случайное значение и, найдя степень r, получили два числа, у которых с большой вероятностью найдутся общие множителя с N :

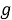
( g r/ 2 + 1) = ( g 10/2 + 1) = 32769 ( g r /2– 1) = ( g 10/2– 1) = 32767

(3)

Чтобы найти общий делитель одного из этих двух чисел и , применим алгоритм Евклида [4].

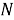
Последовательно производя деление с помощью данного алгоритма, находим что число 11 — делитель как для

, так и . То же самое можно сделать с числом или просто разделить 77 на 11 и получить число . Таким образом, мы нашли и .

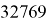
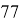
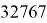
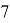
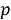
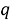
Обобщим, как нам искать простые сомножители p и q .

1. Взять случайное значение g .
2. Выяснить, в какую степень необходимо возвести , чтобы получить .
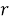
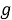
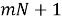
3. Найти два числа с помощью полученной степени, у которых могут быть общие множители с .
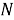
4. Вычислить общие множители этих чисел и с помощью алгоритма Евклида. Таким образом, можно найти и .

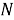
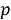
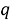
Чтобы произвести все эти действия квантовый компьютер не нужен. Однако квантовые компьютеры ускоряет второй этап этого процесса — поиск степени, в которой нужно возвести , чтобы получить произведение . Рассмотрим, как квантовые вычисления помогают в этом.

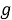
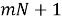
Бит у обычного компьютера может быть всего лишь в двух состояниях — либо 0, либо 1. Если у нас 2 бита, то мы имеем 4 состояния — «00», «01», «10» и «11». Если мы захотим возвести 7 в степень равную какому-то из этих чисел, то придется делать по одному за раз.

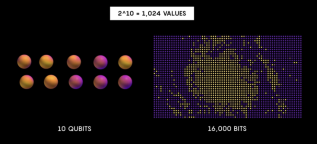
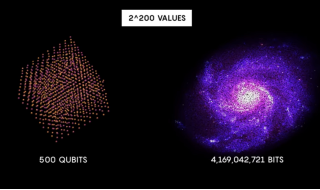
Кубиты в квантовых компьютерах тоже имеют 2 состояния «0» или «1». Но в отличие от обычных битов кубитам необязательно принимать только одно из этих значений. Их состояние — это суперпозиция нуля и единицы. Получается, если у нас 2 кубита, то они могут находиться одновременно в суперпозициях «00», «01», «10» и «11». Если мы проведем возведение числа в какую-нибудь степень, используя квантовый компьютер, то сразу получим суперпозицию всех результатов. Увеличив число кубитов всего до 10, будет возможным одновременно представить больше 16000 состояний. А значит, получим одновременно больше 16000 результатов, что представлено на рисунке 1.

Рис. 1. Производительность квантовых компьютеров (Источник: [5])

Вернемся к . Если мы продолжим возведение в степень больше 10, то заметим, что каждый остаток будет повторяться через 10 степеней, то есть:

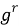
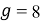
8 10*a mod77 = 1 8 10*a+1 mod77 = 8 ……………….. 8 10*a+9 mod77 = 29,

(4)

где — натуральное число. Таким образом, ясно, что остатки цикличны.

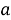
Зная это, можно взять квантовый компьютер и найти множители произведения двух простых чисел. Сначала разделим кубиты на 2 набора. Первым будет набор из суперпозиций 0, 1, 2, 3, 4 … 2 ²⁰⁵⁰ . Для такой суперпозиции понадобится 2050 кубит [6]. Второй набор имеет такой же размер и состоит из нулей. Теперь возводим во все степени состояний из первого набора, делим на и записываем остатки во второй набор. Таким образом, мы запутали 2 набора кубитов.

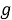
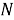
Однако, нельзя просто взять и измерить эту суперпозицию. Так мы получим всего лишь одно случайное значение из возможных, а вся остальная информация теряется. Можно измерить не всю суперпозицию, а только набор с остатками, так мы узнаем значение одного из них, и этот остаток будет встречаться снова и снова, по одному разу в каждом цикле. Так мы получим суперпозицию состояний с одинаковым остатком, а связанные с ними степени будут находиться друг от друга на расстоянии r. Это и есть необходимое нам число. Мы получили периодическую суперпозицию, в которой все элементы разделены расстоянием r . Чтобы извлечь из этой суперпозиции нужное нам число r — частоту (период), с которой в суперпозиции повторяются значения, необходимо применить преобразование Фурье [7], адаптированное под квантовые вычисления в 1994 году Питером Шором и Доном Копперсмитом. Применяя данный алгоритм, мы получаем состояния, равные 1/ r , откуда несложно получить r .

Как видно, математические основы для взлома RSA системы уже готовы. Единственная преграда — отсутствие такого количества кубитов в современных квантовых компьютерах. По оценкам экспертов, в ближайшие 25–30 лет криптосистема будет взламываться за сутки [8].

Эта проблема широко известна, поэтому сейчас активно разрабатываются алгоритмы, способные противостоять квантовым компьютерам. С 2016 года Национальный Институт Стандартов и Технологий США (NIST) проводил конкурсы на создание первых криптографических методов, устойчивых к атакам квантовых компьютеров. В 2022 года были анонсированы четыре посквантовых криптографических алгоритма [9].

Литература:

1. SSL Report // SSL Labs. URL: https://www.ssllabs.com/ssltest/analyze.html?d=www.gosuslugi.ru (дата обращения 29.04.2023).
2. Breaking RSA Encryption — an Update on the State-of-the-Art // QuintessenceLabs URL: https://www.quintessencelabs.com/blog/breaking-rsa-encryption-update-state-art (дата обращения 29.04.2023).
3. P. W. Shor. Algorithms for quantum computation: discrete logarithms and factoring // Annual Symposium on Foundations of Computer Science. — 1994. — № 35. — С. 124–134.
4. Алгоритм Евклида // Науколандия URL: https://scienceland.info/algebra8/euclid-algorithm (дата обращения 29.04.2023).
5. Quantum Computers, Explained With Quantum Physics/ https://youtu.be/jHoEjvuPoB8 (дата обращения: 07.05.2023).
6. What is post-quantum cryptography // Quantum Strategy Institute URL: https://quantumstrategyinstitute.com/2023/02/15/what-is-post-quantum-cryptography/ (дата обращения 03.05.2023).
7. Quantum Fourier Transform // Qiskit URL: https://learn.qiskit.org/course/ch-algorithms/quantum-fourier-transform (дата обращения: 07.05.2023).
8. 2021 Quantum Threat Timeline Report: Global Risk Institute // Global Risk Instisute URL: https://globalriskinstitute.org/publication/2021-quantum-threat-timeline-report-global-risk-institute-global-risk-institute/ (дата обращения 11.05.2023).
9. NIST Announces First Four Quantum-Resistant Cryptographic Algorithms // NIST URL: 8. https://www.nist.gov/news-events/news/2022/07/nist-announces-first-four-quantum-resistant-cryptographic-algorithms (дата обращения 30.04.2023).