Доплеровская фильтрация сигналов является одной из ключевых операций решаемых устройств приема и обработки радиолокационных сигналов, от правильного выбора параметров которой зависит обеспечение требуемых вероятностных характеристик обнаружения целей.

Доплеровская фильтрация решает следующие задачи:

1) Оценка скорости цели желательно однозначная

2) Повышение качественных характеристик РЛС за счет когерентного накопления узкополосных фильтров

3) Подавление пассивных помех

Самая распространенный способ доплеровской фильтрации — это непосредственное дискретное преобразование Фурье (ДПФ) [3, с. 63]. ДПФ конечной последовательности определяется как

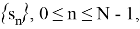
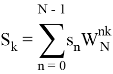
где аргумент функции

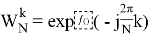
Но также существует быстрое преобразование Фурье (БПФ) [3, с. 145]. Один из классических вариантов — это алгоритм БПФ с прореживанием во времени. Прореживание по времени заключается в разделении исходной последовательности , на две последовательности половиной длительности с четными индексами и с нечетными индексами где , таким образом, что:

, а

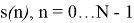
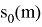
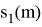
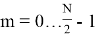
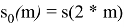
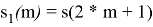
Ниже на рисунке 1 представлено как выглядит прореживание по времени для

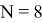
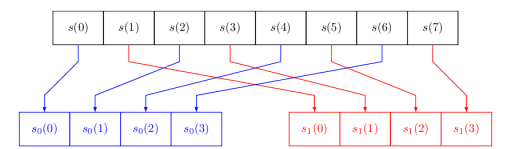
Рис. 1. Прореживание по времени для

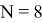
Выражения объединяют два — точечных ДПФ и .

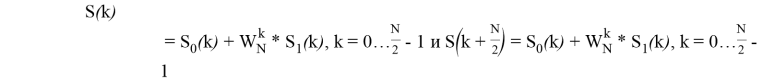
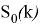
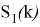
Рисунок 2 иллюстрирует процесс объединения двух ДПФ

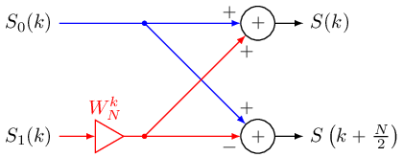
Рис. 1. Граф «бабочка» для БПФ с прореживанием по времени

Также существуют эффективные алгоритмы вычисления ДПФ составной длины. Алгоритм Винограда является одним из таких эффективных алгоритмов доплеровской фильтрации сигналов, который позволяет существенно до 80 % сократить число операций по сравнению с тем же алгоритмом Кули — Тьюки по основанию 2. Но этот алгоритм чрезвычайно сложный из — за своей исключительно нерегулярной структуры вычислений, из — за чего его довольно редко применяют на практике. Обычно на практике применяют его облегченный аналог вычисления БПФ — это алгоритм Гуда — Томаса [1, с. 141].

Алгоритм Гуда — Томаса это есть способ, с помощью которого отображают линейную последовательность из целых чисел в двумерную таблицу преобразующего одномерное преобразование Фурье в двумерное преобразование Фурье. Но сама последовательность должна состоять из взаимно простых чисел. На основе китайской теоремы об остатках определяется способ, с помощью которого переупорядочивается входная и выходная последовательность.

Перестановки входных индексов следует определять по следующему правилу:

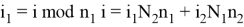
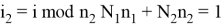
Перестановки выходных индексов следует определять по следующему правилу:

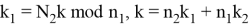
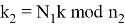
Выражение для вычисления преобразования Фурье имеет вид:

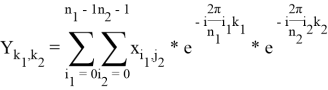
в котором задаются — точечное и — точечные преобразования Фурье.

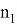
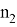
Проиллюстрируем зависимость числа операций от различной реализации алгоритма БПФ на рисунке 3.

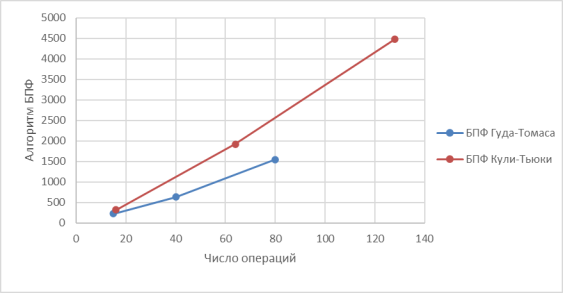
Рис. 3. Зависимость числа операций от вариации алгоритма БПФ.

Литература:

1. Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов: Пер. с англ. — М.: Мир, 1989. — 448 с., ил.
2. Сколник М. Справочник по радиолокации: Пер. с англ. под общей ред. К. Н. Трофимова. Том 1.
3. Лайонс Р. Цифровая обработка сигналов: Второе издание. Пер. с англ. — М.: ООО «Бином-Пресс», 2006 г. — 656 с.: ил.