В статье рассмотрены основные вопросы обучения решению задач с параметрами. Проанализированы УМК на предмет задач с параметрами. Рассмотрены основные типы и способы решения задач с параметрами.
Ключевые слова: задачи с параметрами, типы задач с параметрами, способы решения задач с параметрами.
Решение задач с параметрами при изучении темы помогает учащимся лучше и на более глубоком уровне закрепить изученный материал. Решение задач с параметрами способствует развитию логического мышления, математической культуры и интереса к математике. Задачи с параметрами являются задачами исследовательского типа, так как представляют собой нестандартные задачи, требующие от учащегося анализа, самостоятельного выбора способа действий и применения материала на более глубоком уровне. Современное математическое образование в школе направлено на обучение решению набора стандартных задач. Для решения задач с параметрами недостаточно механического применения изученных формул, алгоритмов и способов их применения. Чтобы решить такую задачу, учащимся необходимо понимание закономерностей, навыки анализа каждого конкретного случая на основе известных общих свойств объекта, системность и последовательность в решении, умение объединить рассматриваемые частные случаи в единый результат.
Задач с параметрами в существующих учебниках по математике мало несмотря на то, что в заданиях выпускных и вступительных экзаменов одной из задачей является задача с параметром. В последнее время в учебной и методической литературе наряду с основными содержательными линиями («Числа и вычисления», «Выражения и их преобразования», «Уравнения», «Функции», «Геометрические фигуры. Измерение геометрических величин») стали выделять линию задач с параметрами.
Задания с параметрами входят в часть 2 с развернутым ответом Основного государственного экзамена (22 задача ОГЭ 2021 года), а также во 2 часть Единого государственного экзамена по математике профильного уровня (18 задача ЕГЭ 2021 года). Экзамен по математике является обязательным для выпускников школ как после 9 класса, так и после 11. Как показывает практика, малое количество экзаменуемых справляется с данными задачами по ряду причин, одной из которых является недостаточное количество времени, уделяемое на уроках решению данных задач. Другой немаловажной причиной является то, что в школьных учебниках или практически отсутствует система заданий с параметрами, или таких заданий недостаточно для того, чтобы учащиеся научились решать задачи с параметром. Также школьной программой не предусматривается время на решение логических задач, что усложняет учащимся решение задач с параметрами, так как они при виде таких задач начинают действовать механически. Но основной проблемой является нехватка времени на изучение данного типа задач непосредственно на уроках.
На период обучения в средних и старших классах школы в подростковом возрасте происходит развитие познавательных процессов, основной характеристикой которых является становление сложных форм аналитической деятельности, переходом к абстрактному, теоретическому мышлению, развитием гипотетических и дедуктивных форм мышления, возможностью строить умозаключения, что важно для успешного решения задачи с параметром 1 .
Задачи с параметрами невозможно научиться решать за один или два урока, поэтому методически правильно уделять время на решение задач с параметрами на уроках обобщения и систематизации, начиная с темы «Линейные уравнения» на уроках алгебры в 7 классе. В УМК А. Г. Мерзляка элементарные задачи с параметрами предлагаются для решения обучающимся уже в 5 классе. Автор таким образом постепенно знакомит детей с понятием параметра на раннем этапе обучения, что дает преимущество данному УМК. При решении задач с параметрами необходимо обратить внимание учащихся на различие между параметром и переменной. Параметр — это какое-то зафиксированное число, в отличие от переменной.
Задачи с параметрами делятся на четыре основных типа 3 :
- Задачи, которые необходимо решить уравнение, неравенство или их системы либо для любого значения параметра, либо для значений параметра, принадлежащих какому-либо множеству (например, необходимо для каждого значения параметра решить квадратное уравнение, либо решения одного уравнения совпадают с решениями другого уравнения).
- Задачи, в которых нужно определить количество решений уравнения, неравенства или их систем в зависимости от значения параметра.
- Задачи, в которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства или их системы и совокупности имеют заданное количество решений (например, дано квадратное уравнение и требуется найти значения параметра, при которых уравнение не имеет решений, имеет одно решение или два решения).
- Задачи, в которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения уравнения, неравенства или их системы (например, дано линейное уравнение с параметром и необходимо найти значения параметра, при котором корень уравнения будет делиться на 3).
Самые распространенные задачи — это задачи с одной переменной и одним параметром.
Большая часть задач с параметрами, которые могут встретиться учащимся на выпускном или вступительном экзамене, принадлежат одному из четырех рассмотренных типов.
Выделяют три основных способа решения задач с параметрами [3]:
- Аналитический. При решении данным способом повторяются стандартные шаги решения уравнения, неравенства или системы без параметра.
- Графический. В зависимости от задачи рассматриваются графики в координатной плоскости.
- Решение относительно параметра. При решении данным способом переменные x и a принимаются равноправными, далее выбирается та переменная, относительно которой аналитический способ решения проще.
Задачи с параметрами необходимо давать учащимся после прорешивания дидактических задач на закрепление материала, что позволит, во-первых, более глубокому усвоению темы, во-вторых, развитие интереса к математике, в-третьих, покажет наличие нестандартных, интересных задач.
В каждой задаче с параметром есть основная идея, на основе которой решается данная задача. Рассмотрим на примере задания для 8 класса.
Пример. При каком значении b имеет единственный корень уравнение 2x^2+4x-b=0?
Учащимся необходимо вспомнить, что значение дискриминанта показывает количество корней квадратного уравнение. Единственный корень уравнение будет иметь, если дискриминант равен 0. Тогда, чтобы ответить на вопрос задачи, необходимо посчитать дискриминант и приравнять к 0.
D=16–8b
16–8b=0
Получилось простое линейное уравнение, из которого легко получим, что b=0.
Ответ: b=0.
Таким образом, основная идея этой задачи — смысл дискриминанта. И чтобы ее решить, детям необходимо знать, при каком значении дискриминанта сколько корней будет.
Рассмотрим пример из параграфа 2.2 реального ЕГЭ по математике 2021 года.
Чтобы решить задачу, нам надо было разложить на множители, что как раз является основной идеей задачи. То есть, прежде чем переходить к решению данного номера, необходимо вспомнить с детьми решение уравнений с помощью разложения на множители и, соответственно, сами способы разложения на множители.
Таким образом, мы предлагаем выделить из задачи основную идею решения, прорешать задачи базового уровня, чтобы вспомнить необходимую теорию, затем решить задачу с параметром более легкого уровня, постепенно усложняя. Таким образом, мы плавно, опираясь на возрастные особенности обучающихся и следуя принципу «от простого к сложному», разбираем с детьми задачи с параметром.
Пример . При каких значениях параметра a уравнение
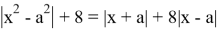
Имеет два положительных корня?
Решение:
Разложим по формуле разность квадратов и соберем все слагаемые с левой стороны:
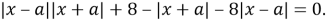
Сгруппируем:
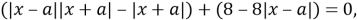
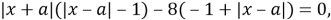
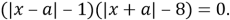
Перейдем к совокупности:
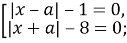
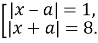
Используя определение модуля, мы сделаем вывод, что:
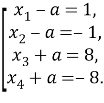
Корни уравнения будут равны:
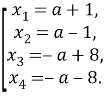
Сделаем предположение, что корни попарно равны, т. е.:
1) если
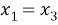
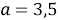
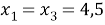
2) если
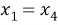
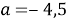
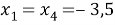
3) если
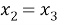
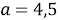
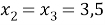
4) если
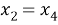
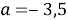
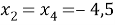
Нам нужно, чтобы корни были положительные. Посмотрим, при каких значения параметра a каждый корень будет положителен.
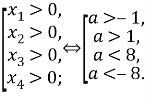
Отметим значения а на числовой прямой, не забывая
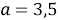
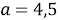
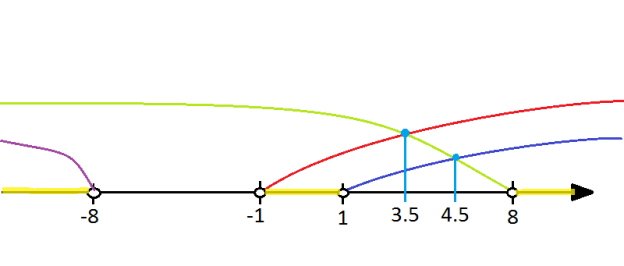
Рис. 1. Значения a на числовой прямой
Обратим внимание, что при
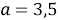
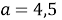
Таким образом, запишем ответ.
Ответ:
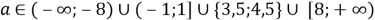
Литература:
- Аверин В. А. Психология детей и подростков: Учёб. пособие. — 2-е изд., перераб. -СПб.: Изд-во Михайлова В. А., 1998. — 379 с.
- Горбачев В. И. Элементы теории и общие методы решения уравнений и неравенств с параметрами [Текст] / В. И. Горбачев; м-во общ. и проф. образования РФ. Брян. гос. пед. ун-т им. акад. И. Г. Петровского. — Брянск: Изд-во Брян. гос. пед. ун-та им. акад. И. Г. Петровского, 1998. — 262 с.
- «Линия задач с параметром в школьном курсе математики» https://cyberleninka.ru/article/n/liniya-zadach-s-parametrami-v-shkolnom-kurse-matematiki/viewer (дата обращения: 08.04.2021)

