В данной работе получены теоремы о кратной полноте и полноте части собственных функций (СФ) для задачи о нормальных колебаниях идеальной релаксирующей жидкости в неподвижном упругом сосуде. Отметим, что в работах [1, 2] исследована структура спектра для некоторых задач о нормальных колебаниях идеальной сжимаемой жидкости во вращающихся сосудах. Рассмотрены случаи, когда сосуд, заполненный жидкостью, представляет собой твёрдое тело упругое или упругую оболочку. Когда же вращения сосуда нет [3], то непрерывный спектр исчезает и остаётся лишь дискретный спектр, для которого естественным образом возникает задача о полноте (СФ). В работе [4] исследована спектральная задача о нормальных колебаниях вращающейся идеальной релаксирующей жидкости в контейнере. Исследованы вопросы локализации, дискретности и асимптотики спектра. Доказаны утверждения о двукратной полноте для системы собственных и присоединённых элементов.
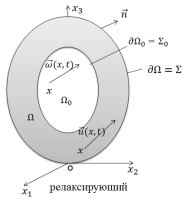
Пусть в сосуде занимающей область Ω ⊂ℝ
3
находится идеальная релаксирующая неоднородная жидкость, полностью заполняющая область Ω0⊂Ω. Обозначим через
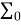
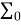
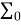
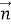
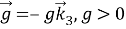
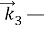
Обозначим через
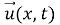
Предполагаем, что упругое тело изотропно, поэтому тензор напряжения этого тела имеет вид
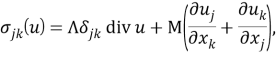
где
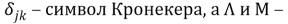
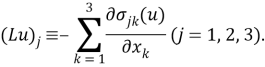
Уравнения малых (линейных) движений этой механической системы с учетом уравнения состояния жидкости записываются в виде (см. [4]):
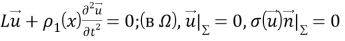
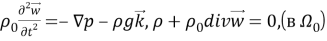
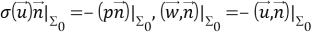
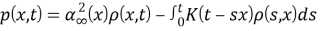
Релаксирующая жидкость моделируется (4) дополнительным уравнением состояния, связывающим динамическое давление p(x,t) и динамическую плотность ρ(х,t), где положительная функция
К(t,х)
определяет ядро интегрального оператора Вольтерра, а
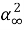
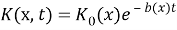
Где К 0 (х) и b(x) положительные функции в области Ω.
Задача о малых движениях идеальной релаксирующей жидкости в упругом теле, заключается в отыскание полей
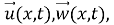
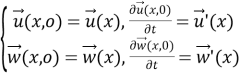
Подобная задача на неподвижном контейнере (при отсутствии силы тяжести и при некоторых модельных ограничениях на граничные условия для динамической плотности) исследовались в [3, с. 390–410]. В работе [4] рассматривалась аналогичная задача при условии, когда действуют гравитационные силы. В отличие от указанных работ, мы рассматриваем релаксирующую жидкость в неподвижном упругом сосуде.
Для этой задачи исследованы вопросы локализации, дискретности и асимптотики спекраю. Доказаны теорема о двухкратной полноте для системы собственных и присоединенных элементов, получено утверждение о существенном спектре задачи.
Литература:
1. Гараджаев А. // Дифференц. уравнения. 1987. Т. 23, № 1. С. 38–47
2. Гараджаев А. // Докл. АН СССР. 1983. Т. 269, № 2. С. 273–278
3. Kopachevcky N. D. Operator Approach to Linear Problems of Hydrodinamics. Vol.2: Nonself-adjoinz Problems for Viscous Fluids-Bessel-Bosson-Berlin: BirkhauserVerlag, 2003–444 p.
4. Закора Д. А. Задача о малых движениях идеальной релаксирующей жидкости, заполняющей вращающееся упругое тело // Динамические системы. — 2006. — Вып.20. — с.104–112.

