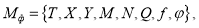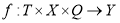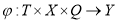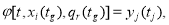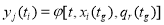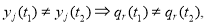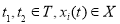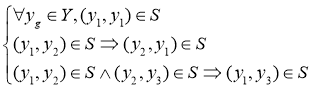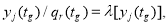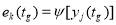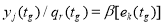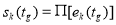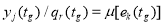В статье проведен анализ моделей функционирования программируемых логических интегральных схем автономного технического средства, выделены основные этапы процесса моделирования при решении задачи технического диагностирования.
Ключевые слова: программируемая логическая интегральная схема, техническое диагностирование, техническое состояние, моделирование, модель функционирования.
При разработке и реализации алгоритмов анализа и диагностирования программируемых логических интегральных схем (далее — ПЛИС) автономного технического средства (далее — АТС) уровень достигаемых характеристик системы технического диагностирования в целом зависит от вида используемой модели функционирования объекта диагностирования. В общем виде различают вербальные, физические и математические модели объекта диагностирования [1].
При использовании физических моделей в качестве эталона применяется заведомо исправный объект диагностирования, идентичный проверяемому.
В этом случае предусмотренные алгоритмом диагностирования управляющие воздействия подаются одновременно на проверяемый и эталонный объект диагностирования, а затем значения телеметрируемых параметров (далее — ТМП) объекта диагностирования сравниваются со значениями ТМП эталонного объекта диагностирования. В случае рассогласований значений ТМП, превышающих заданные допуски, для данной модели характерен ряд существенных недостатков, ограничивающих их применение [1]:
возможность возникновения неисправностей в эталонном объекте и, как следствие, необходимость организации его диагностирования;
низкая экономичность контроля, связанная с высокой стоимостью модели, большими эксплуатационными расходами и т. д.;
необходимость разработки специальных моделей для оптимизации алгоритмов диагностирования, локализации дефектов;
ограничение возможности коррекции модели при совершенствовании моделируемого объекта.
В настоящее время довольно широко используются вербальные модели функционирования объекта диагностирования. При этом информация об эталонном изменении ТМП при выдаче управляющих воздействий содержится в эксплуатационно-технической документации в описательном, слабо формализованном виде. Вербальная форма представления модели объекта диагностирования значительно затрудняет построение формальных процедур. Данному виду моделей присущи следующие недостатки:
отсутствие формальных математических методов синтеза вербальных моделей, проверки их полноты и корректности;
интуитивный, эвристический характер методов построения алгоритмов диагностирования на основе вербальных моделей;
неприспособленность вербальных моделей к использованию в автоматических системах диагностирования;
малая оперативность технического диагностирования.
В свою очередь, увеличение сложности вычислительных систем привело к тому, что использование вербальных и физических моделей для решения задач технического диагностирования, с учетом обозначенных недостатков, становится не актуальным.
Формализация процессов функционирования на основе различных математических моделей позволяет устранить недостатки свойственные для вербальных и физических моделей. Суть диагностирования объекта с использованием математической модели можно свести к сравнению состояний объекта диагностирования и его модели после отработки каждого управляющего воздействия в соответствии с алгоритмом диагностирования. При выдаче очередного воздействия на проверяемый объект диагностирования соответственно изменяется состояние модели. Решение об исправности (работоспособности) объекта диагностирования принимается в случае отсутствия рассогласований состояний модели и ПЛИС при отработке всего алгоритма диагностирования. Системы технического диагностирования с использованием математических моделей объекта диагностирования имеют ряд несомненных достоинств, к числу которых относятся [2, 3]:
возможность разработки формальных методов проверки полноты и корректности используемой модели функционирования объекта;
существование строгих математических методов синтеза оптимизированных алгоритмов технического диагностирования;
широкие возможности повышения уровня автоматизации разработки и реализации алгоритмов технического диагностирования;
повышение оперативности проверки бортовых систем при обеспечении заданного уровня достоверности.
В общепринятом представлении задача контроля и технического диагностирования кажется весьма ясной и прозрачной — определить техническое состояние диагностируемой системы и установить место дефекта в ней с требуемой глубиной в случае возникновения неисправностей (сбоев). Однако, оказывается весьма трудным, а иногда и невозможным, сформулировать эту задачу в числовом виде и выразить ее цель в терминах точно определенной в математическом смысле целевой функции. Здесь, как известно, невозможно найти алгоритмическое решение задачи. Обусловлено это тем, что задача контроля и технического диагностирования относится к классу трудно формализуемых задач, которые характеризуются следующими особенностями [3]:
неопределенностью, ошибочностью, неоднозначностью, неполнотой, противоречивостью и нечеткостью исходных данных и знаний о состоянии системы;
высокой размерностью пространства решений, то есть поиск решения сопряжен с весьма большим перебором возможных вариантов;
значительной динамичностью изменения данных и знаний.
Обширный опыт создания моделей поведения различных объектов, изучаемых в различных теориях, был обобщен в рамках общей теории систем, которая имеет междисциплинарный характер. Результатом этого обобщения явилась некоторая модель, получившая название динамической системы. Поскольку она обобщает многие модели специального вида, то ее можно рассматривать как метамодель, определяющую структуру многих специальных моделей. Динамическая система является довольно сложным математическим понятием, позволяющим с весьма общих позиций рассмотреть облик тех моделей, которые могут быть получены в результате анализа априорных данных из различных источников. В общем виде динамическая система, может быть представлена в виде следующей математической конструкции [4]:
|
|
(1) |
где
М , N — множество мгновенных входных и выходных ситуаций соответственно;
X , Y — множество допустимых входных и выходных ситуаций соответственно;
f — функция переходов, отражающий механизм изменения объекта под действием внутренних и внешних возмущений, которая реализует отображение:
|
|
(2) |
φ — функция выходов, описывающий механизм формирования выходного сигнала как реакции объекта на внутренние и внешние возмущения:
|
|
(3) |
Понятие динамической системы, как оно было определено выше, является достаточно общим, чтобы выработать общую терминологию и увидеть единство в разнообразии более конкретных моделей. Однако на практике наиболее изучены свойства некоторых специальных видов динамических систем, с одной стороны, они проще в изучении, а с другой — они достаточно хорошо описывают многие реальные объекты. К таким видам относят вероятностные, стационарные, а также дискретные и непрерывные динамические системы.
В общем виде динамические системы и различные их подклассы допускают широкий спектр возможных представлений, использующих различный математический аппарат. Каждый из возможных формализмов характеризуется своей техникой и отражает определенную точку зрения на предметную область применительно к которой он применяется.
Ранее было показано, что в общем случае задачу определения исправности ПЛИС можно рассматривать с позиции парадигмы технического диагностирования, а значит, можно интерпретировать как задачу определения вида технического состояния, то есть состояние ПЛИС, при котором расхождение в классах эквивалентности выходных последовательностей относится к классу неисправных состояний. Данное утверждение можно пояснить следующим образом: из литературы [5] известно, что техническое состояние объекта — это состояние, которое характеризуется в определенный момент, при определенных условиях внешней среды, значениями параметров, установленных технической документации.
В свою очередь, контроль технического состояния — проверка соответствия значений параметров объекта требованиям технической документации и определения на этой основе одного из заданных видов технического состояния в данный момент времени. В данном случае возникает задача достоверного распознавания системой диагностирования ошибки в работе ПЛИС.
В основе работы системы диагностирования положено программно-алгоритмическое обеспечение, которое разрабатывается с учетом специального математического обеспечения (далее — СМО). Ключевым положением последнего является модель функционирования объекта технического диагностирования [6].
На рис. 1 представлена обобщенная схема разработки СМО системы технического диагностирования ПЛИС с учетом решаемых диагностических задач.
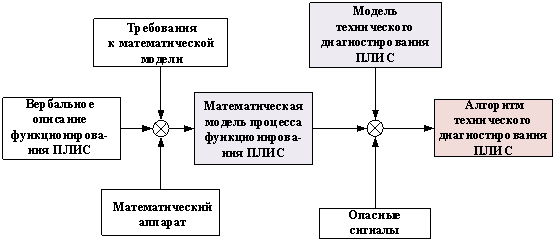
Рис. 1. Обобщенная схема разработки специального математического обеспечения системы технического диагностирования ПЛИС
С учетом требований к математической модели, вербального описания функционирования ПЛИС и с учетом выбранного математического аппарата строится (определяются параметры) математическая модель процесса функционирования ПЛИС. Полученная модель, модель технического диагностирования и опасные сигналы являются основой формирования (разработки) алгоритма технического диагностирования ПЛИС. Следовательно, в состав СМО должны входить полученная математическая модель и алгоритм технического диагностирования ПЛИС.
Необходимо отметить, что определение математического аппарата на данном этапе является несущественным, в связи с этим под математическим аппаратом будем понимать «инструмент» для формализации процесса функционирования в общем. Исходя из обозначенного, постановка задачи разработки математической модели функционирования ПЛИС может быть представлена следующим образом:
-
Вербальное описание моделируемой системы, позволяющее формализовать процесс функционирования ПЛИС, в котором отражены наборы базисных множеств
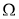
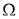
- Математический аппарат I , применяемый для формализации процесса функционирования ПЛИС. Как было отмечено ранее, на данном этапе определение конкретного аппарата является несущественным, в связи с этим под I будем понимать «инструмент» для формализации в общем.
-
Математическая модель процесса функционирования ПЛИС, которая с формальной точки зрения может быть представлена как
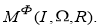
Таким образом, требуется разработать модель анализа технического состояния
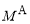
Для разработки математической модели анализа технического состояния ПЛИС с учетом дополнительной диагностической информации воспользуемся подходом, в основе которого лежат абстрактные элементы из теории категорий и системного представления задачи анализа технического состояния в целом. Необходимо отметить, что предлагаемый подход схож по своему смыслу с так называемым унифицированным языком моделирования, в зарубежной литературе данный подход на называется UML (Unified Modeling Language) [6]. Ключевой особенностью данного способа является возможность так называемого метамоделирования, построенного на представлении исследуемых процессов с позиции многоуровневой иерархии по видам математической абстракции. На рис. 2 представлена обобщенная схема к разработке математической модели анализа технического состояния ПЛИС.

Рис. 2. Обобщенная схема подхода к разработке специального математического обеспечения системы технического диагностирования ПЛИС
Из литературы [7] известно, что процесс технического диагностирования ПЛИС, как динамической системы заключается в реализации двух этапов. На первом этапе производится достаточно большое число экспериментов, связанных с имитацией различных состояний объекта в лабораторных или натурных условиях, то есть решается задача идентификации, построения модели функционирования ПЛИС по входным и выходным экспериментальным данным. Второй этап заключается в определении реального технического состояния объекта контроля по результатам выполненных измерений, принятых в качестве эталонных, модельных (результат первого этапа). В совокупности все этапы представляются следующей обобщенной диаграммой, полученной от объединения отображений [5, 6] (Рис. 3).
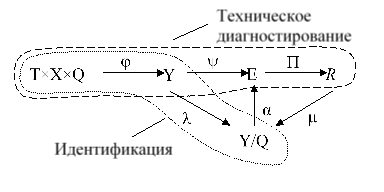
Рис. 3. Модель процессов технического диагностирования ПЛИС
Здесь:
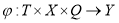
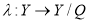
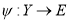
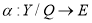
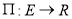
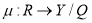
Данная модель может быть представлена в операторной форме. С этой точки зрения процесс определения ТС также можно разделить на несколько этапов. Результатом первого этапа является определение операторного уравнения наблюдения относительно
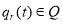
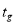
|
|
(4) |
где
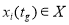
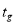
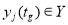
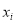
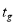
Необходимо также отметить, что уравнение (4) строится на основе функции выхода
|
|
(5) |
при соблюдении условия наблюдаемости, необходимым и достаточным условием которого является инъективность отображения (функция выхода):
|
|
(6) |
|
|
Благодаря этому выходные переменные можно использовать в качестве признаков наблюдаемого текущего состояния объекта.
Итак, первым этапом при реализации процесса определения технического состояния объекта является решение задачи наблюдения, то есть решения уравнения (4).
При полной наблюдаемости объекта всегда возможно определение его состояния по данным измерений сигналов на его выходах. Но конечной целью диагностирования является определение одного из заданных видов технического состояния, к которому может быть отнесено наблюдаемое текущее состояние объекта. Задача отнесения наблюдаемого состояния объекта к одному из заданных видов его технического состояния называется задачей классификации, решение которой можно отнести ко второму этапу процесса технического диагностирования. Однако решению данной задачи должно предшествовать определение классов эквивалентности на множестве выходных параметров, обладающих следующими свойствами [2, 4]:
|
|
– свойство рефлексивности; — свойство симметричности; — свойство транзитивности |
(7) |
где S — бинарное отношение эквивалентности на множестве Y .
Отношение эквивалентности задает разбиение множества Y всех состояний объекта на непересекающиеся классы, то есть осуществляет факторизацию этого множества. Обозначим получающийся при этом класс на основе оператора λ , через следующее выражение:
|
|
(8) |
где
λ
— оператор, соответствующий отображению
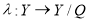
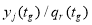
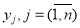
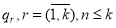
Как было отмечено ранее, целью диагностирования является определение одного из видов технического состояния, к которому может быть отнесено наблюдаемое текущее состояние объекта. С математической точки зрения данное выражение может быть определено через оператор ψ в следующем виде:
|
|
(9) |
Тогда с учетом выражения (9) и по существу рассматриваемой задачи необходимо, чтобы элемент множества
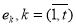
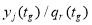
|
|
(10) |
С точки зрения теории множеств отображение, реализуемое посредством оператора (10) будет находиться во взаимно однозначной зависимости, если отображение реализуемое оператором (8) будет являться естественным отображением, а отображение реализуемое оператором (9) будет являться наложением (сюрьекцией), то есть элемент
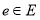
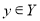
Оператор
ψ
сопоставляет набору
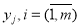
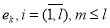
На завершающем этапе определения технического состояния объекта происходит реализация отображения конкретного решения, реализуемого на основе оператора П , который формально определенному виду технического состояния, в рамках заданной модели, ставит в соответствие вполне конкретное решение об его истинном техническом состоянии с учетом вероятностных характеристик, возможных ошибок при техническом диагностировании (в частности, ошибок 1-го и 2-го рода), погрешностей выполняемых измерений и помех:
|
|
(11) |
Также, необходимо отметить, что с целью уточнения математической модели бортовой аппаратуры возможна реализация отображение, представляемое оператором µ в выражении:
|
|
(12) |
которое позволяет провести уточнение сформированного в результате решения задачи классификации выражения
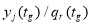
Литература:
- Микони С. В. Квалиметрия моделей и полимодельных комплексов: монография. — М.: РАН, 2018.
- Охтилев М. Ю. Теоретические и технологические основы концепции проактивного мониторинга и управления сложными объектами — Известия ЮФУ. Технические науки, 2015.
- Рудаков В. Б. Математические модели надежности космических аппаратов радиоэлектронной аппаратуры негерметичного исполнения. Известия высших учебных заведений. — СПб.: ИТМО, 2018.
- Manzoor S. Neural Oscillator Based CPG for Various Rhythmic Motions of Modular Snake Robot with Active Joints — Intell Robot Syst, 2019.
- Лоскутов А. И. Идентификация и техническое диагностирование бортовой аппаратуры автономных космических аппаратов на основе биективного преобразования множества диагностических признаков — Контроль диагностика, 2016.
- Лоскутов А. И. Полимодельный подход в задаче технического диагностирования бортовой радиоэлектронной аппаратуры космических аппаратов — Информационно-экономические аспекты стандартизации и технического регулирования: Научный интернет-журнал, 2017.