Статья посвящена проблеме проведения урока физики на тему центростремительное движение и объяснения ученикам центростремительного ускорения в общеобразовательных учебных заведениях.
Ключевые слова: вектор, предельный переход, ускорение, мгновенная скорость, центростремительное ускорение.
Очень часто преподавателю физики приходится ломать голову над объяснением материала, который требует наличия у учеников необходимых математических знаний и навыков. Ярким примером этому могут служить такие понятия, как вектор, лимит, предельный переход, производные и т. д.
Конечно, в любом классе найдутся ученики, которые хорошо владеют математическим аппаратом, но как быть с остальными? В таких случаях приходится идти другим путем и использовать более понятный для учеников язык. К примеру, если введение и объяснение понятия ускорение и не составляет для учителя больших проблем, то с объяснением центростремительного ускорения дело обстоит несколько хуже.





Во всех этих случаях тела или частицы тел отлетают со скоростью, которую они имели в момент отрыва [2].
Хотя вращение тел и происходит с постоянной скоростью, то есть, даже если модуль скорости и не меняется, вращательное движение является переменным, то есть, имеет ускорение. И наиболее трудным для учеников в данной теме является правильное восприятие и понимание направления и значения центростремительного ускорения — a n . Эта трудность связана главным образом с использованием таких сложных для понимания учеников понятий, как вычитание векторов и предельный переход.
Для объяснения центростремительного ускорения, необходимо будет освежить знания учеников по операциям над векторами. Пусть скорость тела в точке А равен вектору v 1 . При перемещении в точку В за время Δt, скорость тела изменится на вектор v 2 . Согласно правилу вычитания векторов, изменение вектора скорости будет равен вектору Δ v . Из рисунка 1 видно, что для очень маленького промежутка времени, то есть при Δt →0, этот вектор направлен радиально в центр окружности. При этом, элементарное перемещение ΔS стремится к длине дуги окружности АВ, которая в свою очередь равна v 1 Δt .
Из подобия треугольников АВО и ACD следует, что
Δv/v 1 = АВ/R .
Но так как АВ = v 1 Δt , то можно писать, что
Δv/v 1 = v 1 Δt /R, или Δv/Δt = v 1 2 /R.
Это изменение скорости за промежуток времени Δt и называется центростремительным (или нормальным) ускорением, так как он всегда направлен в центр окружности, то есть,
a n = v 2 /R .
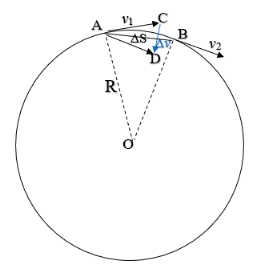
Рис. 1.
Можно еще упростить задачу и выразить изменение скорости Δ v следующим образом. На рисунке 2 угол φ определяется отношением длины дуги АВ к радиусу АО.
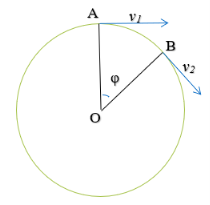
Рис. 2.
Для лучшего понимания, треугольник из векторов скорости потребуется показать отдельно, как на рисунке 3:
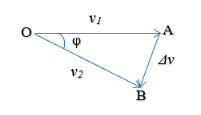
Рис. 3.
Для малых углов, то есть для малых промежутков времени Δt, длина дуги почти не отличается от хорды АВ (рисунок 3). Следовательно, можем писать:
Δφ = Δv/v 1 ,
или,
Δv = Δφ*v 1 .
Так как
a = Δv/Δt,
подставив вместо Δv его значение, получим
a = Δφ*v 1 /Δt.
Но изменение угла по времени — есть угловая скорость вращения w . Значит,
a = w v 1 .
И наконец, учитывая, что
w = v/R,
получим:
a = v 2 /R .
Эти два варианта подачи материала принципиально не отличаются друг от друга, и учитель может выбрать любой из них для лучшего объяснения темы [1]. При объяснении центростремительного ускорения необходимо подчеркнуть, что и ускорение в прямолинейном движении и центростремительное ускорение определяются как изменение скорости за определенный промежуток времени, однако, в прямолинейном движении меняется только модуль (значение) скорости, а в равномерном криволинейном — только направление. В первом случае направление ускорения совпадает с направлением скорости, а во втором — направлено перпендикулярно к ней [1].
Литература:
- Методика преподавания физики в средней школе. Л. И. Резников, С. Я. Шамаш, Э. Е. Эвенчик. Москва, «Просвещение», 1974 год.
- Учебник физики для 10-классов. К. А. Турсунметов и др., Ташкент, «Ўқитувчи», 2022 год.

