Основой технологии вложения систем являются новые конструкции матриц, составляемые на базе матрицы коэффициентов исследуемой системы проматрица, репроматрица и матрицы вложения, образ — исчерпывающим образом определяющие характеристики и свойства заданной системы.
Ключевые слова: электроэнергетическая система, статическая устойчивость, технология вложения систем, автоматический регулятор возбуждения.
Технологией вложения систем названа универсальная совокупность методов и приемов решения задач теории систем, основанная, прежде всего, на современных достижениях алгебры и сводящаяся к определению условий, при которых сложно организованная (многомерная, матричная) система ведет себя аналогично относительно более простой (односвязной, заданной, хорошо изученной или доступной для глубокого исследования) системы [1, с. 48]. Сутью технологии вложения систем является формально строгое определение таких условий, при которых поведение сложно организованной матричной системы описывается или интерпретируется поведением совокупности более простых систем.
Уравнения электромагнитных переходных процессов в цепи возбуждения i -ой синхронной машины имеют вид [2, с. 35]:
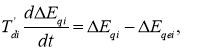
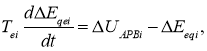
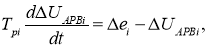
где
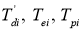
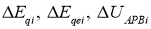
Формирование сигналов по каналам АРВ е i в идеализированном виде (при условии, что постоянные времена дифференцирующих элементов АРВ считаются равными нулю) можно представить в виде [3, с. 268]:
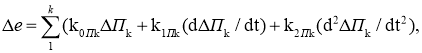
где k 0П k , k 1П k , k 2П k — коэффициенты усиления АРВ по каналам отклонения, первым и вторым производным режимных параметров П k соответственно, k — количество регулируемых параметров режима.
Если не учитывать постоянную времени автоматического регулятора (T pi =0), тогда уравнение выхода автоматического регулятора имеет вид:
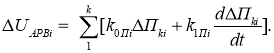
При малых возмущениях параметров режима можно получить обобщенную блочную матрицу А размера (4nx4n) для динамики электроэлектрической системы (ЭЭС) с n генераторами, имеющими АРВ сильного действия в виде:

При этом вектор-столбец параметров состояния, содержащий параметры режима электрической системы, имеет вид:
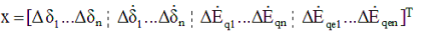
Необходимо отметить, что при выбранной модели АРВ (5) размер обобщенной матрицы A Σ исследуемой электрической системы имеет порядок (4nx4n), где n-количество генераторов ЭЭС.
Рассмотрим формирование обобщенной матрицы входа В . Содержание данной матрицы целиком зависит от закона регулирования возбуждения и, соответственно, параметров каналов автоматического регулирования, по которым осуществляется управление системой возбуждения n синхронных машин, установленных в ЭЭС. Для выбранного закона регулирования возбуждения (5) обобщенная матрица В имеет размер 4nxn(k-m) и вид [6, с. 31–34]:
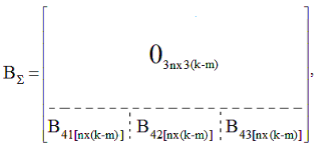
где m-количество параметров режима, входящих в обобщенную матрицу динамики ЭЭС, таких как элементы вектора пространства состояний электрической системы.
Таким образом, обобщенные матрицы А , В позволяют описать переходные процессы в сложной ЭЭС с n генераторами при малых возмущениях параметров режима.
Например, для трехгенераторной ЭЭС при предположении, что АРВ–с реагирует на отклонения напряжения и угла нагрузки генераторов (
i
, U
Гi
), а также их первых производных
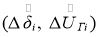
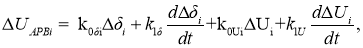
где i=1÷3, и постоянная времени автоматического регулятора не учитываются (T pi =0).
Как указано в [2, с. 37], для квадратной матрицы (m=n и C=I n ) проматрица моделирования для объекта будет иметь вид:
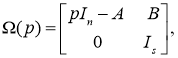
а для регулируемой динамической системы со статическим регулятором:
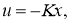
проматрица будет равна:
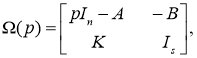
где А, В, С — заданные числовые матрицы, К — матрица коэффициентов регулятора (n — степень математической модели объекта исследуемой системы, m — количество входов системы, s — количество выходов регулятора).
В соответствии с [4, с. 459] технология вложения в скалярный образ
— для разомкнутой системы:
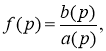
— для замкнутой регулятором системы:
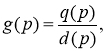
требует формирования детерминантных соотношений, позволяющих решить проблему нахождения матричных числителей:
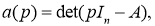
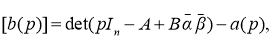
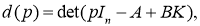
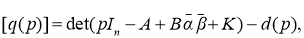
Содержание в системе матричных уравнений следующее: а(р), d(p) — характеристические полиномы для модели исследуемого объекта — электрической системы и замкнутой регулируемой ЭЭС; [b(p)], [q(p)] — соответственно, их матричные числители,
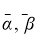
Соотношения (11)-(14), в отличие от одномерного случая, позволяют для многомерного объекта с регулятором найти матричные числители матричных передаточных функций для исследуемой системы, что является характерным для современного подхода исследования сложных динамических систем [5, с. 143].
Следует заметить, что модель электрической системы, представляемая в виде матрицы А , эффективна при исследовании сложных электрических систем, так как она проста и выгодна в вычислительном отношении — состоит из блоков нулевой и единичной матриц и соответственно разрежена. Самое важное: она содержит только информацию об основных параметрах системы, характеризующих устойчивость — углы генераторов и их демпферные коэффициенты, интегрировано отражающие колебательные свойства, как каждого генератора, так и всей системы [6, с. 31–34].
Таким образом, можно отметить, что технология вложения систем позволяет комплексно исследовать переходные режимы исследуемой системы как по отдельным каналам, так и при интегрированном учете влияния существующих каналов.
Литература:
- Литкенс, И.В., Пуго, В. И. Колебательные свойства электрических систем. — М.: Энергоатомиздат, 1988. — 217 с.
- Аллаев, К.Р., Мирзабаев, А.М., Махмудов, Т.Ф., Махкамов, Т. А. Исследования малых колебаний в регулируемой электрической системе методом технологии вложения систем // Проблемы энерго- и ресурсосбережения. — 2015. –№ 1–2. — С. 32–42.
- Веников, В. А. Переходные электромеханические процессы в электрических системах. — М.: Высшая школа, 1985. — 537 c.
- Буков, В. Н. Вложение систем. Аналитический подход к анализу и синтезу матричных систем. — Калуга: Издательство Н. Ф. Бочкаревой, 2006. — 720 с.
- Мисриханов, М. Ш. Инвариантное управление многомерными системами. — М.: Наука, 2007. — 284 с.
- Аллаев К. Р., Махмудов Т. Ф. Исследование статической устойчивости многомашинной электрической системы на основе технологии вложения систем // Материалы VII Международной молодёжной научно-технической конференции «Электроэнергетика глазами молодежи — 2016», Т.2, С. 31–34.

