Исследование марковских моделей обслуживания



Ключевые слова: модель процесса обслуживания, марковских моделей, теории массового обслуживания.

Если рассмотреть моменты времени, когда в систему поступают требования, то множество этих моментов образует поток однородных событий или напрямую цельную меру (мерой любого интервала времени будет число требований, поступивших в систему за этот интервал). Случай, когда поток является определяющим, представляет ограниченный интерес. Важнее рассматривать случайные потоки однородных событий, то есть случайные цельные меры. Ниже мы остановимся на основных результатах, относящихся к потокам однородных событий; здесь же опишем простейшую модель потока (термин «простейший поток» введён А. Я. Хинчиным).

Среди всевозможных распределений длительности обслуживания требований выделяется экспоненциальное распределение; его отличительной особенностью является то, что длительность обслуживания не зависит от t при условии, что к этому моменту обслуживание не закончилось. При простейшем входящем потоке требований и быстро распределённой длительности обслуживания можно построить марковский процесс с ограниченным или числовым множеством состояний, представляющий статистическую модель процесса обслуживания; при этом основные показатели качества обслуживания оказываются функционалами построенного процесса. Указанное обстоятельство имеет место и в более общем случае, а именно, когда поток и обслуживание имеют марковский характер. Визуальный смысл этого понятия состоит в том, что вероятность поступления в систему или окончания обслуживания от t до t+ определяется лишь состоянием системы и не меняется при дополнительной информации о состоянии системы. Иными словами, состояние процесса, как функция времени, образует марковский процесс. Приведём пример марковской модели: процесса обслуживания, где поток требований в общем случае — не простейший, а длительность обслуживания — не экспоненциально-распределённая.

Условия эргодичности теории цепей Маркова в наиболее удобном виде для использования в теории массового обслуживания были выяснены Фостером. Ходжес и Розенблатт исследовали распределение времени возвращения при случайном блуждании. Предельная теорема о распределении времени пребывания в различных состояниях в случае однородного марковского процесса была представлена Сираждиновым.

Для исследования переходных процессов в системах массового обслуживания важно оценивать скорость сходимости переходных вероятностей цепи или процесса к предельным вероятностям.

В недавней работе Вир-Джонса доказана предельная теорема, которая может служить основанием для оценки в применении ко многим конкретным моделям, в том числе немарковским. Вир-Джонс показал, что в большинстве случаев имеет место быстрая сходимость вероятностей перехода цепи Маркова к пределам счётной . Причём, где константа p <1 не зависит от i и j. В большинстве задач теории массового обслуживания математическая модель может быть построена при помощи процесса рождения и гибели, то есть марковского (обычно однородного) процесса со счётным множеством состояний, когда в момент изменения состояния процесса с вероятностью 1 происходит переход в предыдущее или следующее состояние.

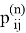
Классификация процессов рождения и гибели осуществлена в работе Карлина и Мак-Грегора. Пусть состояния процесса занумерованы 0, 1, 2,...; пусть далее λ _i — интенсивность перехода из состояния i в состояние i + 1, а µ _i — интенсивность перехода из i в i — 1. Тогда, как показали Карлин и Мак-Грегор, необходимым и достаточным для ошибочности процесса является выполнение следующих двух условий:

Важным методом в теории марковских моделей массового обслуживания является теория ветвления случайных процессов. Этот метод особенно важен для теории надежности, где с его помощью описываются отказы в сложном оборудовании (отказ одного элемента порождает отказы других элементов). Предельные теоремы для важных классов случайных процессов были найдены Б. А. Севастьяновым и В. П. Чистяковым.

Образование предельных теорем для процессов рождения и гибели основывается на различных аналитических предположениях относительно поведения λ _n и µ _n как функций n. Наиболее простая картина получается, когда эти функции линейны при n > 0. Обобщение на тот случай, когда имеется поглощающий экран при n = N, осуществлено в статье Саати. Отметим также интересную работу, посвящённую связи между цепями Маркова и процессами рождения и гибели. Перейдем к изложению результатов, касающихся конкретных моделей систем массового обслуживания.

Система с ожиданием . Предположим, что имеется n обслуживающих приборов, на которые поступают простейшие требования. В случае занятости всех приборов требования становятся в очередь с естественной дисциплиной и ожидают начала обслуживания. Длительность обслуживания распределена по экспоненциальному закону с одинаковыми параметрами для всех приборов. Для подобной системы основной интерес представляет нахождение распределения длины очереди в стационарном режиме, а также распределения длительности ожидания. Эти задачи решены А. Н. Колмогоровым в 1931 г. А. Н. Колмогоров нашел необходимое и достаточное условие существования стационарного распределения рассматриваемых случайных процессов, которое заключается в следующем: среднее число требований, поступающих в систему в единицу времени, должно быть меньше производительности системы, то есть произведения числа приборов. Получено интегральное представление для вероятностей состояний системы (числа находящихся в ней требований) в нестационарном случае по среднему числу требований, которые один прибор может обслуживать в единицу времени. С этой точки зрения следует ряд полезных выводов об асимптотическом поведении указанных вероятностей. В работах Бейли и Лучака получены некоторые точные формулы для нестационарного случая в предположении, что имеется всего один обслуживающий прибор. В частности, исследовано распределение периода занятости прибора и сделан вывод о том, что интенсивность обслуживания и входящего потока может зависеть от времени. Ввиду сложности общего решения зависимости указанных параметров от времени, в некоторых работах ищутся нестационарные распределения для ряда частных случаев. Таким образом, Галлихер и Уилер рассчитали постоянный случай интенсивности обслуживания и входящего потока. Это характерно для ряда систем, в частности, аэродромов с чередующимся графиком работы.

Различают преимущества непрерывающие и прерывающие; во втором случае, в дополнение к сказанному выше, в случае, когда поступает преимущественное требование, обслуживание непреимущественных требований прерывается. Кроме того, различают прерывание с повторением и без повторения, — в зависимости от того, учитывается ли при возобновлении обслуживания время, ранее затраченное обслуживание требования. Поскольку длительность обслуживания распределена по экспоненциальному закону, последние две разновидности приводят к одной и той же статистической модели.

Системы с потерями (отказами). Марковскую модель системы массового обслуживания с потерями впервые исследовал Эрланг, который вывел знаменитые формулы для стационарных вероятностей состояний системы, носящие его имя. Рассмотрение систем с потерями особенно существенно для телефонии; этим объясняется большое число относящихся сюда теоретических и прикладных работ в этой области. Формулы Эрланга несколькими авторами обобщались на более сложные системы с потерями, чем рассмотренные Эрлангом. Таким образом, исследовались двухступенчатые и многоступенчатые системы, соответствующие сложным телефонным сетям. Отметим работу Г. П. Башарина, в которой формулы Эрланга обобщены на случай двухступенчатой системы. Подобные формулы решают задачу формально полностью; однако, в связи с тем, что реальные телефонные сети содержат очень большое число элементов, расчёт по точным формулам становиться весьма затруднительным. Это обстоятельство стимулировало развитие приближенных методов на пути применения предельных теорем теории вероятностей.

Литература:

1. Гурбангулы Бердымухамедов. Государственное регулирование социально-экономического развития Туркменистана: Учебное пособие для высших учебных заведений. — I том. — Ашхабад: Туркменская государственная издательская служба, 2010.
2. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслуживания. — Москва: Наука, 1966. — 432 с.
3. Рыков В. В. Управляемые системы массового обслуживания // Итоги науки и техн. Сер. Теор. вероятн. Мат. стат. Теор. кибернет. — 1975. — Т. 12. — С. 43–153.
4. Назаров А. А., Терпугов А. Ф. Теория массового обслуживания. — Томск: Изд-во НТЛ, 2010. — 238 с.
5. Боровков А. А. Вероятностные процессы в теории массового обслуживания. — Москва: Наука, 1971. — 368 с.
6. Башарин Г. П., Толмачев А. Л. Теория сетей массового обслуживания и ее приложения к анализу информационно-вычислительных систем // Итоги науки и техн. Сер. Теор. вероятн. Мат. стат. Теор. кибернет. — 1983. — Т 21. — С. 1–119.
7. Бочаров А. А., Печинкин А. В. Теория массового обслуживания: Учебник. — Москва: Изд-во РУДН, 1995. — 529 с.