Когерентная Машина Изинга и QUBO-решатели



В статье рассматривается вопрос появления и строения вычислительных машин, предназначенных для решения проблем бинарной оптимизации. Освещается применение Когерентной Машины Изинга как аппаратного средства их реализации и приводятся альтернативные решения.

Ключевые слова: Когерентная Машина Изинга, QUBO-решатель.

The article deals with the issue of the appearance and structure of computers designed to solve problems of binary optimization. The use of the Coherent Ising Machine as a hardware tool for the implementation of QUBO solvers is discussed. The article also provides alternative hardware solutions.

Keywords: Coherent Ising Machine, QUBO solver.

Интерес к области квантовых вычислений, возникший после известной работы Ричарда Фейнмана [1], привел к появлению в последнее время ряда аналоговых симуляторов модели Изинга, на которые могут быть математически отображены известные вычислительные задачи NP сложности.

При решении проблем, связанных с оптимизацией времени вычислений и ускорением работы различных алгоритмов, возникают разные по сложности классы задач:

1) Простейшей категорией из классов сложности является категория проблем разрешимости (decision problems), предполагающая бинарный ответ, «да» или «нет». Если для проблемы разрешимости существует эффективный алгоритм, то проблема относится к классу сложности P (Polynomial timing), что соответствует детерминистическому полиномиальному времени, а алгоритм отождествляется с детерминированной машиной Тьюринга.

2) Второй класс задач — задачи NP — сложности. Если проблема разрешимости такова, что, предложив или обеспечив возможное решение, можно оперативно убедиться, что это решение корректное, тогда проблему относят к классу сложности NP.

3) Третий класс сложности NP, также называют NP-трудный (-hard). Формально говорят, что проблема NP-трудная, если алгоритм для решения такой проблемы может быть эффективно перекодирован в алгоритм для решения любой проблемы в классе NP. Если проблема принадлежит одновременно к классам NP и NP-трудный, ее относят к классу сложности NP-полный (-complete). Грубо говоря, отнесение проблемы к классу NP-полный означает, что с высокой вероятностью не существует эффективного алгоритма для решения примеров в такой проблеме, будь то алгоритм классической или квантовой природы [2].

На настоящий момент самые сложные задачи из класса NP-полный можно решить лишь за экспоненциальное время, что считается неприемлемым с точки зрения вычислений на классическом компьютере. Графическое изображение множеств классов приведено на рис. 1.

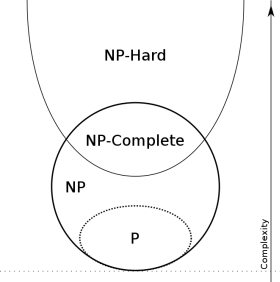
Рис. 1. Иллюстрация множеств P, NP и NP-трудных классов сложности

Таким образом для решения NP задач в настоящее время развиваются различные вычислительные машины и методы нового поколения, в том числе квантовые компьютеры. В частности, машины квантового отжига могут искать минимальное значение функции с высокой скоростью.

Такие компьютеры представляют собой физическую систему, реализующую квантовое моделирование поведения набора из N спинов ½ (двухуровневых систем), которое, по предположению Фейнмана, должно быть более эффективным (быстрым), чем соответствующее классическое моделирование. Действительно, поскольку N спинов могут пребывать в 2 ^N конфигурациях, то вычислительная задача имеет экспоненциальную по N сложность. К таким задачам относится нахождение минимума энергии спинов, которая может быть сведена к проблеме бинарной оптимизации QUBO.

При классическом описании каждый спин может находиться либо в состоянии «вверх», либо в состоянии «вниз». При квантовом описании состояние спина есть кубит — суперпозиция этих двух потенциальных возможностей. На сегодняшний день имеется, несколько подходов к решению задачи оптимизации (нахождения минимума функции энергии) на основе квантовых систем, использующих, с физической точки зрения эффекты квантового туннелирования. На рис. 2 изображена физическая реализация кубита со спином, которая используется при создании симулятора квантового отжига [3].

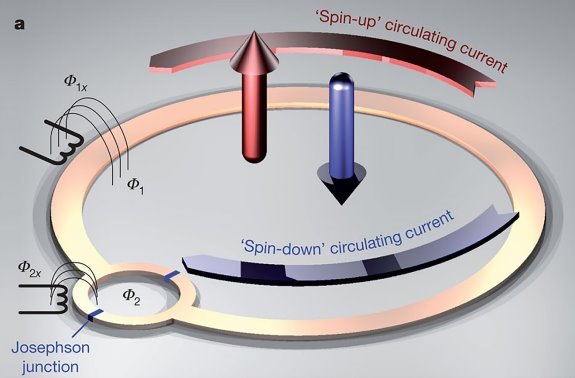
Рис. 2. Упрощенная схема физического кубита, основанная на сверхпроводящем потоке, действующем как квантово-механический спин. Ток, циркулирующий в петле кубита, порождает поток Φ ₁ , кодирующий два различных состояния спина, которые могут существовать в суперпозиции

Вычислительные машины, предназначенные для решения проблем бинарной оптимизации QUBO называются QUBO-решателями. На сегодняшний день доминируют два подхода к созданию такого рода машин: на основе квантовых вентилей (модель квантовых цепей) и на базе квантового отжига (модель адиабатических квантовых вычислений). Эти подходы обычно преподносятся как несвязанные, однако при тщательном изучении можно прийти к выводу, что они могут быть эквивалентны. Тем не менее они заметно отличаются друг от друга, что существенно для получения практического превосходства над классическими компьютерами.

Одним из примеров квантовых аппаратных устройств, предназначенных для решения проблемы бинарной оптимизации QUBO, может служить Когерентная Машина Изинга (CIM). Когерентная машина Изинга — квантовое вычислительное устройство, в котором дискретизированные фазы вырожденных оптических параметрических генераторов (DOPO) используются для моделирования спинов Изинга. В отличие от квантовых отжигов, использующих сверхпроводящие квантовые биты, КМИ может работать при комнатной температуре благодаря использованию высокочастотных оптических генераторов для имитации спинов. В настоящий момент разработана КМИ на 100000 вращений, описанная в работе [4].

Основой КМИ является оптический параметрический генератор DOPO — это оптический генератор, который можно реализовать, поместив фазочувствительный усилитель (PSA) в оптический резонатор. PSA представляет собой оптический усилитель, основанный на оптическом параметрическом усилении и эффективно усиливающий компоненты фазы 0 и π относительно фазы накачки. В результате DOPO принимает значение фазы только 0 или π выше порога колебаний; таким образом, дискретные фазовые состояния можно использовать для представления изинговских спиновых состояний. КМИ, описанный в [4], генерирует тысячи мультиплексированных во времени импульсов DOPO путем включения и выключения PSA, размещенного в 5-километровом оптическом волокне с частотой 1 ГГц (рис. 3). Взаимодействие между импульсами DOPO реализуется с помощью метода, основанного на использовании обратной связи. С помощью этого метода некоторые N импульсов DOPO разделяются с помощью светоделителя для каждого вращения в резонаторе и измеряются амплитуды (со знаками) всех N импульсов DOPO. Результаты измерений вводятся в цифровую схему матричного расчета, где заранее устанавливается матрица спин-спинового взаимодействия (матрица размера N × N) для заданной задачи Изинга. Цифровая схема умножает матрицу и набор N и по результатам измерений позволяет получить сигнал обратной связи для каждого импульса при очередном вращении. Затем мы используем сигнал обратной связи для модуляции оптического импульса, и импульс вводится в соответствующий импульс DOPO внутри резонатора через другой светоделитель для завершения измерения и окончания прохождения круга обратной связи. При повторении этой процедуры обычно в течение 100–1000 вращений в резонаторе комбинация фаз DOPO превращается в фазу, наиболее стабилизирующую всю систему, которая во многих случаях соответствует основному состоянию данного задачи Изинга.

Применение данной вычислительной машины, а также других QUBO-решателей уже нашло применение в таких областях, как:

— Оптимизация производственных процессов [5]

— Оптимизация работы оборудования [6]

— Планирование производства [7]

— Нейросети

— Логистика и грузоперевозки [8]

— Молекулярное моделирование [9]

— Портфельная оптимизация [10]

Помимо КМИ к QUBO-решателям также относятся коммерческие квантовые компьютеры компании D-Wave Systems, основанные на квантовом отжиге. Данные вычислители используют в компаниях Volkswagen AG, Accenture, Lockheed Martin и в ряде других. Также многие крупные консалтинговые фирмы, такие, как BCG, предоставляют отчеты, дорожные карты и инвестиционные планы для области квантовых вычислений [11].

Исходя из приведенного выше, можно сказать, что использование квантовых вычислений на настоящий момент является не только технологических преимуществом, но и стремительно развивающейся областью мирового значения.

Рис. 3. Принципиальная схема КМИ. Фазочувствительный усилитель (PSA) усиливает 0- или π-фазовые компоненты входящего света в 5-километровом оптоволоконном кольцевом резонаторе. Включая и выключая PSA с временным интервалом 200 пс, мы генерируем ~ 120 000 импульсов DOPO. Часть энергии импульса разделяется светоделителем для измерения фаз и амплитуд. Для получения сигнала обратной связи для каждого импульса DOPO результаты измерений вводятся в схему быстрого умножения матриц, в которой заранее установлена заданная модельная задача Изинга (матрица 100 512 х 100 512). Сигнал обратной связи используется для модуляции оптического импульса, длина волны которого совпадает с длиной волны импульсов DOPO, и импульс вводится в соответствующий импульс DOPO, циркулирующий в резонаторе [4].

Литература:

1. Feynman R. P. Simulating Physics With Computers By R P Feynman.pdf // Int. J. Theor. Phys. 1982. Т. 21, № 6–7.
2. Aaronson S. BQP and the Polynomial Hierarchy // Proceedings of the Forty-Second ACM Symposium on Theory of Computing. New York, NY, USA: Association for Computing Machinery, 2010. С. 141–150.
3. Johnson M. W. и др. Quantum annealing with manufactured spins // Nature. 2011. Т. 473, № 7346.
4. Toshimori Honjo, Tomohiro Sonobe, Kensuke Inaba, Takahiro Inagaki, Takuya Ikuta, Yasuhiro Yamada, Takushi Kazama, Koji Enbutsu, Takeshi Umeki, Ryoichi Kasahara, Ken-ichi Kawarabayashi, Hiroki Takesue, "100,000-spin coherent Ising machine», Science Advances 7 (40), eabh0952 (2021).
5. Adamatzky A., Prokopenko M. Slime mould evaluation of Australian motorways // Int. J. Parallel, Emergent Distrib. Syst. Taylor & Francis, 2012. Т. 27, № 4. С. 275–295.
6. White paper. Optimization of Modern Data Centers using Fujitsu’s Quantum-Inspired Solutiontle. — Текст: электронный // Magdeburg Research and Competence Cluster: [сайт]. — URL: https://www.mrcc.ovgu.de/fileadmin/media/documents/fujitsu_lab/wp-da-dc-optimization-en.pdf (дата обращения 01.11.2022).
7. Venturelli D., Marchand D. J. J., Rojo G. Quantum Annealing Implementation of Job-Shop Scheduling. arXiv, 2015.
8. Weinberg, Sean & Sanches, Fabio & Ide, Takanori & Kamiya, Kazumitzu & Correll, Randall. (2022). Supply Chain Logistics with Quantum and Classical Annealing Algorithms.
9. R. Hamerly, T. Inagaki, P. L. McMahon, D. Venturelli, A. Marandi, T. Onodera, E. Ng, C. Langrock, K. Inaba, T. Honjo, et al. Experimental investigation of perfor-mance differences between coherent Ising machines and a quantum annealer Sci. Adv., 5 (2019), p. eaau0823
10. Mugel S. и др. Dynamic portfolio optimization with real datasets using quantum processors and quantum-inspired tensor networks // Phys. Rev. Res. APS, 2022. Т. 4, № 1. С. 13006.
11. The Next Decade in Quantum Computing — and How to Play. — Текст: электронный / P. Gerbert, F. Ruess // Strategic Management Consulting: [сайт]. — 2018. — URL: https://www.bcg.com/publications/2018/next-decade-quantum-computing-how-play (дата обращения 01.11.2022).