В работе представлены математические выкладки по определению параметров плотности распределения вероятностей мгновенных значений отраженного от неоднородной земной поверхности радиосигнала. Используется среда автоматизации математических вычислений MathCad. Приводятся структуры устройств оценивания, основанные на полученных формальных выражениях.
Ключевые слова : статистически неоднородная земная поверхность, радиосигнал, оценка параметров, MathCad.
The paper presents mathematical calculations for determining the parameters of the probability density distribution of the instantaneous values of the radio signal reflected from the inhomogeneous earth's surface. The automation environment for mathematical calculations MathCad is used. Structures of estimators based on the obtained formal expressions are given.
Keywords : statistically inhomogeneous earth's surface, radio signal, parameter estimation, MathCad.
При анализе точностных характеристик радиотехнических устройств, использующих сигнал, рассеянный статистически неоднородной поверхностью, необходимо знать законы распределения отраженного сигнала, а также основные статистические параметры этих законов распределения.
Для анализа закона распределения сигнала, отраженного от неровной поверхности (пашни), был проведен ряд наблюдений и измерений с последующей статистической обработкой результатов [1]. Экспериментально было показано, что плотности распределения вероятностей мгновенных значений отраженного сигнала, полученного при вертикальном облучении земной поверхности радиоволнами с длиной волны λ = 34 см, имеют характер распределения близкий к нормальному (рис. 1). При этом наблюдаются незначительные отличия в форме графических зависимостей при разных фазовых сдвигах между излучаемым и принимаемым сигналами, определяемых высотой над уровнем земной поверхности.
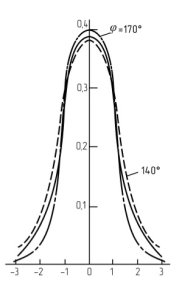
Рис. 1. Экспериментальная характеристика плотности распределения вероятностей сигнала, отраженного от неоднородной земной поверхности
Таким образом, фактически требуется оценить дисперсию и среднеквадратическую ширину спектра нормального действительного случайного процесса u с нулевым средним значением. Для получения совместных оценок воспользуемся теорией аналитического сигнала, определив для начала процесс v , сопряженный по Гильберту с процессом u .
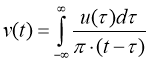
Тем самым мы определим обе компоненты (действительную и мнимую) аналитического сигнала s(t) = u(t) + j∙v(t).
Определим также понятия первой производной от обеих компонент аналитического сигнала du и dv соответственно. Тогда четырехмерная плотность распределения вероятностей нормального случайного процесса с нулевым средним будет иметь вид [2]:
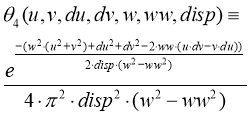
где disp — дисперсия действительного процесса, w — среднеквадратическая ширина спектра, ww — средняя частота спектра, определяемая длиной волны зондирующего радиосигнала.
Если считать последний параметр известным, то задача оценивания сводится, при отсутствии априорных данных о величинах
disp
и
w
, к поиску аналитических выражений для неизвестных дисперсии и среднеквадратической полосы. Для осуществления поиска этих выражений воспользуемся методом наибольшего правдоподобия. Для этого прологарифмируем функцию правдоподобия
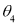
После упрощения в среде компьютерной математики [4] логарифм функции правдоподобия L примет вид, приведенный на рис. 2.
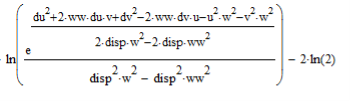
Рис. 2. Логарифм функции правдоподобия, вычисленный в среде MathCad
Вычислим в среде MathCad первую производную выражения по параметру disp, приравняем её к нулю (что соответствуем максимуму функции правдоподобия) и разрешим относительно дисперсии. Получим рис 3.
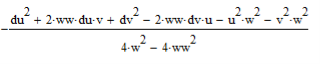
Рис. 3. Формальное выражение для дисперсии через среднеквадратическую ширину спектра, рассчитанное в среде MathCad
Подставим полученное выражение в формулу для функции правдоподобия, получив тем самым зависимость только от среднеквадратической ширины спектра. Результат после упрощения показан на рис. 4.
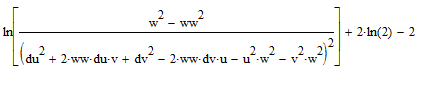
Рис. 4. Промежуточное выражение для логарифма функции правдоподобия после подстановки выражения для дисперсии, вычисленное в среде MathCad
Продифференцируем полученное выражение по искусственно введенной переменной w2 = w 2 , приравняем результат к нулю и разрешим относительно новой переменной. Получим оценку (рис. 5), зависящую только от полностью известных параметров.
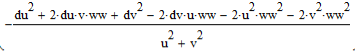
Рис. 5. Совместная оценка для среднеквадратической ширины спектра, полученная в среде MathCad
Подставим полученную оценку в выражение для дисперсии, определенное нами ранее. Заметим, что формальная оценка для дисперсии существенно упростится и окажется зависящей только от квадратов компонент исходного аналитического сигнала (рис. 6).
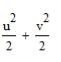
Рис. 6. Совместная оценка для дисперсии
Таким образом, структура устройства для оценивания дисперсии может быть представлена в следующем виде (рис. 7).
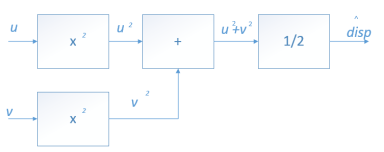
Рис. 7. Схематический вид структуры устройства для оценивания дисперсии сигнала, рассеянного над неоднородной земной поверхностью
Аналогичным образом можно представить и чуть более сложную структуру для оценивания среднеквадратической ширины спектра (рис. 8).
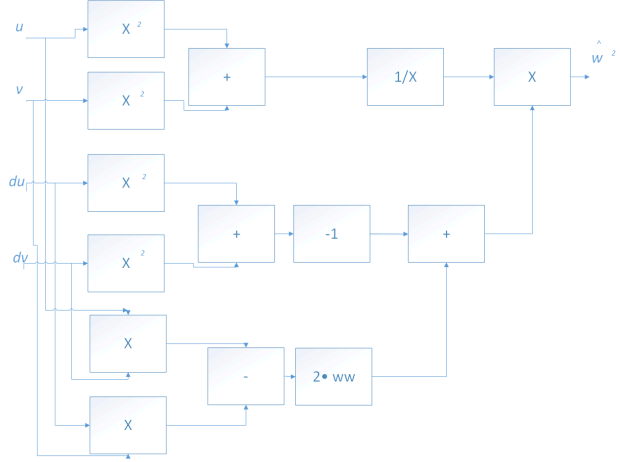
Рис. 8. Схематический вид структуры устройства для оценивания среднеквадратической ширины спектра сигнала
Вывод
Использование математического аппарата теории комплексного сигнала позволяет получить аналитические выражения для оценок параметров распределения сигнала, отраженного от неоднородной земной поверхности. Полученные формальные выражения определяют структуру устройств оценивания параметров, тем самым решается одна из важных задач прикладной радиотехники.
Литература:
- Жуковский А. П., Оноприенко Е. И., Чижов В. И. Теоретические основы радиовысотометрии. М.: Советское радио, 1979. 320 с.
- Фалеев С. П. Расчет и моделирование устройств обработки сигналов систем управления: учеб. пособие / Ленингр. электротехн. ин-т. Л., 1980. 110 с.
- Виноградова Е. П., Шепета А. П., Фалеев С. П. Автоматизация анализа и синтеза оценок параметров комплексной модели сигнала. СПб.: ГУАП, 2002.
- Кирьянов, Д. В. Mathcad 15/Mathcad Prime 1.0 / Д. В. Кирьянов. СПб.: БХВ-Петербург, 2012. 432 с.

