Разработка и оптимизация программного пакета для определения подлинности подписи в почерковедческой экспертизе



В данной работе рассматривается разработка программного обеспечения для перспективного метода идентификации подписи, основанного на изучении ее фрактальной размерности.

Ключевые слова: идентификация подписи, фрактальная размерность Минковского, box-counting алгоритм.

This paper discusses the development of software for a promising method of signature identification based on the study of its fractal dimension.

Keywords: signature identification, Minkowski fractal dimension, box-counting algorithm.

Судебное почерковедение является одним из видов криминалистической идентификации личности. Его суть состоит в сравнительном исследовании признаков письма, отобразившихся в документе, исполнитель которого неизвестен или вызывает сомнения, и признаков письма, имеющихся в образцах, написанных лицами, подозреваемыми в исполнении этого документа.

Под почерком в криминалистике понимается индивидуальная и динамически устойчивая программа графической техники письма, в основе которой лежит зрительно-двигательный образ выполнения рукописи, реализуемая с помощью системы движений. Следует отметить, что такие существенные свойства почерка, как индивидуальность и устойчивость, являются предметом изучения только криминалистики.

Подпись можно определить как собственноручно выполненное полное или частичное графическое изображение фамилии, имени, отчества конкретного лица или условное графическое начертание в виде письменных знаков, не образующих букв, нанесенное на документ в удостоверительных целях [1].

Изучение почерка и методы идентификации подписи основываются на методике, разработанной еще в СССР. В данной методике, являющейся основой для отечественного почерковедения, имеется фактор субъективности. Обработка подписи и оценка ее подлинности выполняется экспертом-почерковедом, который самостоятельно исходя из своего понимания теории общих и частных признаков исследования почерка, изучает конкретную почерковую реализацию и делает выводы [1].

Необходимо использование методов, способных увеличить объективность исследования почерка.

В данной работе рассматривается разработка программного обеспечения для перспективного метода идентификации подписи, основанного на изучении ее фрактальной размерности [2]. Используя его совместно с классической методикой исследования подписи, можно добиться повышения достоверности результатов за счет привлечения объективного, основанного на физических данных, способа [1].

Задача по автономному определению подлинности подписи широко изучается на сегодняшний момент, в связи с развитием технологий и увеличением количества использования электронных подписей, например, при осуществлении банковских переводов. Экспериментальные результаты новых методов, предложенных за последние несколько лет, показывают, что показатели успеха для английских подписей и китайских подписей составляют 91,71 % и 93 % соответственно [3].

В предложенном методе, основанном на математическом аппарате, описанным в работе [1], рассматривается траектория кончика пера пишущего прибора, которая подчиняется математическим уравнениям, благодаря которым, путем применения box-counting алгоритма для траектории пера, можно вычислить фрактальную размерность Минковского.

Любая надпись или подпись, оставленная человеком, может рассматриваться как годограф вектора (траектория движения конца вектора) положения ручки, который приводится в действие апериодической силой чьей-либо руки. Можно рассматривать такую траекторию как движение точки на плоскости. Если внешняя сила случайна, то это движение можно описать двумя дифференциальными уравнениями второго порядка в четырехмерном фазовом пространстве координат и скоростей. Эти уравнения также являются нелинейными, поэтому поиск решения для них, как для замкнутых траекторий без каких-либо дополнительных параметров, представляет почти неразрешимую задачу.

Однако существуют методы решения данной проблемы. Одним из таких методов является использование фракталов. Это геометрические объекты с дробной размерностью пространства Минковского, тогда как обычные кривые имеют целочисленную размерность Минковского. Этот параметр определяет тип поведения в различных хаотических моделях нелинейной динамики, финансовых рынках и прочих [3].

С целью автоматизации описанного алгоритма и возможности автоматизированного набора статистки был предложен программный код, написанный с использованием языка программирования Python и библиотек, предназначенных для распознавания графических элементов изображений.

Отсканированная и распознанная при помощи программного кода подпись приведена на рис. 1. Видно, что полученное изображение имеет различную плотность цвета, что соответствует различному нажиму и плотности чернил в исследуемой подписи. В перспективе это может быть использовано для анализа степени нажатия пера, что несет в себе дополнительную информацию о подписи.

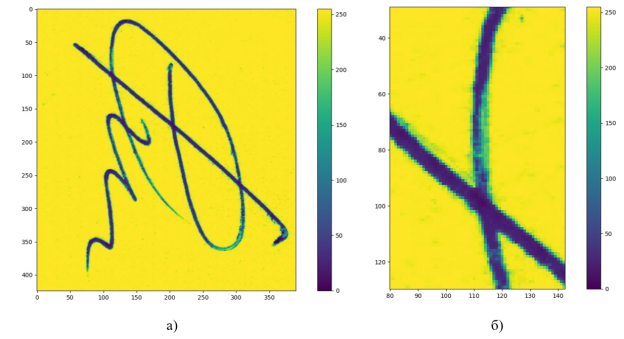
Рис. 1. а) — Пример автоматизированного получения разрабатываемой программой изображения подписи из скана; б) — увеличенный участок полученного программой изображения для анализа степени нажатия пера

После получения программой изображения необходимо получить его поточечное разбиение (сечение Пуанкаре), с целью применения box-counting алгоритма для вычисления фрактальной размерности Минковского. Пример разбиения подписи на точки путем использования программного кода приведен на рис. 2.

После получения сечения Пуанкаре необходимо вычислить размерность Минковского. Рассмотрим подробнее box-counting алгоритм:

Объект покрывается квадратной сеткой с ячейками известного размера

Подсчитывается количество ячеек, которые оказались содержащими фрагмент исследуемого объекта. Сохраняется пара значений «размер (длина стороны) ячейки»(ε) — «количество ячеек, содержащих объект»(N).

Сетка детализируется — т. е. размер ячеек уменьшается, и, соответственно, количество ячеек, содержащих объект, увеличивается. Сохраняется новая пара значений.

Процедура детализации повторяется многократно.

Согласно методу вычисления размерности Минковского, её значение будет равно угловому коэффициенту линии регрессии, построенной на плоскости по рядам значений log(N) и log(1/ ε).

Таким образом сравнивая значения размерности Минковского для оригинальной и фальсифицированной подписи, мы можем определить поддельную [2].

В данной работе был обработан один набор из 64 оригинальных подписей и три набора фальсифицированной подписи (7, 8 и 32 шт.), выполненные различными людьми. Количество разбиений в box-counting алгоритме варьировалось от 4 до 48. Результаты вычисления фрактальной размерности для оригинальной подписи приведены на рис. 3.

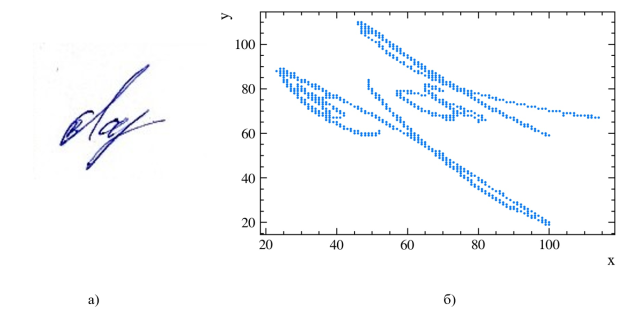
Рис. 2. а) — Пример выполнения подписи; б) — разбиение подписи на точки программным образом

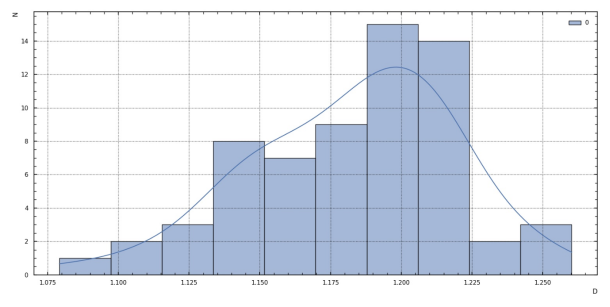
Рис. 3. Распределение значения фрактальной размерности D для оригинальной подписи в зависимости от числа отсчетов

Параметры аппроксимации Гауссом для полученных значений фрактальной размерности оригинальной подписи: µ = 1,182; σ2 = 0,001.

На рис. 4. приведено сравнение вычисленных значений фрактальной размерности для оригинальных и фальсифицированных подписей. Количество подписей в соответствии с номерами на рис. 4: «1» — 7 шт., «2» — 8 шт., «3» — 32 шт. Значения аппроксимации Гауссом для полученных данных приведены в табл. 1.

Таблица 1

Результаты аппроксимации функцией Гаусса полученных данных для фальсифицированных подписей

Номер в легенде	Количество подписей, шт.	µ	σ 2
1	7	1.348	0.00022
2	8	1.36	0.00047
3	32	1.3	0.00031

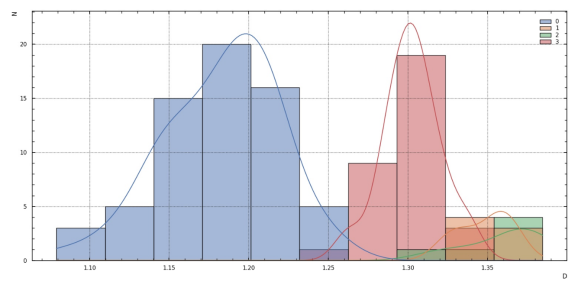
Рис. 4. Значения размерности Минковского для оригинального набора подписей и для трех наборов фальсифицированных подписей

Также для наглядности были построены линии регрессии (рис. 5) для полученных данных. Верхняя группа линий принадлежит оригинальным подписям, нижняя принадлежит фальсифицированным подписям. Из полученных наборов данных видно, что средние значения размерности Минковского сильно отличаются для оригинальной и фальсифицированной подписей. Таким образом подтверждается теоретическая возможность использования данного метода, в качестве дополнительного критерия при определении подлинности подписи.

В настоящий момент для полного подтверждения объективности данного критерия, авторы ставят перед собой задачу о расширении базы различных подписей и увеличения статистических данных. Также в настоящий момент рассматривается вопрос о возможности применения данного метода не только к подписям, но и частям рукописного текста, с целью увеличения областей применимости данного подхода в почерковедческой экспертизе.

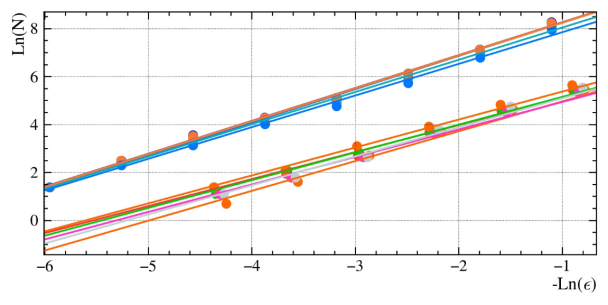
Рис. 5. Линии регрессии для оригинальных подписей (сверху) и фальсифицированных (снизу)

Литература:

1. Матюхов, А. А. Перспективный метод идентификации подписи в почерковедческой экспертизе / А. А. Матюхов, А. Ю. Рождественский // Неделя науки СПбПУ: Материалы науч. конф. с междунар. уч. — Санкт-Петербург: ФГАОУ ВО «Санкт-Петербургский политехнический университет Петра Великого», 2020. — С. 79–81. — EDN OHPXIY.
2. Rudyi, S. S. Signature identification by Minkowski dimension / S. S. Rudy, T. A. Vovk, Y. V. Rozhdestvensky // Chaos: An Interdisciplinary Journal of Nonlinear Science. — 2019. — V. 29. — No. 5. — 053110. — DOI: 10.1063/1.5092270.
3. Deng, P. S. Wavelet-based offline handwritten signature verification / P. S. Deng, H.-Y. M. Liao, C. W. Ho, H. R. Tyan // Computer vision and image understanding. — 1999. — V. 76. — No 3. — Pp.173–190.