В статье рассматривается вопрос применения фрактальной размерности Минковского (метод Box-Counting Dimension) для определения использованного в тексте шрифта на основе результата цифрового копирования или фотографического изображения. Анализируются популярные методы классификации шрифтов. Приводятся результаты предварительного эксперимента по применению фрактальной размерности для анализа отдельного слова.
Ключевые слова: распознавание шрифта, фрактальная размерность Минковского, Box-Counting Dimension.
The article discusses the issue of using the Minkowski fractal dimension (Box-Counting Dimension method) to determine the font used in the text based on the scan result or photographic image. Popular methods of font classification are analyzed. The results of a preliminary experiment on the use of fractal dimension for the analysis of a single word are presented.
Keywords: font recognition, Minkowski fractal dimension, Box-Counting Dimension.
Вопрос определения семейства шрифтов текста на электронных копиях документов или их фотографиях, не считается первоочередным, но стоит рассмотреть области его применения. Одним из возможных применений можно считать задачу определения подлинности документов. Так в [1] описывается возможность применения смартфонов и сверточных нейронных сетей для проверки подлинности паспорта гражданина РФ на основе номера. Данный подход может использоваться только для отсечения при проверке документов, которые были созданы с использованием неверного шрифта.
Другим, более распространенным, применением является предварительный анализ документа для распознавания на нем текста. Определение использованных шрифтов позволяет минимизировать ошибки и сократить уровень зашумленности результатов распознавания. Такой подход применяется в некоторых средства просмотра электронных копий документов.
Подчеркну, что на сегодняшний день не существует единого или наиболее оптимального универсального подхода. Так, одни авторы [2, 3] предлагают применения метода, основанного на анализе отклонения контура анализируемых символов от эталона. В то время как другие [4] определяют ряд классификаторов: наклон, засечки, морфологические моменты (дисковое r-покрытие фигуры, r-площадь фигуры, морфологическая ширина фигуры). И, наконец, третьи [5, 6] — используют различные нейронные сети для выявления неявных признаков и классификации на их основе (машинное обучение).
В данной статье, в качестве основного метода предлагается использовать фрактальную размерность Минковского. Этот подход может применяться в различных областях, например при определении подлинности подписи [7, 8]. Созданная для описания стохастических систем, фрактальная размерность позволяет выделить детерминированные факторы, исключая случайные [7]. Стоит отметить кардинальное отличие машинописных шрифтов и подписи человека — закон, которому подчиняются элементы шрифта (символы) заранее известен, но самих шрифтов (кроме, конечно, популярных) существует слишком много. Кроме этого, у шрифтов кроме классического или обычного написания присутствуют такие как полужирное, наклонное и другие; текст может быть набран с разной размерностью (кеглем).
Идея этой статьи основывается на гипотезе, что на основе фрактальной размерности Минковского текста или его фрагмента возможно определение использованных шрифтов, их начертания и размерности. Каждый символ шрифта воспринимается как набор метрик, а слова и тексте как функции от этих метрик, которые можно проанализировать с применением фрактальной размерности. Проверка такой гипотезы — достаточно длительный процесс и с точки зрения сбора материала, и с точки зрения проведения самих экспериментов. Рациональность такого исследования можно определить подтверждением упрощенной гипотезы: фрактальная размерность отдельного слова, фразы или предложения, выполненных разными шрифтами с одинаковыми характеристиками будет достаточно сильно отличаться.
Для подтверждения этой гипотезы было взято одно из самых длинных слов русского языка, в котором нет повторяющихся букв [9]: предоставляющий. В слове присутствует 15 букв (почти половина алфавита), слово было воспроизведено десятью популярными и общедоступными шрифтами (половина из которых с засечками) на областях 100 на 600 пикселей с разрешением 300dpi популярным размером 14пт. Примеры написания приведены на рис. 1.

Рис. 1. Исходные данные для эксперимента
Фрактальная размерность Минковского, вычисляемая обычно по формуле:
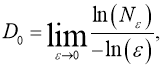
где D 0 — фрактальная размерность, N ε — минимальное число множеств диаметра ε , была заменена алгоритмом Box-Counting Dimension, определяющим на каждой итерации, в какое количество клеток N ε размером ε попадает значимая часть изображения (в данном случае — контур символа). В таком случае искомое значение фрактальной размерности — D — для выбранного ключевого слова будет угловым коэффициентом уравнения линейной регрессии. Для анализа были взяты все возможные целые значения от 100 (минимальная сторона исходного изображения) до 1. Промежуточные результаты для шрифтов без засечек и с засечками приведены на рис. 2 и 3 (соответственно). Горизонтальная ось содержит значения размерности ячейки ( -ln(ε) ), вертикальная — количественный показатель ( ln(N ε ) ).
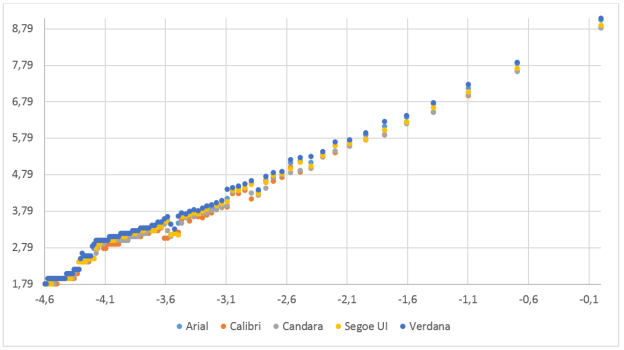
Рис. 2. Зависимость количества точек от размерности ячейки для шрифтов без засечек
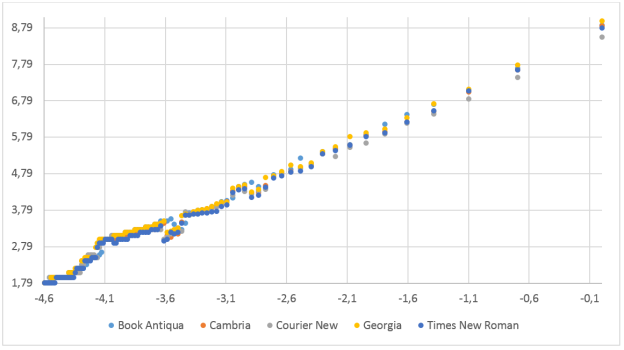
Рис. 3. Зависимость количества точек от размерности ячейки для шрифтов с засечками
Из рис. 2 и 3 видно, что при некоторых размерах ячейки происходит сокращения числа занятых исследуемым изображением точек, однако, в общем, их число растет. Далее на рис. 4–13 приводится детальный анализ для каждого шрифта, результат приводится в таблице 1.
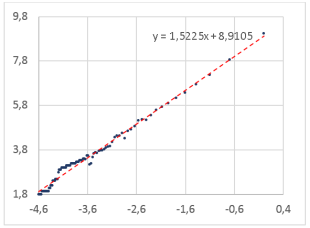
Рис. 4. Определение фрактальной размерности слова для шрифта Arial
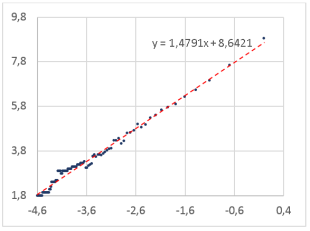
Рис. 5. Определение фрактальной размерности слова для шрифта Calibri
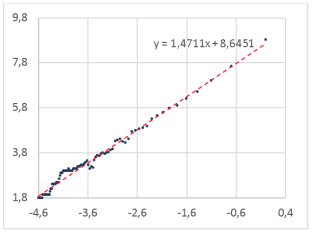
Рис. 6. Определение фрактальной размерности слова для шрифта Candara
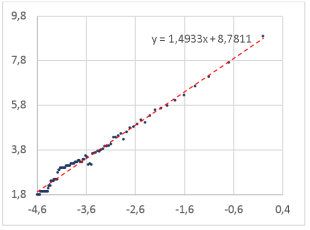
Рис. 7. Определение фрактальной размерности слова для шрифта Segoe UI
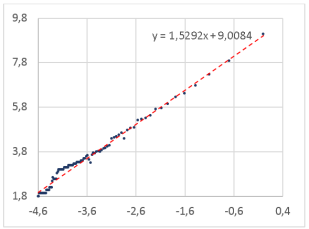
Рис. 8. Определение фрактальной размерности слова для шрифта Verdana
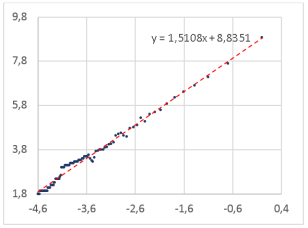
Рис. 9. Определение фрактальной размерности слова для шрифта Book Antiqua
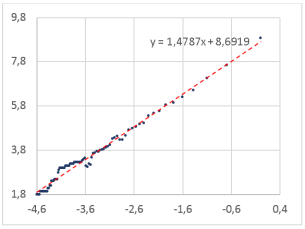
Рис. 10. Определение фрактальной размерности слова для шрифта Cambria
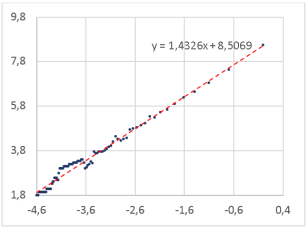
Рис. 11. Определение фрактальной размерности слова для шрифта Courier New
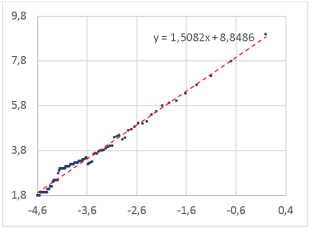
Рис. 12. Определение фрактальной размерности слова для шрифта Georgia
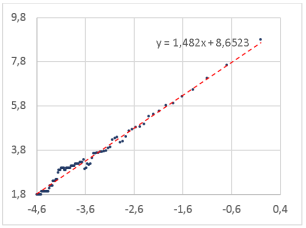
Рис. 13. Определение фрактальной размерности слова для шрифта Times New Roman
Таблица 1
Фрактальная размерность слова «Предоставляющий»
|
№ п/п |
Шрифт |
Фрактальная размерность Минковского |
|
1 |
Arial |
1,5225 |
|
2 |
Calibri |
1,4791 |
|
3 |
Candara |
1,4711 |
|
4 |
Segoe UI |
1,4933 |
|
5 |
Verdana |
1,5292 |
|
6 |
Book Antiqua |
1,5108 |
|
7 |
Cambria |
1,4787 |
|
8 |
Courier New |
1,4326 |
|
9 |
Georgia |
1,5082 |
|
10 |
Times New Roman |
1,4820 |
Полученные в результате исследования результаты (таблица 1) позволяют сделать вывод, что при точности четыре знака после запятой (точность четырехбайтного вещественного числа в памяти компьютера — 7 знаков) фрактальная размерность выбранного слова, воспроизведенного разными шрифтами, достаточно отличается, чтобы можно было идентифицировать используемый шрифт. Следовательно, можно проводить эксперименты с целью выявления способов идентификации шрифтов в результатах цифрового копирования с применением фрактальной размерности Минковского.
Литература:
- Чернышова, Ю. С. Оптическое распознавание шрифтов на изображениях, полученных со смартфонов, и его использование для определения подлинности документов, удостоверяющих личность / Ю. С. Чернышова, М. А. Алиев, А. В. Шешкус // Труды Института системного анализа Российской академии наук. — 2018. — Т. 68. — № S1. — С. 183–191. — DOI 10.14357/20790279180521. — EDN VMVCCU.
- Коробов, Д. В. Метод распознавания шрифта текста с изображения / Д. В. Коробов, М. В. Патин // Молодой ученый. — 2016. — № 12(116). — С. 161–165. — EDN WGFNPN.
- Belongie, S. Shape Matching and Object Recognition Using Shape Contexts / S. Belongie, J. Malik, J. Puzicha // IEEE Transactions on Pattern Analysis and Machine Intelligence. — 2002. — V. 24. — No. 4. — Pp. 509–522. — DOI: 10.1109/34.993558.
- Липкина, А. Л. Распознавание шрифтов по изображениям на основе анализа структуры букв / А. Л. Липкина, Н. А. Ломов, Л. М. Местецкий // GraphiCon 2017: Труды 27-й Междун. конф. по комп. граф. и маш. зрен. / ПГНИУ. — Пермь: Издательский центр ПГНИУ, 2017. — С. 359–366. — EDN USOFFM.
- Tensmeyer, C. Convolutional Neural Networks for Font Classification / C. tensmeyer, D. Saunders, T. Martinez // 2017 14th IAPR International Conference on Document Analysis and Recognition (ICDAR), 2017. — Pp. 985–990. — DOI: 10.1109/ICDAR.2017.164.
- A Multi-Implicit Neural Representation for Fonts / P. Reddy, Z. Zhang, M. Fisher [et al.] // Advances in Neural Information Processing Systems 34 (NeurIPS 2021). — Curran Associates, Inc., 2021. — Pp. 12637–12647.
- Софина, Д. Как фрактальная размерность Минковского помогает определить подлинность подписи человека. — Текст: электронный // Новости Университета ИТМО: [сайт]. — 2019. — URL: https://news.itmo.ru/ru/news/8529/ (дата обращения: 01.11.2022).
- Rudyi, S. S. Signature identification by Minkowski dimension / S. S. Rudy, T. A. Vovk, Y. V. Rozhdestvensky // Chaos: An Interdisciplinary Journal of Nonlinear Science. — 2019. — V. 29. — No. 5. — 053110. — DOI: 10.1063/1.5092270.
- Интересные слова русского языка. — Текст: электронный // Орфограммка: [сайт]. — URL: https://orfogrammka.ru/интересная_филология/интересные_слова_русского_языка/ (дата обращения: 01.11.2022).

