- Понятие геометрической информации
- Всякий моделируемый объект обладает вполне определенной пространственной формой, имеет заданные метрические характеристики и занимает некоторое положение в соответствующем пространстве
.
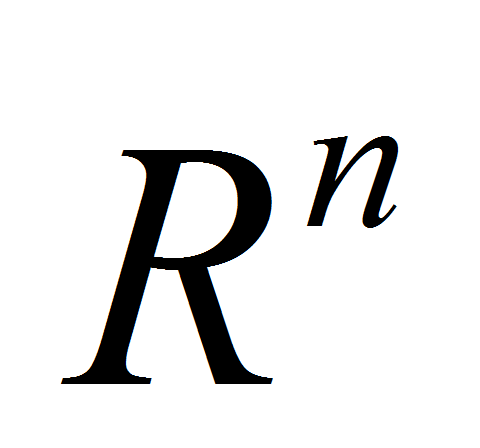Указанные характеристики задают так называемую геометрическую
информацию об объекте. В понятие геометрической информации
включается [1]: - Всякий моделируемый объект обладает вполне определенной пространственной формой, имеет заданные метрические характеристики и занимает некоторое положение в соответствующем пространстве
-
совокупность пространственных форм
; -
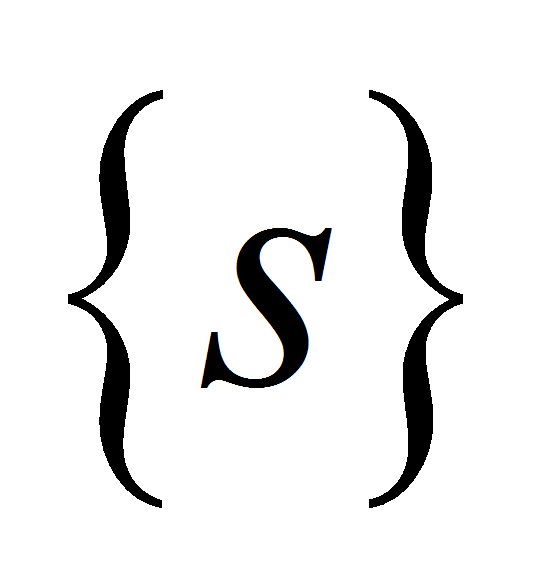метрические характеристики
,
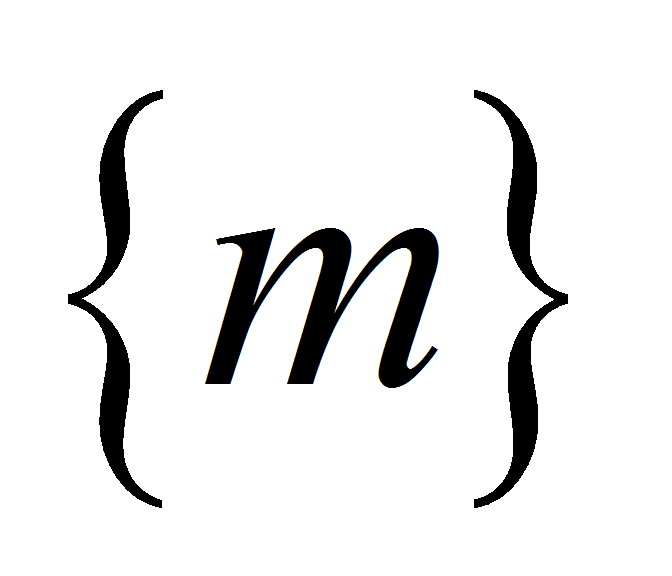определяющие «размеры» точечных множеств, имеющих формы
из
; -
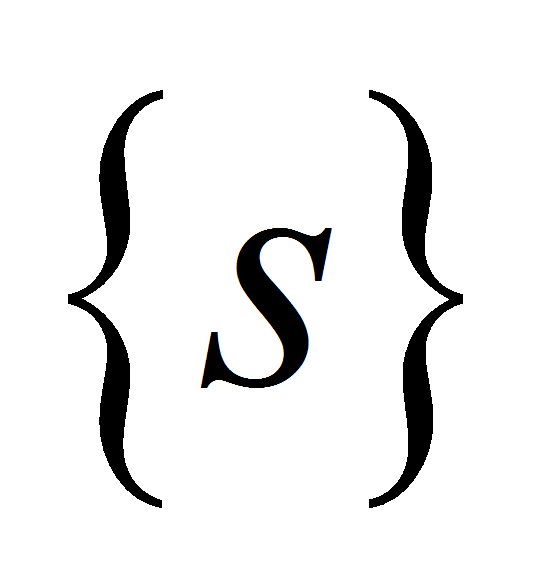параметры
,
задающие местоположение точечных множеств в соответствующих
пространствах.
- Соответственно геометрическая информация представляется в виде
набора
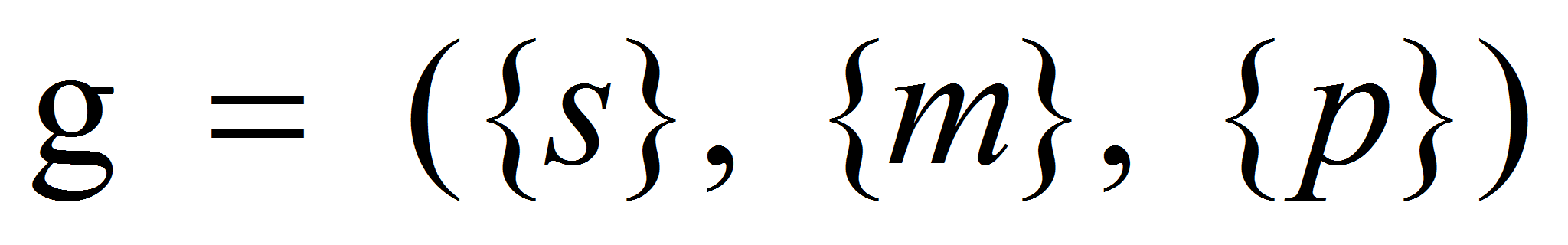.- Например, метрической характеристикой точечного множества
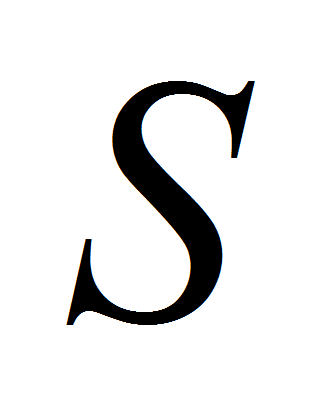в пространстве
,
имеющего форму квадрата, является длина
стороны этого квадрата, а его положение на плоскости определяется
тремя параметрами: координатами
,
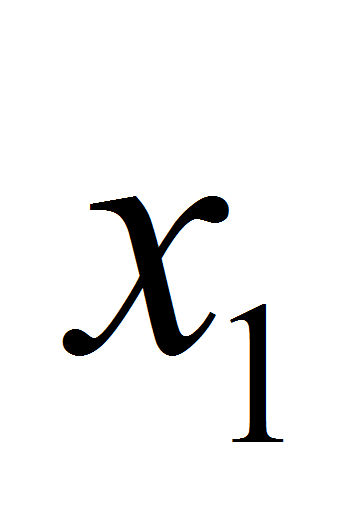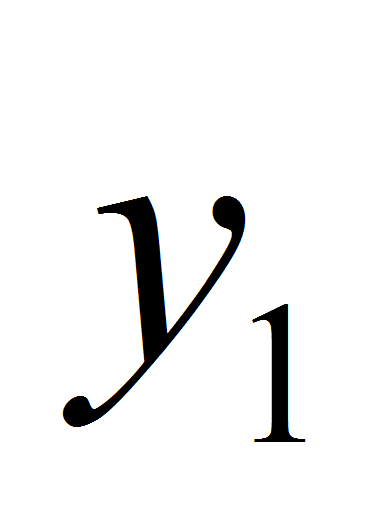полюса
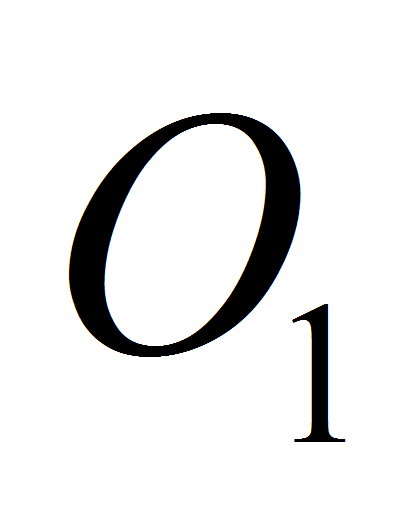и углом
между осью абсцисс собственной системы координат
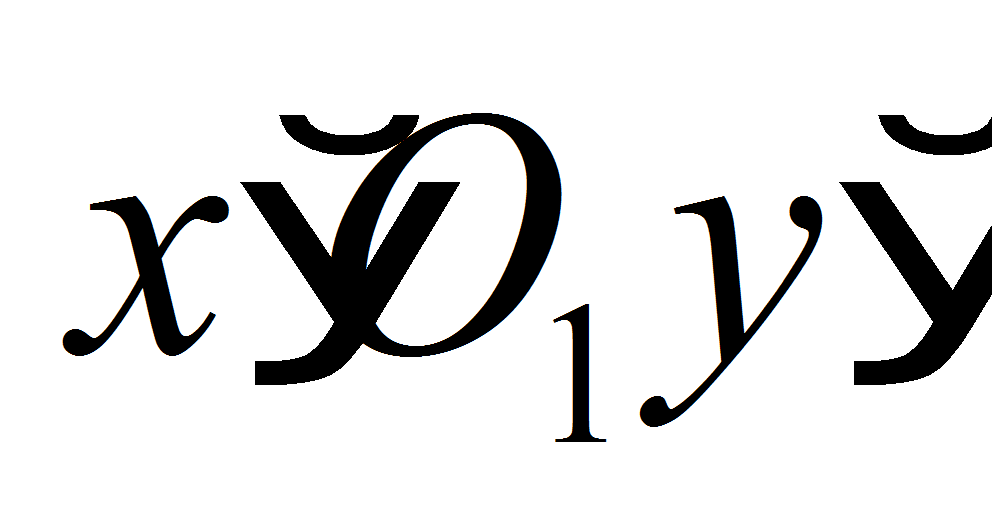и осью абсцисс системы координат
.
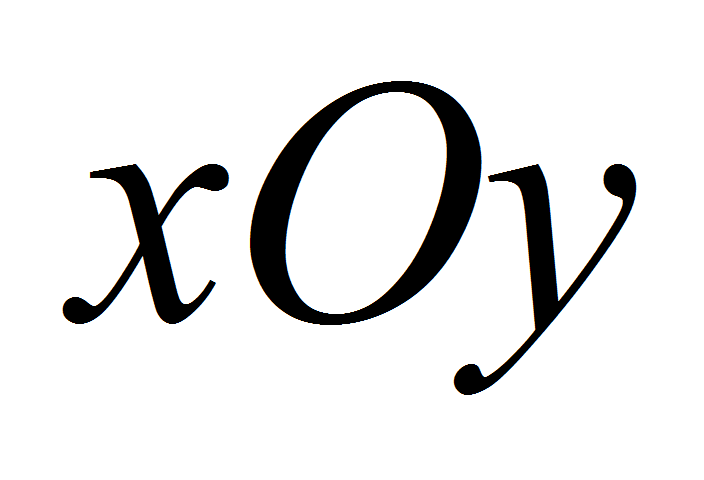В этом случае информация, индуцирующая точечное множество
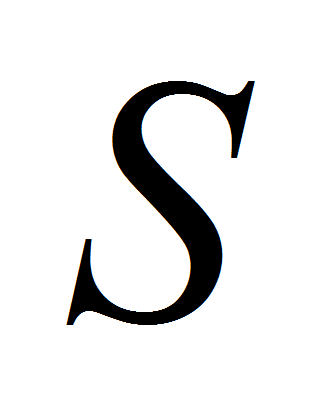примет вид
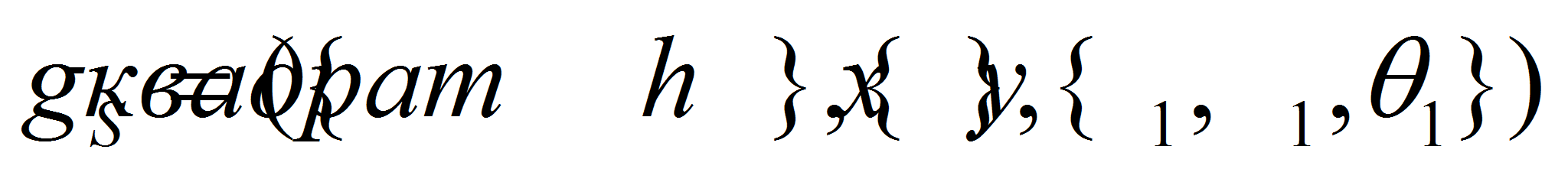.- Отметим, что компонент
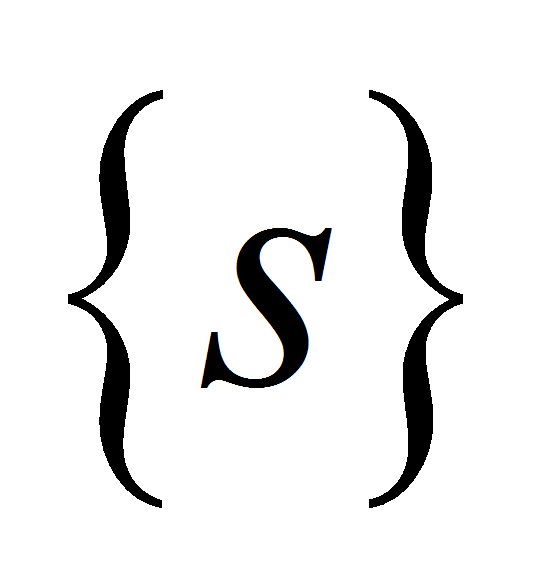геометрической информации всегда не пустой, в отличие от
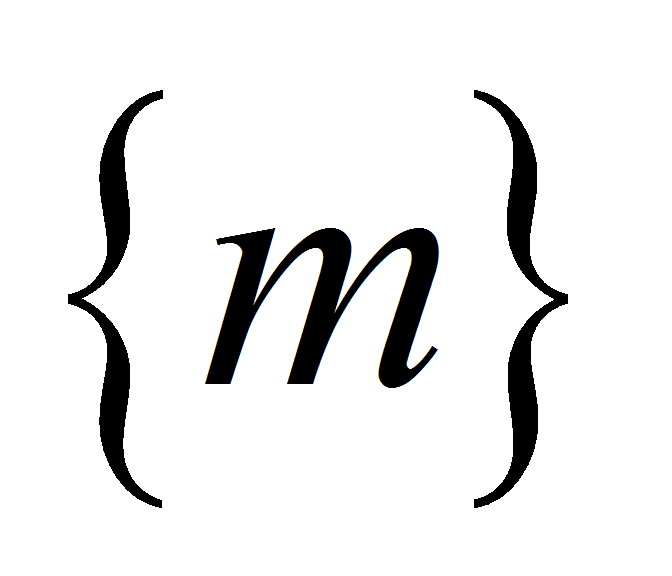и
.- Носителем формы объекта также является и граница этого объекта, которая, в свою очередь, может быть задана в любом удобном виде. Например, каноническое уравнение эллипсоида с полуосям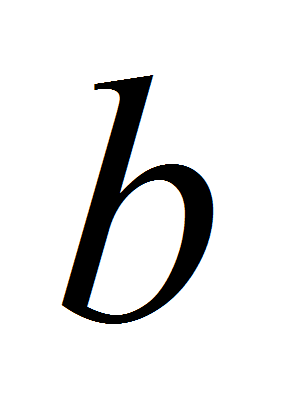и
,
и
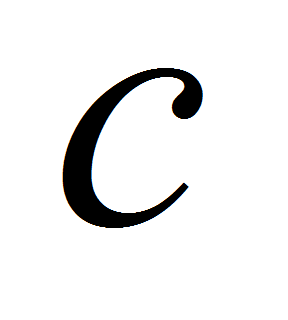имеет вид
,- где
,
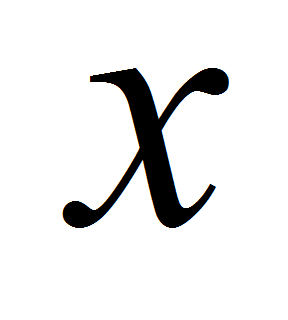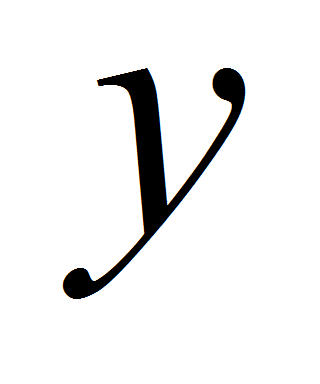и
–
точки границы объекта. Это уравнение одновременно носитель формы и
носитель метрических характеристик, а именно:
,
.
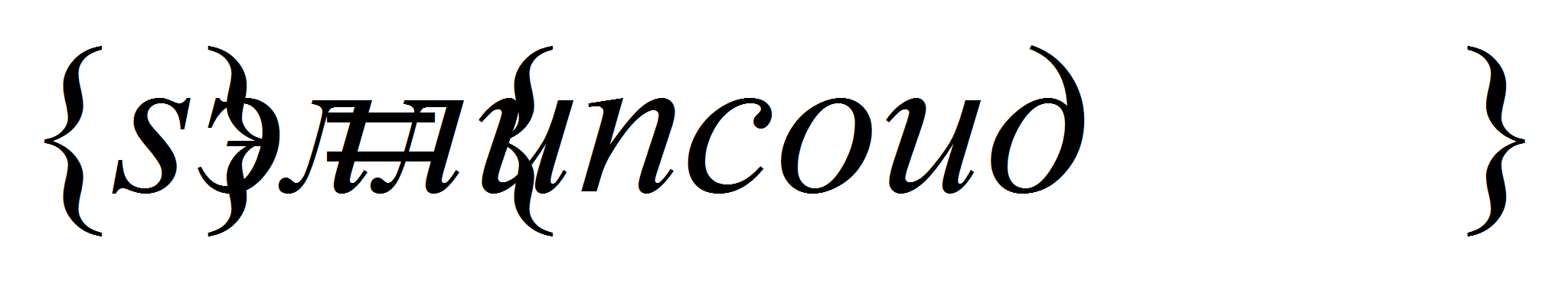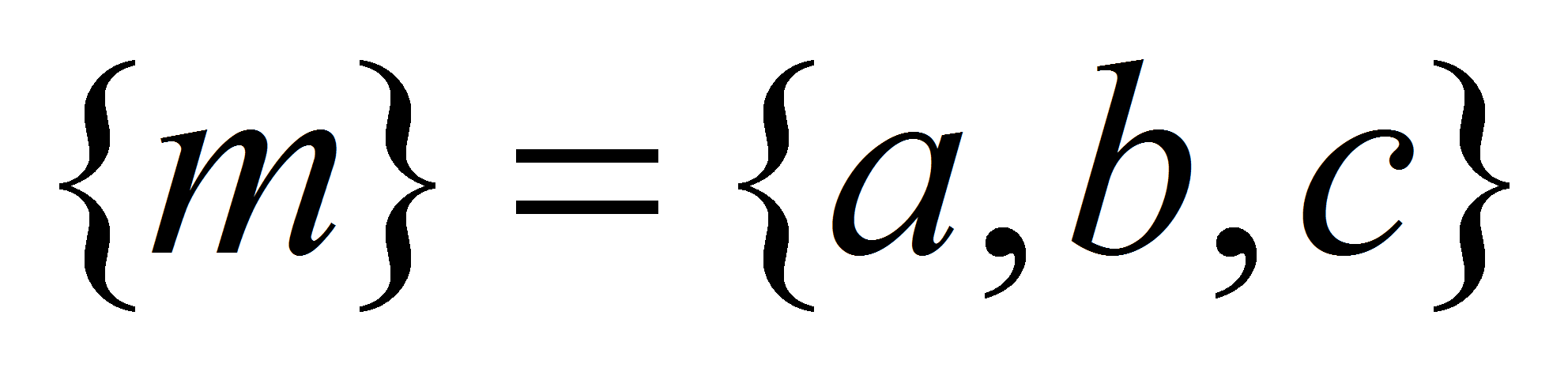Компонентом
можно пренебречь, если локальная система координат объекта совпадает
с системой координат пространства.- Если объект имеет сложную форму, например такую, как голова человека, компонент
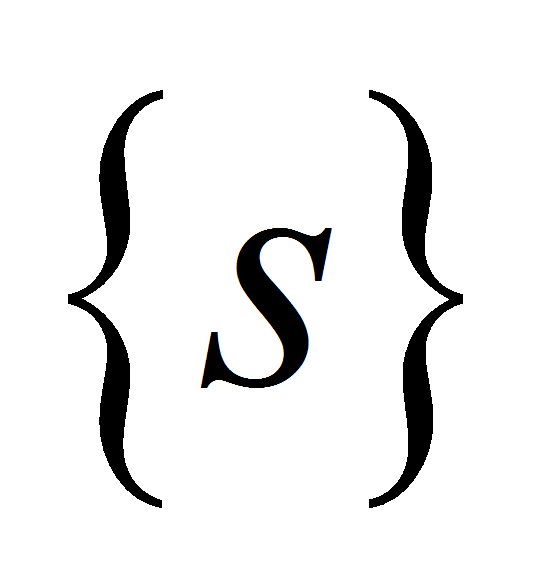не всегда возможно выразить в аналитическом или
параметрическом виде. В этом случае используют структурный подход,
выделяя две составляющие части: набор структурных элементов и
топологию (структуру, определяющую способ взаимосвязи элементов).- Под сжатием геометрической информации мы будем понимать способы наиболее компактного и удобного параметрического описания класса объектов, с возможностью создания в соответствии с этим описанием конкретного экземпляра класса [2].
- Способы представления трехмерного объекта
- В общем случае в любой геометрической модели, как уже было сказано, можно выделить две составляющие ее части: набор структурных элементов
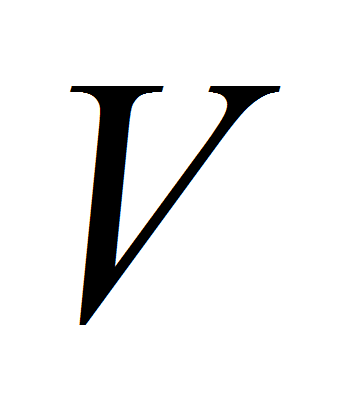и топологию
.
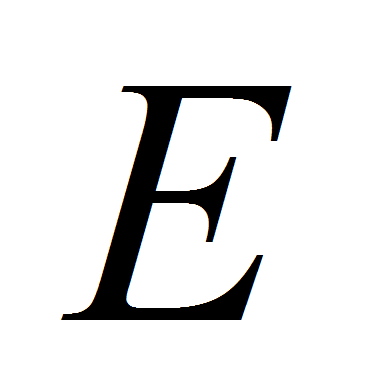Из структурных элементов конструируется различная топология,
выражающая отношения между структурными элементами. Например,
ломаную линию на плоскости можно представить совокупностью множества
вершин
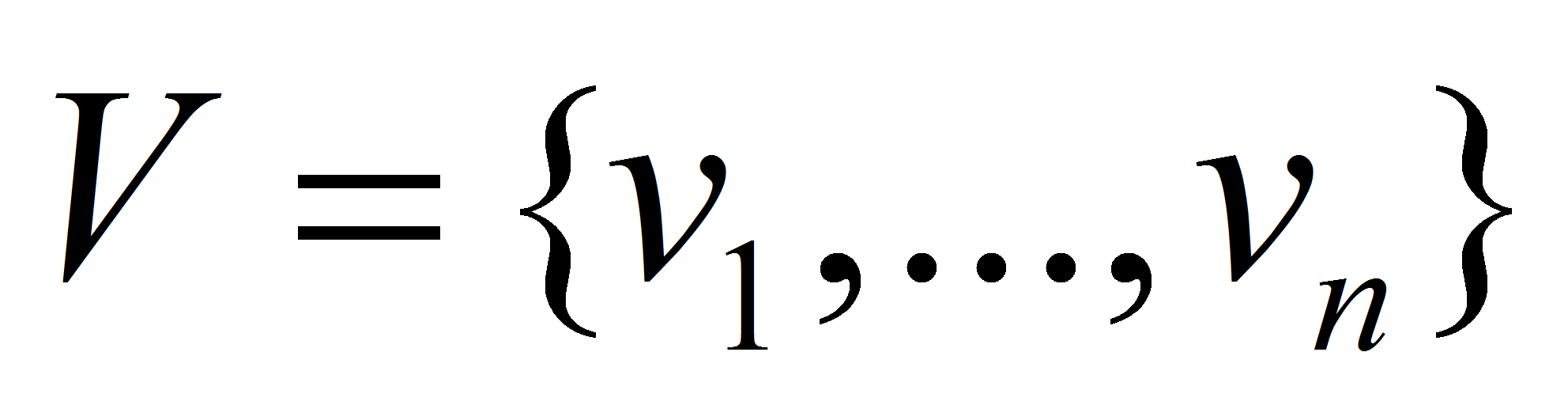и множества ребер
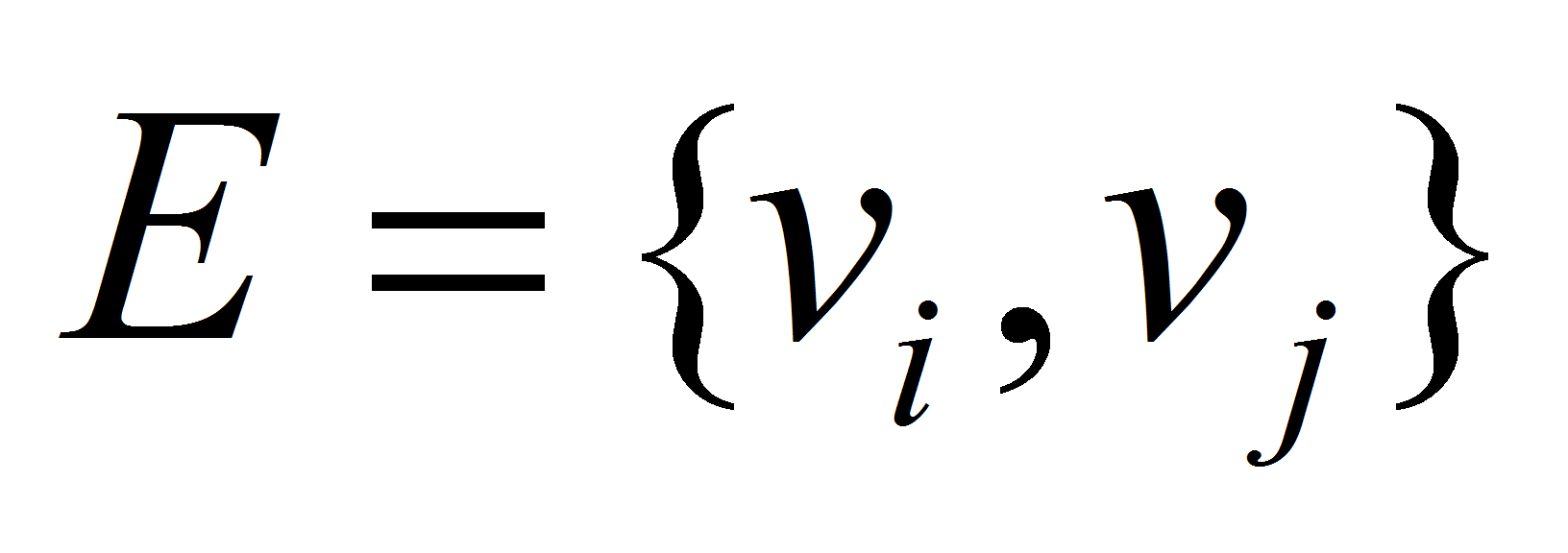.- В зависимости от выбранного структурного элемента выделяются основные способы представления трехмерных объектов:
- точечное;
- каркасное (проволочное);
- поверхностное (граничное);
- объемное.
- В точечном представлении объект задан совокупностью вершин,
принадлежащих поверхности объекта
.- Каркасная (проволочная) модель является расширением точечного способа. Объекты задаются совокупностью вершин
и соединяющих их ребер (отрезков прямой или кривой)
.
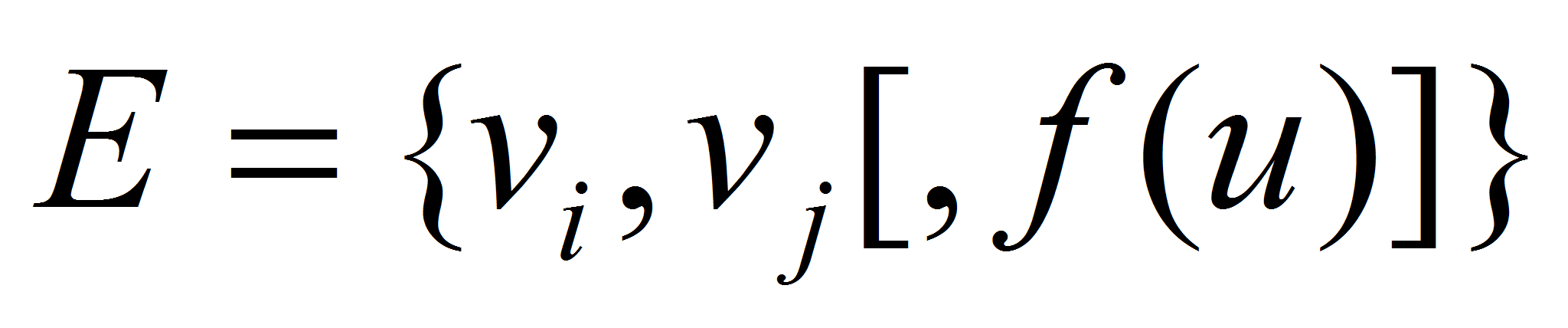Функция
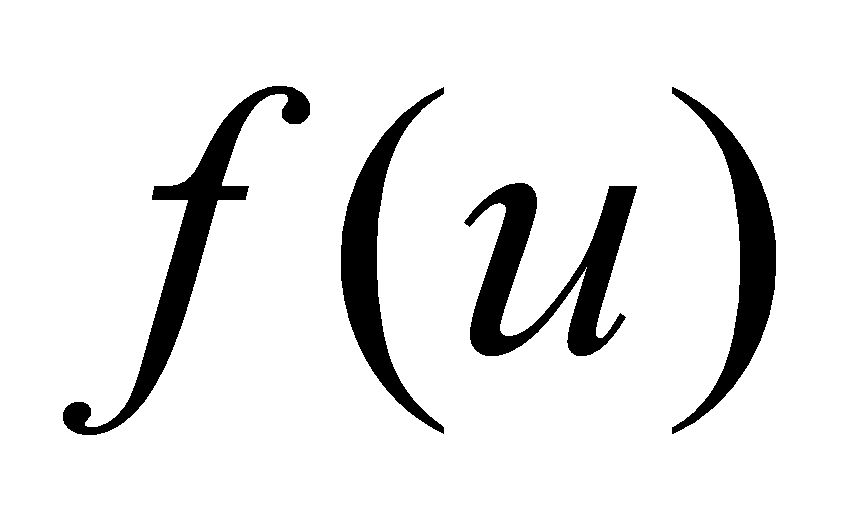определяет линию, соединяющую вершины
,
,
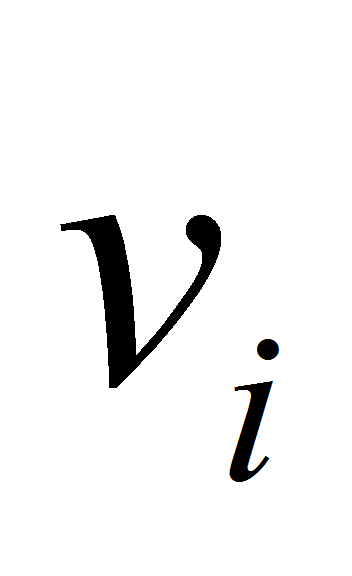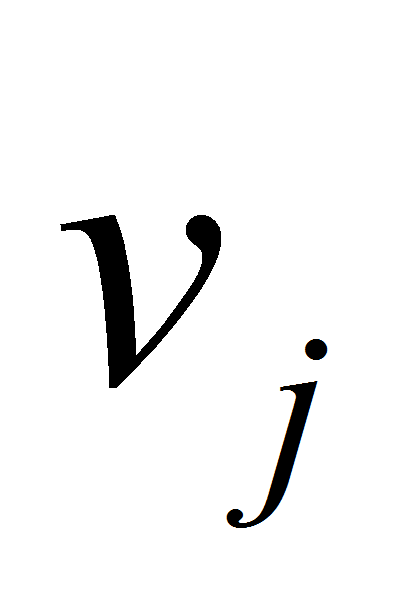когда ребро не является отрезком прямой. Как правило, для одной
модели эта функция является векторной функцией одного и того же
типа. Различают три вида каркасных поверхностей [3]: поверхности,
основанные на движении, поверхности натяжения, производные
поверхности.- Поверхности, основанные на движении, создаются путем перемещения каркасов в пространстве. Это поверхности вращения, сдвига и изгиба.
- Поверхности натяжения создаются путем обтягивания каркаса. После удаления каркаса поверхность сохраняет его форму. Различают следующие типы поверхностей натяжения: поверхности соединения, плоские усеченные поверхности и поверхности, натянутые на один или два набора линий каркаса. Поверхность соединения строится соединением двух линий каркасов любой трехмерной формы. Она может располагаться между любыми двумя непересекающимися каркасами, представляющими верх и низ. Каркасы могут быть как замкнутыми, так и разомкнутыми.
- Производные поверхности строятся на основе существующих поверхностей путем смещения исходных поверхностей, а также путем сопряжения поверхностей.
- При поверхностном (граничном) представлении объекта в качестве структурного элемента выступает поверхность, она описывается явно параметрическим способом или в виде неявных функций.
- Параметрически заданной (в локальном смысле) поверхностью обычно называют множество
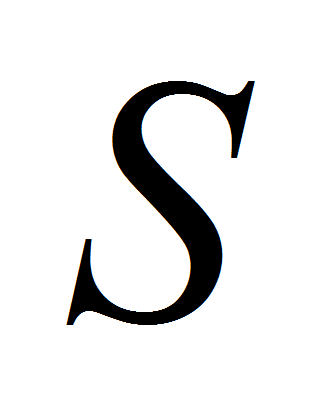точек
пространства, декартовы координаты
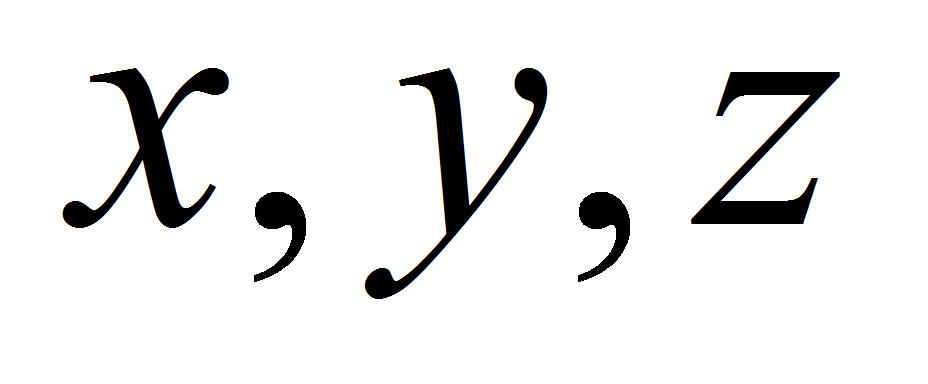которых определяются по средствам соотношений: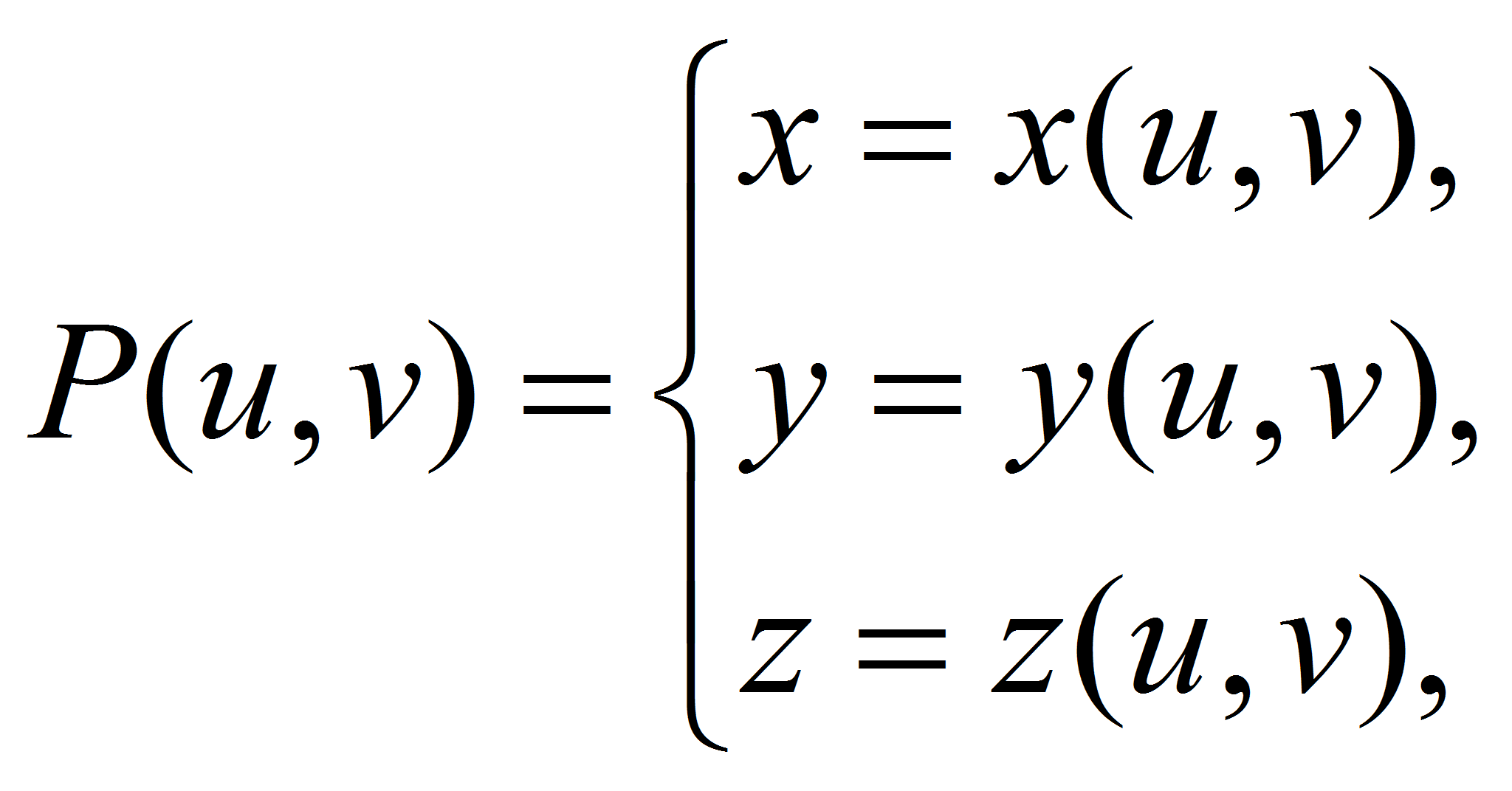
- где
,
,
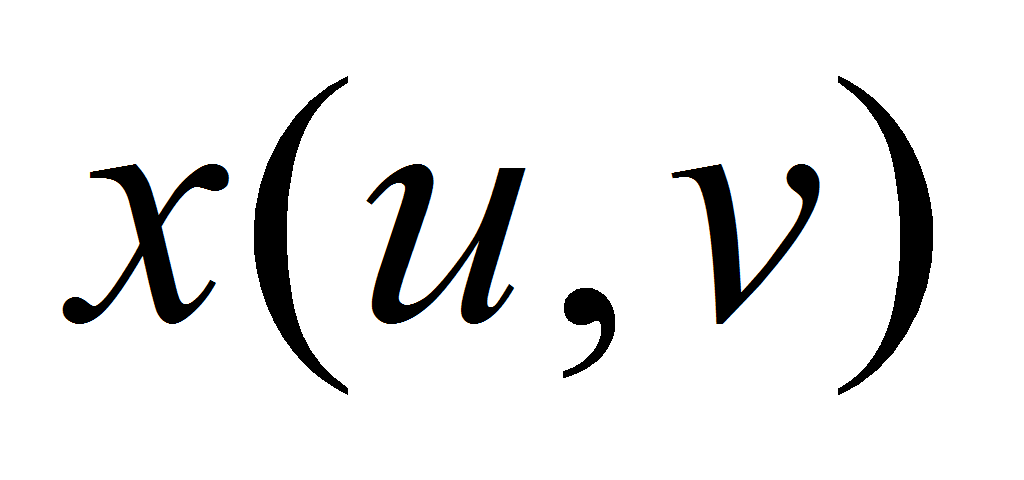– функции, непрерывные в прямоугольнике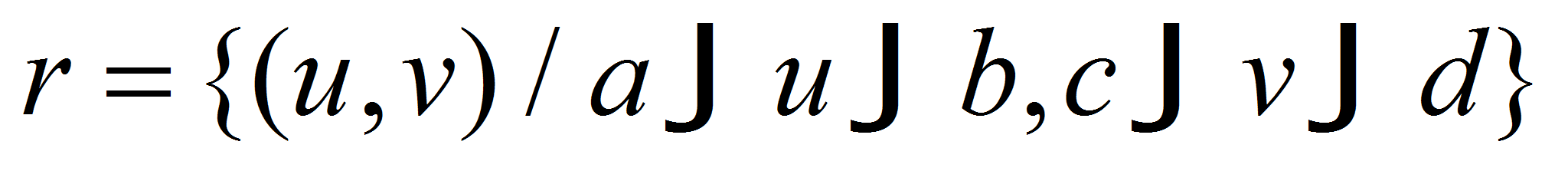
- или треугольнике
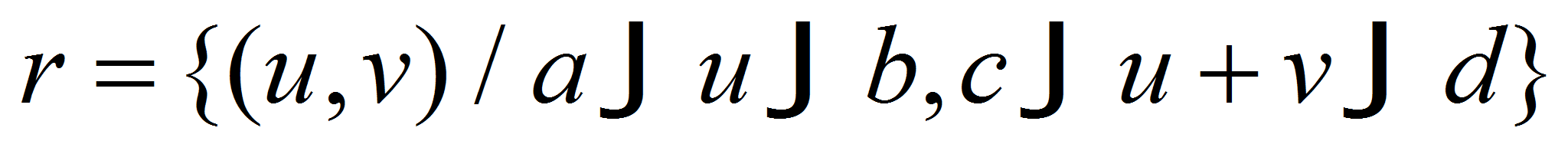.- Величины
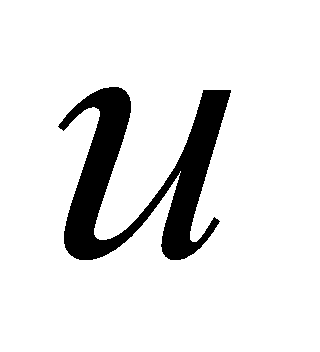и
,
называются внутренними криволинейными координатами на поверхности
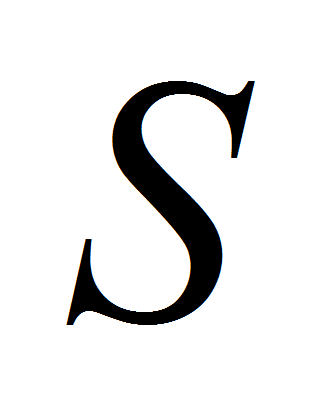.- Выделяются два основных типа поверхностных параметрических моделей: полигональная модель, которая представлена набором плоских граней; патч-модель, или лоскутная модель, где гранями служат части поверхностей одного типа (например, билинейные, поверхности Кунса, бикубические поверхности, поверхности Безье, поверхности на основе B-сплайнов и др.).
- В объемном представлении базовыми являются области в пространстве или неявно представленные примитивы. Наиболее известны воксели, метаболы, сплошные конструктивы.
- Основой воксельного представления служит воксель (или ячейка), представляющий собой кубическую область пространства. Трехмерный объект определяется как массив вокселей.
- Метаболы – это шары различного радиуса
,
которые могут взаимодействовать в зависимости от близости и радиуса
взаимодействия
.
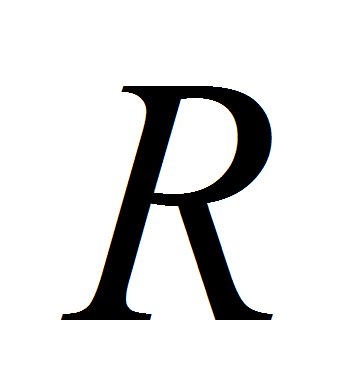Взаимодействие выражается через появление дополнительной «материи»
между ними. Топология как таковая в этом случае отсутствует.- При представлении объекта в виде сплошных конструктивов используется набор базовых примитивов (параллелепипед, сфера, конус, цилиндр, тор, призма, пирамида и т.п.), являющихся структурными элементами объекта, и набор теоретико-множественных операций: унарного аффинного преобразования и бинарных операций вычитания, пересечения, объединения. Данный набор определяет топологию модели, которая реализуется в виде формулы теории множеств.
- Сжатие геометрической информации сложного объекта
- Рассмотрим сложный материальный объект в трехмерном пространстве. В качестве объекта-прототипа используется женский манекен. Первичными данными об объекте может выступать точечная модель женского манекена, полученная путем трехмерного сканирования.
- Определим геометрическую информацию
,
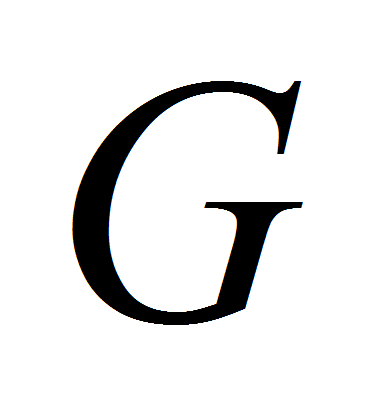индуцирующую точечное множество
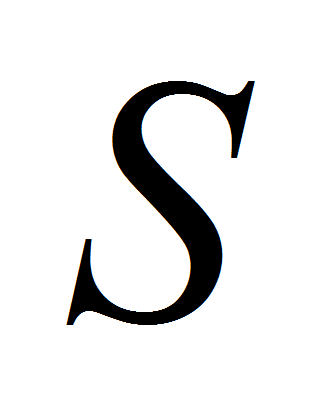в пространстве
,
имеющего форму женского манекена. Компонентом формы объекта
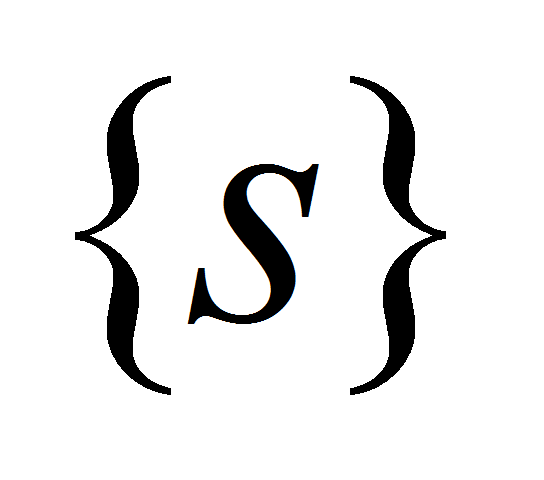выбрана геометрическая каркасная модель манекена с поверхностью
соединения в качестве типа математической модели поверхности.
Исходными данными для такой поверхности являются координаты
сканированных точек на заданных сечениях и представление
соответствующего сечения в виде сглаживающей эти точки кубической
B-сплайновой кривой. Точность
аппроксимации поверхностью соединения, натянутой на сплайны соседних
сечений, будет определяться количеством узлов разбиения сплайнов на
элементарные участки. Таким образом
,
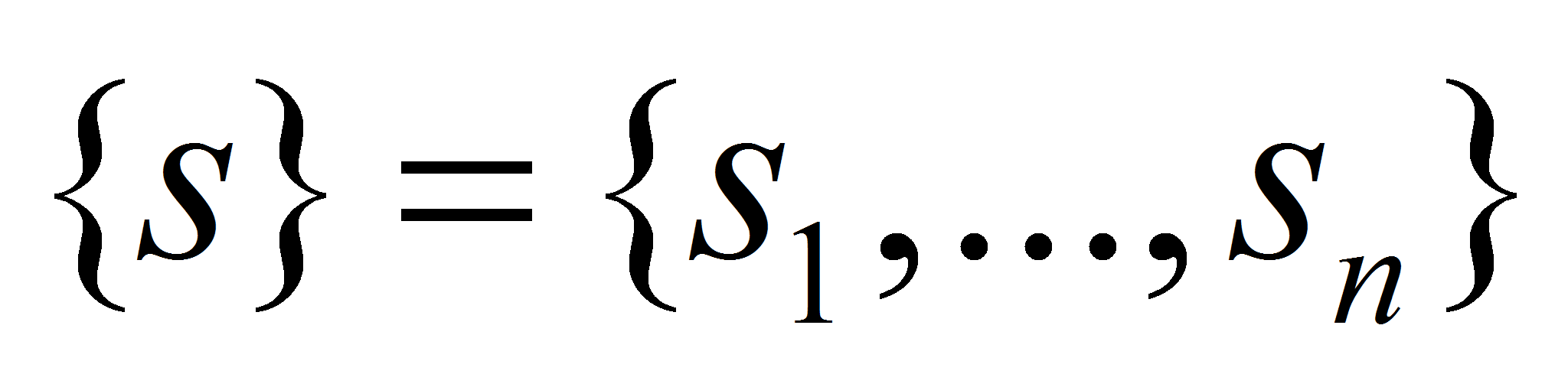где
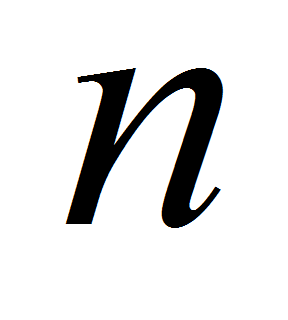– количество B-сплайн кривых
(сечений), описывающих форму объекта.- Для определения сечений используется государственный стандарт ГОСТ 17521-71 «Типовые фигуры женщин. Размерные признаки для проектирования одежды». В этом стандарте определены 17 антропометрических точек и 70 размерных признаков характеризующих женскую фигуру. Возможны различные варианты определения множества сечений. Рассмотрим, например, вариант расположения горизонтальных сечений на уровне следующих антропометрических точек [4]:
- Каркасная (проволочная) модель является расширением точечного способа. Объекты задаются совокупностью вершин
- шейной;
- верхне-грудинной;
- плечевой;
- выступающей точки грудной железы;
- нижнего основания грудной железы;
- высоты талии;
- остисто-подвздошной точки;
- выступающей точки живота;
- выступающей точки бедер;
- подъягодичной складки;
- 1/3 бедра.
- Каждое сечение характеризуется набором размерных признаков
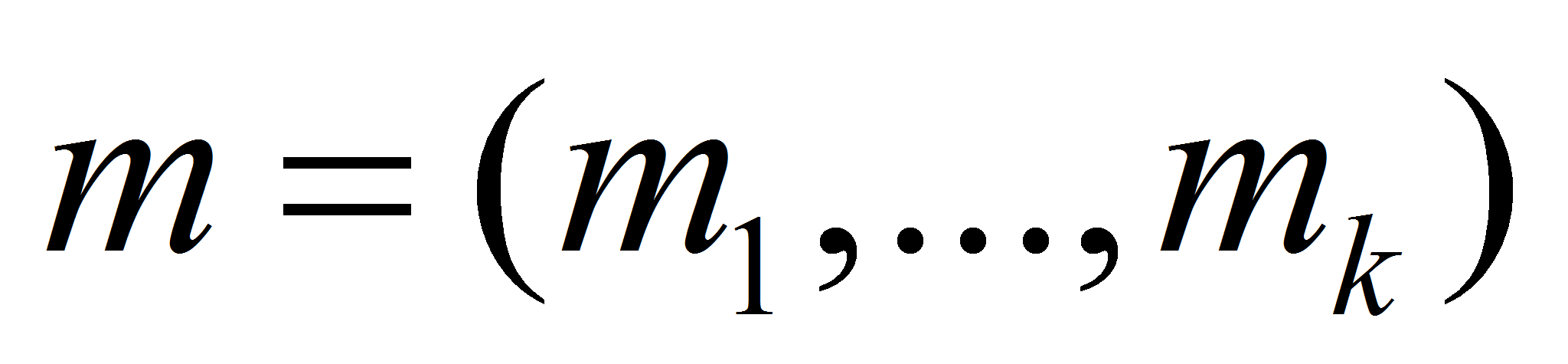– метрических характеристик B-сплайновой
кривой.
- Параметрами
,
задающими местоположение объекта в пространстве, являются:
координаты
,
,
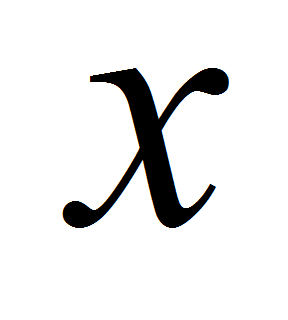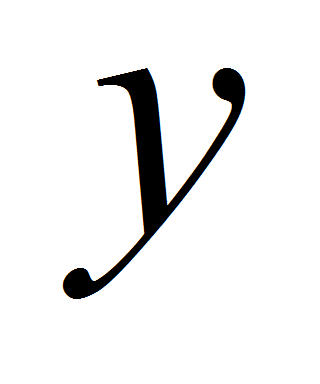точки пересечения вертикальной оси и плоскости опоры и углы
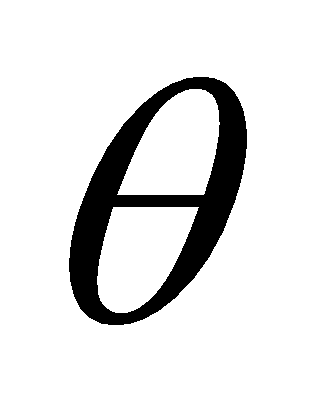и
между осью абсцисс и осью ординат собственной системы координат и
глобальной системы координат. Также для каждого сечения определяется
высота
уровня соответствующей антропометрической точки.- Таким образом, если положить, что вертикальная, поперечная и сагиттальная плоскости тела совпадают соответственно с осями аппликат, ординат и абсцисс глобальной системы координат, информация, описывающая i-ое сечение манекена примет вид:
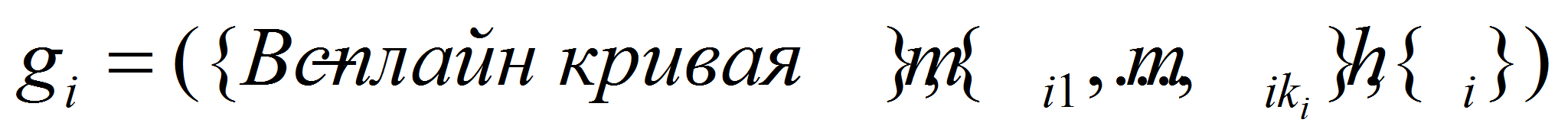,- где
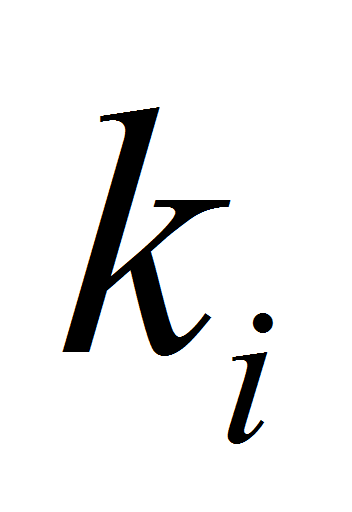– количество метрических характеристик i-го сечения. Тогда
геометрическая информация, определяющая точечное множество
выбранного материального объекта определяется следующим образом: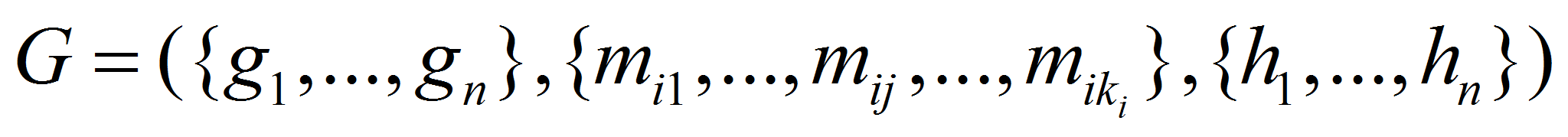
.- Определив геометрическую информацию сложного объекта конкретного класса, становиться возможным получить множество объектов того же класса, изменяя метрические характеристики. Этот принцип используется в системах параметрического моделирования, на вход которых подается базовая модель
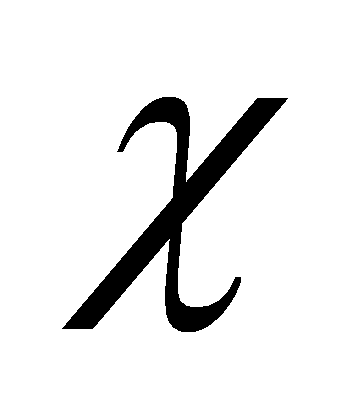и набор параметров
для ее изменения. Результатом является деформированная модель
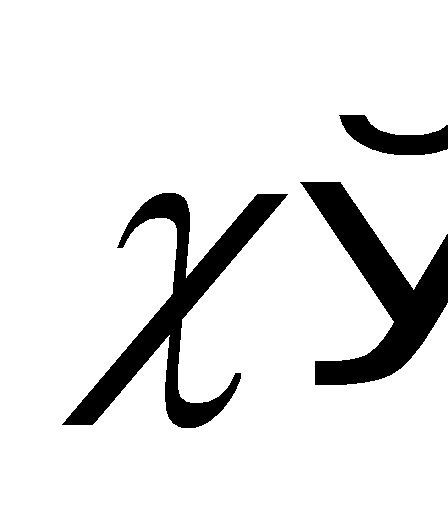соответствующая введенным параметрам.
- Литература:
- Параметрами
- Стоян Ю. Г. Математические модели и оптимизационные методы геометрического проектирования / Ю. Г. Стоян, С. В. Яковлев – Киев: Наук. думка, 1986. – 268 с.
- Балжирсурэн Г. Автоматизация проектирования нестандартных компьютерных манекенов: Дисс. канд. тех. наук. Новосибирск. 2009. – 157 с.
- Фроловский В. Д. Избранные задачи геометрического проектирования. Параметризация сложных поверхностей. Учебное пособие. Новосибирск. Изд-во НГТУ. 2005. – 165 с.
- Коблякова Е. Б. Размерная типология населения с основами анатомии и морфологии / Е. Б. Коблякова, Т. Н. Дунаевская, Г. С. Ивлева, Р. В. Иевлева; Под ред. Е. Б. Кобляковой: Учеб. пособие для студ. учреждений сред. проф. образования. – М.: Мастерство; Издательский центр «Академия», 2001. – 288 с.