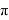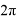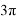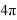Рассмотрим простую механическую задачу — у меня есть цилиндр и веревка, которую я наматываю на цилиндр. Между цилиндром и веревкой есть трение, и это трение удерживает веревку на цилиндре. Сделаем два витка и повесим легкий предмет
И видим — несколько граммов удерживают полкилограмма. Какая же связь между этими силами?


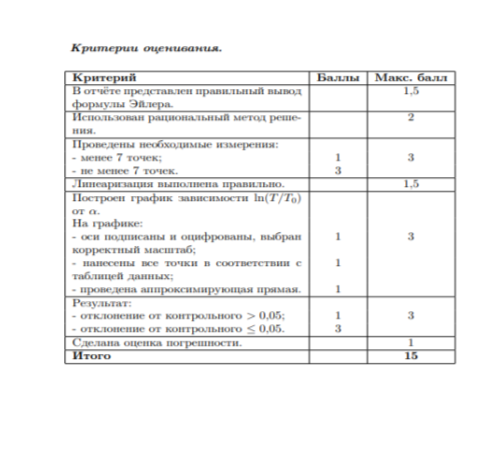
- Изучение трения нити о неподвижный цилиндр
Цель работы: исследование трения нити о поверхность неподвижного цилиндра и экспериментальная проверка формулы Эйлера.
Оборудование: легкая и прочная хлопчатобумажная нить, динамометр, набор грузов разной массы (разновесы), 3 стеклянных цилиндра различного диаметра, штатив.
Теоретическая часть
Достаточно часто в жизни и технике возникает трение гибких тел (веревок, нитей, тросов) о блоки, цилиндрические поверхности. Например, в подъемных механизмах, устройствах крепления. Данный вид трения учитывают в текстильной, рыболовной промышленности, используют альпинисты, закручивая в несколько оборотов страховочный трос о выступы скал. Мы используем этот вид трения, завязывая шнурки или узлы на веревке (при этом один шнурок служит осью для накручивания другого).
Многие наверняка видели, каким образом сдерживают ход судна, подошедшего к пристани. С палубы на пристань кидают конец каната с широкой петлей. Человек на пристани набрасывает ее на причальную тумбу, а кинувший канат матрос быстро укладывает второй его конец между палубными кнехтами — спаренными чугунными тумбами. Сила трения между кнехтами и канатом надежно стопорит судно. Как правило, матрос, намотав канат восьмеркой на кнехты несколько раз, просто наступает на свободный конец, прижимая его к палубе. Такого малейшего усилия вполне хватает для удержания громадного судна.
Впервые изучил трение веревки о цилиндр математик Леонард Эйлер и вывел формулу, позволяющую определить отношение сил натяжения веревки на «входе» и «выходе» с поверхности цилиндра.
Рассмотрим блок с перекинутой через него веревкой. Пусть к концам веревки приложены силы натяжения Т 1 и Т 2 , как показано на рис. 1. Методы описания движения тел, связанных идеальной нитью, в системах, содержащих неподвижные и подвижные блоки, подробно описаны в пособии [4]. Однако в этих системах трение между нитью и блоком настолько мало, что не оказывает существенного влияния на движение тел и не учитывается при решении задач. Найдем соотношения между силами Т 1 и Т 2 в случаях, когда нить можно полагать идеальной, но между поверхностью блока и нити существует сила трения.
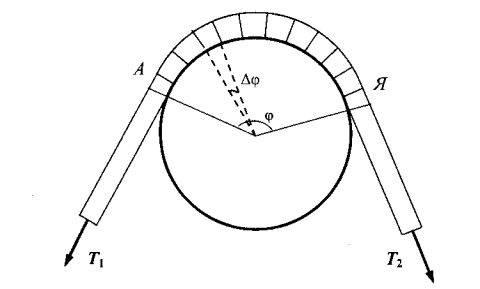
Рис. 1. Схема блока с перекинутой через него веревкой
Сначала выберем на нити сечения А и Я, которые ограничивают криволинейный участок нити, лежащий на блоке (см.рис.1). Разделим участок нити А-Я на маленькие элементы, которые далее будем рассматривать как материальные точки. Каждый элемент нити представляет собой дугу, опирающуюся на малый центральный угол Δφ.
На каждый элемент нити массы mi,- действуют 5 сил: силы натяжения Ti-1 и Ti+1 со стороны соседних элементов нити, сила тяжести mig и сила реакции Ni со стороны поверхности блока, сила трения Fтр i, где i — порядковый номер элемента. Сила реакции Ni перпендикулярна касательной к окружности блока в точке расположения данного элемента нити, сила трения направлена по касательной против направления скорости движения нити (см. рис. 2).
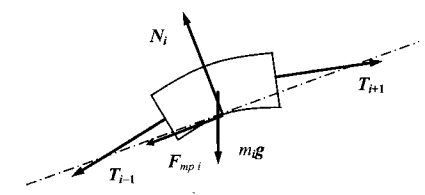
Рис. 2. Силы, действующие на i-й элемент нити.
Штрихпунктирная линия — касательная к окружности блока, проведенная через среднюю точку нижней дуги данного элемента нити.
Силы натяжения Ti-1 и Ti+1 действуют со стороны соседних элементов нити и направлены перпендикулярно сечениям, ограничивающим элемент нити. Сила нормальной реакции Ni действует со стороны поверхности блока и направлена перпендикулярно поверхности блока в месте нахождения данного элемента нити. Сила тяжести тig направлена вертикально вниз.
Все сечения, которые делят нить на элементы, проведены перпендикулярно нити. Соседние сечения, ограничивающие некоторый элемент нити, непараллельны относительно друг друга из-за кривизны нити, охватывающей блок. Силы натяжения Ti-1 и Ti+1 направлены перпендикулярно соответствующим сечениям и, следовательно, угол между ними отличается от 180° (см. рис. 2).
Заменим i-й элемент нити материальной точкой и приложим к ней все действующие на неё силы (см. рис. 3). Запишем уравнение движения для i- го элемента нити:
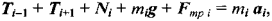
где а* — ускорение i-го элемента нити.
Элементы идеальной нити имеют пренебрежимо малые массы, что позволяет упростить уравнение движения:
(1.2)
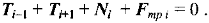
Направим координатную ось X вдоль касательной к блоку в точке расположения i-го элемента нити (см. рис. 3). Из симметрии элемента следует, что углы (Δφ/2) отклонения векторов сил Ti-1 и Ti+1 от оси X равны между собой (см. рис. 3).
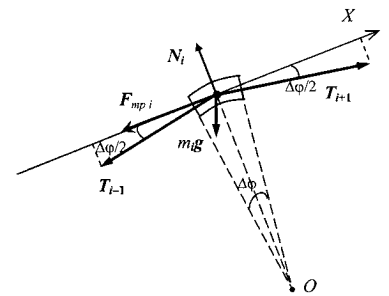
Рис. З. Элемент нити, превращенный в материальную точку.
Координатная ось X параллельна касательной к окружности блока в месте нахождения данного элемента нити. Точка О расположена на оси блока. Спроецируем на ось X уравнение движения (2):
Ti+1 cos(Δφ/2) — Ti-1 cos(Δφ/2) — Fтр i = 0(3)
Компоненты сил натяжения Ti-1 и Ti+1 перпендикулярные оси X, компенсируются нормальной силой реакции Ni.
Ti+1 cos(Δφ/2) + Ti-1 cos(Δφ/2) — N i = 0(4)
Мы разбивали нить на очень маленькие элементы, которые можно считать материальными точками, поэтому угол Δφ — очень малый угол. Для малых углов выполняется приближенное равенство:
sin Δφ/2 ~ Δφ/2(5)
С учетом (1.5) равенство (4) преобразуется следующим образом:
(Ti+1 + Ti-1)Δφ/2 = Ni(6)
Т. к. уголочень мал, можно принять cos Δφ/2 ~ 1 и преобразовать уравнение (3):
T i +1 — T i -1 = F тр i (7)
Обозначим ΔТ = Тi+1 + Ti-1 — увеличение силы натяжения нити на данном элементе и подставим в (6) и (7):
ΔT = Fтр i(8)
(2Ti-1 + ΔT) Δφ/2 = Ni(9)
Если в уравнении (9) раскрыть скобки, то получим второе слагаемое ΔTΔφ второго порядка малости по малому углу Δφ. Поскольку второе слагаемое много меньше первого, то им можно пренебречь и уравнение (9) трансформируется:
Ti-1 Δφ = Ni(10)
Зная связь силы трения скольжения и силы реакции опоры из (8) и (9) получаем:
μ Ti-1 Δφ = ΔT(11)
Если мы в пределе перейдем к бесконечно малым величинам, то из (11) получаем дифференциальное уравнение:
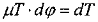
Решается это уравнение разделением переменных:
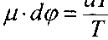
Проинтегрируем по всему углу охвата нитью поверхности φ, при этом сила натяжения нити меняется от T1 до T2 и получим:
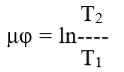
Проведя потенцирование, получаем соотношение силы натяжения нити на «входе» и «выходе» нити с блока в зависимости от угла охвата нитью блока:
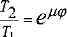
Как видим, чем больше угол охвата нитью блока и коэффициент трения, тем большая сила требуется для движения веревки по блоку. Если рассмотреть идеальный случай, когда трение отсутствует, получим, что силы T1 и T2 равны.
Впервые зависимость силы трения от числа оборотов веревки вокруг сваи установил знаменитый математик XVIII века Леонард Эйлер.
- Экспериментальная часть
Часть 1. Экспериментальная проверка зависимости силы трения нити о поверхность неподвижного цилиндра от диаметра цилиндра
Как можно заметить из формулы (1.15), отношение сил натяжения в крайних местах касания нити о цилиндр не зависит от диаметра самого цилиндра. Чтобы это проверить, достаточно взять цилиндры с одинаковыми поверхностями, но разного диаметра и измерить силы Т1иТ2 в крайних местах касания нити о цилиндр.
В опыте предлагаем использовать установку, представленную на рисунке 4. Цилиндр должен быть неподвижным, нить достаточно легкая по сравнению с грузом.

Рис. 4. Экспериментальная установка
На рис. 5 показаны силы, действующие на цилиндр (1), груз (3), динамометр (4). Рассмотрим силы, с которыми нить действует на тела системы: Т1 приложена к грузу, Т2 к динамометру, Т1’ и Т2’ к цилиндру. Так как нить невесома и нерастяжима, то на вертикальных участках сила натяжения нити во всех сечениях одинакова, поэтому Т1 = Т1’ и Т2 = Т2’.
На поверхность цилиндра действует также сила трения скольжения со стороны нити, она не показана на рис. 5, т. к. направление будет различным для каждого элемента дуги: сила трения, действующая на любой элемент, направлена по касательной к поверхности.
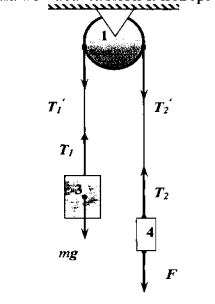
Рис. 5. Схема экспериментальной установки
Запишем второй закон Ньютона для груза.
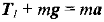
В проекции на вертикальную ось:
T 1 — mg = ma
И если движение равномерное, то T1 = mg, то есть сила натяжения нити на левом крае равна весу груза.
Прикрепив к одному концу нити груз, очень медленно приводим его в движение. Нам необходимо, чтобы ускорение системы было равно нулю (а = 0), следовательно, груз должен двигаться равномерно. Добиться равномерного движения достаточно сложно, поэтому предлагаем, прежде чем проводить основную серию опытов, предварительно потренироваться приводить систему в движение с помощью динамометра.
Силу натяжения на правом крае показывает динамометр:
T 2 ’ = T 2 = F
Угол обхвата нити можно менять с шагом π, но при этом при углах π, 3π, 5π динамометр тянем вниз, а при углах 2π и 4π динамометр тянем вверх, как показано на фотографиях (рис.6, рис.7).

Рис. 6

Рис. 7
Часть 2. Измерение коэффициента трения нити о поверхность цилиндра
Во второй части работы мы предлагаем проверить формулу Эйлера (15) и определить коэффициент трения одной и той же нити о различные поверхности цилиндров.
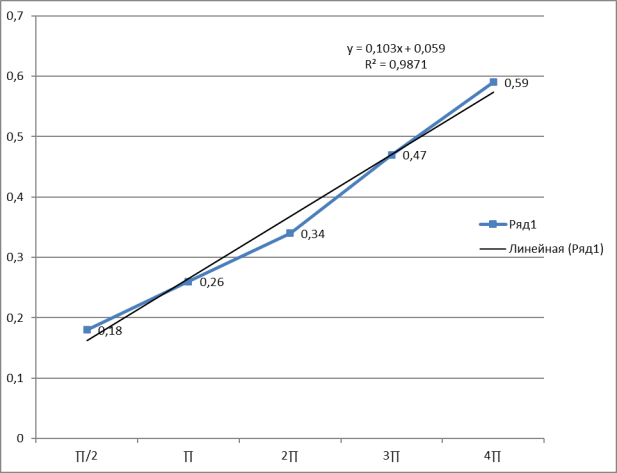
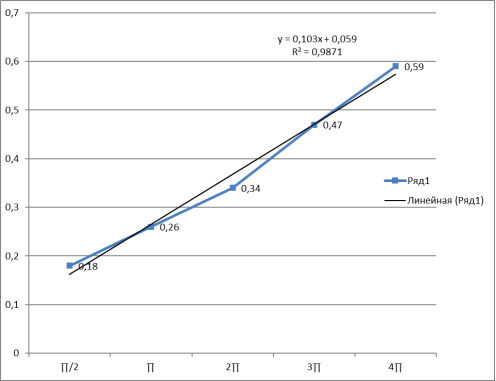
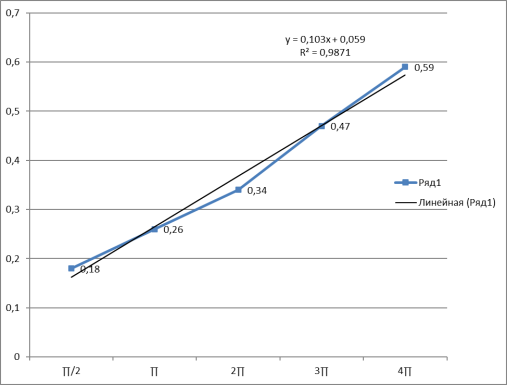
Получив результаты измерений силы натяжения нити Т динамометром, а также зная вес груза Р и угол охвата нитью цилиндра φ, можно проверить (14), что зависимость ln(Т/Р) от угла охвата φ является линейной и определить коэффициент трения нити о цилиндр как коэффициент полученной линейной зависимости.
Указание: если недостаточно шкалы имеющегося динамометра для проведения опытов с различными углами, можно изменять массу поднимаемого груза. Можно в качестве груза использовать ведерко с песком и, досыпая песок, изменять массу.
Экспериментальная установка и методика измерений такая же, как в части 1. Для каждого угла несколько раз измеряем динамометром силу натяжения нити Т при различных значениях веса груза Р, результаты заносим в таблицу 1.1. Значение Tср определяем как среднее арифметическое измеренных величин
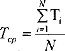
где N — количество измерений.
Можно полученные данные обработать в Ехсе1. Построить график зависимости ln(Tср/Р) от угла охвата нити φ, добавить линию тренда, найти угловой коэффициент, который и будет являться коэффициентом трения нити о поверхность цилиндра. Проверьте коэффициент корреляции R, чтобы подтвердить, что полученная зависимость является линейной. Возможности Ехсе1 позволяют рассчитать и погрешность полученного коэффициента.
Экспериментальная проверка зависимости силы трения нити о поверхность неподвижного цилиндра
Стеклянный цилиндр объемом 1 л
|
Угол (рад) |
m ( г ) |
P ( Н ) |
T ( Н ) |
T ср (Н) |
T ср/ P |
Ln( Тср/ P) | ||
|
1 |
2 |
3 | ||||||
|
|
100 |
0.98 |
1.18 |
1.2 |
1.2 |
1.2 |
1.2 |
0.18 |
|
150 |
1.47 |
1.8 |
1.8 |
1.8 |
1.8 |
1.2 |
0.18 | |
|
200 |
1.96 |
2.4 |
2.4 |
2.4 |
2.4 |
1.2 |
0.18 | |
|
|
100 |
0.98 |
1.3 |
1.3 |
1.3 |
1.3 |
1.3 |
0.26 |
|
150 |
1.47 |
2 |
2 |
2 |
2 |
1.3 |
0.26 | |
|
200 |
1.96 |
2.7 |
2.7 |
2.7 |
2.7 |
1.3 |
0.26 | |
|
|
100 |
0.98 |
1.4 |
1.4 |
1.4 |
1.4 |
1.4 |
0.34 |
|
150 |
1.47 |
2.1 |
2.1 |
2.1 |
2.1 |
1.4 |
0.34 | |
|
200 |
1.96 |
2.9 |
2.9 |
2.9 |
2.9 |
1.4 |
0.34 | |
|
|
100 |
0.98 |
1.6 |
1.6 |
1.6 |
1.6 |
1.6 |
0.47 |
|
150 |
1.47 |
2.4 |
2.4 |
2.4 |
2.4 |
1.6 |
0.47 | |
|
200 |
1.96 |
3.2 |
3.2 |
3.2 |
3.2 |
1.6 |
0.47 | |
|
|
100 |
0.98 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
0.59 |
|
150 |
1.47 |
2.7 |
2.7 |
2.7 |
2.7 |
1.8 |
0.59 | |
|
200 |
1.96 |
3.5 |
3.5 |
3.5 |
3.5 |
1.8 |
0.59 | |
Вывод:
- Из таблицы видно, что сила трения нити о поверхность стеклянного неподвижного цилиндр не зависит от диаметра цилиндра.
- Полученные данные обработаны в Ехсе1. Построен график зависимости ln(Tср/Р) от угла охвата нити φ, добавлена линия тренда, и найден угловой коэффициент, который и будет являться коэффициентом трения нити о поверхность цилиндра.

Стеклянный цилиндр объемом 2 л
|
Угол (рад) |
m ( г ) |
P ( Н ) |
T ( Н ) |
T ср (Н) |
T ср/ P |
Ln( Тср/ P) | ||
|
1 |
2 |
3 | ||||||
|
|
100 |
0.98 |
1.18 |
1.2 |
1.2 |
1.2 |
1.2 |
0.18 |
|
150 |
1.47 |
1.8 |
1.8 |
1.8 |
1.8 |
1.2 |
0.18 | |
|
200 |
1.96 |
2.4 |
2.4 |
2.4 |
2.4 |
1.2 |
0.18 | |
|
|
100 |
0.98 |
1.3 |
1.3 |
1.3 |
1.3 |
1.3 |
0.26 |
|
150 |
1.47 |
2 |
2 |
2 |
2 |
1.3 |
0.26 | |
|
200 |
1.96 |
2.7 |
2.7 |
2.7 |
2.7 |
1.3 |
0.26 | |
|
|
100 |
0.98 |
1.4 |
1.4 |
1.4 |
1.4 |
1.4 |
0.34 |
|
150 |
1.47 |
2.1 |
2.1 |
2.1 |
2.1 |
1.4 |
0.34 | |
|
200 |
1.96 |
2.9 |
2.9 |
2.9 |
2.9 |
1.4 |
0.34 | |
|
|
100 |
0.98 |
1.6 |
1.6 |
1.6 |
1.6 |
1.6 |
0.47 |
|
150 |
1.47 |
2.4 |
2.4 |
2.4 |
2.4 |
1.6 |
0.47 | |
|
200 |
1.96 |
3.2 |
3.2 |
3.2 |
3.2 |
1.6 |
0.47 | |
|
|
100 |
0.98 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
0.59 |
|
150 |
1.47 |
2.7 |
2.7 |
2.7 |
2.7 |
1.8 |
0.59 | |
|
200 |
1.96 |
3.5 |
3.5 |
3.5 |
3.5 |
1.8 |
0.59 | |
Вывод:
- Из таблицы видно, что сила трения нити о поверхность стеклянного неподвижного цилиндр не зависит от диаметра цилиндра.
- Полученные данные обработаны в Ехсе1. Построен график зависимости ln(Tср/Р) от угла охвата нити φ, добавлена линия тренда, и найден угловой коэффициент, который и будет являться коэффициентом трения нити о поверхность цилиндра.

Стеклянный цилиндр объемом 3 л
|
Угол (рад) |
m ( г ) |
P ( Н ) |
T ( Н ) |
T ср (Н) |
T ср/ P |
Ln( Тср/ P) | ||
|
1 |
2 |
3 | ||||||
|
|
100 |
0.98 |
1.18 |
1.2 |
1.2 |
1.2 |
1.2 |
0.18 |
|
150 |
1.47 |
1.8 |
1.8 |
1.8 |
1.8 |
1.2 |
0.18 | |
|
200 |
1.96 |
2.4 |
2.4 |
2.4 |
2.4 |
1.2 |
0.18 | |
|
|
100 |
0.98 |
1.3 |
1.3 |
1.3 |
1.3 |
1.3 |
0.26 |
|
150 |
1.47 |
2 |
2 |
2 |
2 |
1.3 |
0.26 | |
|
200 |
1.96 |
2.7 |
2.7 |
2.7 |
2.7 |
1.3 |
0.26 | |
|
|
100 |
0.98 |
1.4 |
1.4 |
1.4 |
1.4 |
1.4 |
0.34 |
|
150 |
1.47 |
2.1 |
2.1 |
2.1 |
2.1 |
1.4 |
0.34 | |
|
200 |
1.96 |
2.9 |
2.9 |
2.9 |
2.9 |
1.4 |
0.34 | |
|
|
100 |
0.98 |
1.6 |
1.6 |
1.6 |
1.6 |
1.6 |
0.47 |
|
150 |
1.47 |
2.4 |
2.4 |
2.4 |
2.4 |
1.6 |
0.47 | |
|
200 |
1.96 |
3.2 |
3.2 |
3.2 |
3.2 |
1.6 |
0.47 | |
|
|
100 |
0.98 |
1.8 |
1.8 |
1.8 |
1.8 |
1.8 |
0.59 |
|
150 |
1.47 |
2.7 |
2.7 |
2.7 |
2.7 |
1.8 |
0.59 | |
|
200 |
1.96 |
3.5 |
3.5 |
3.5 |
3.5 |
1.8 |
0.59 | |
Вывод:
- Из таблицы видно, что сила трения нити о поверхность стеклянного неподвижного цилиндр не зависит от диаметра цилиндра.
- Полученные данные обработаны в Ехсе1. Построен график зависимости ln(Tср/Р) от угла охвата нити φ, добавлена линия тренда, и найден угловой коэффициент, который и будет являться коэффициентом трения нити о поверхность цилиндра.

Выводы:
- T2 / T1, а, следовательно сила трения нити о поверхность неподвижного цилиндра не зависит от диаметра цилиндра.
- Чем больше угол охвата нитью блока, тем большая сила трения требуется для движения веревки по блоку.
- Чем больше коэффициент трения, тем большая сила требуется движения веревки по блоку.
- Зависимость логарифма отношения T/P от угла охвата φ является линейной.
- Коэффициент трения определяется как тангенс угла наклона.

Литература:
1. Тихонов Павел Сергеевич. Курс «Экспериментальный тур олимпиад по физике»
- Квант» 1988 год номер 5 Научно-популярный физико-математический журнал «Квант» (издается с января 1970 года)
- Л. П. Лисовский. «Трение в природе и технике», журн. «Квант».
- Дерягин Б. В. Что такое трение? М.: Изд. АН СССР, 1963.
- Крагельский И. В., Щедров В. С. Развитие науки о трении. Сухое трение. М.: Изд. АН СССР, 1956.
- Фролов, К. В. (ред.) Современная трибология: Итоги и перспективы. ЛКИ, 2008.
- Силин А. А. «Трение и мы» 1987.
- Р. Фейнман, Р. Лейтон, М. Сендс “Фейнмановские лекции по физике” 1976г.
- “Элементарный учебник физики” под ред. Академика Г. С. Ландсберга 1971г.
- Перельман Я. И. “Занимательная физика” 1999г.