Статистическая модель системы факторов размещения грузовых объектов на сети железных дорог Узбекистана



В данной статье произведен кластерный анализ регионов потенциального размещения логистических центров, субъекты Узбекистана разделены на четыре кластера в зависимости от уровня их социально-экономического, инфраструктурного развития, особенностей географического положения и объему выполняемой транспортной работы. Регионы Узбекистана были сгруппированы по кластерам в зависимости от таких показателей как численность населения, среднедушевые доходы населения, объем ВРП, объем промышленного производства, объем экспортной продукции, плотность железнодорожных путей, плотность автомобильных дорог, принадлежность к климатической зоне.

Ключевые слова: склад, размещение грузовых объектов, статистическая модель, кластер, кластерный анализ, наименьшее расстояние.

In this article, a cluster analysis is made, the regions of potential placement of logistics centers, the subjects of Uzbekistan are divided into four clusters depending on the level of their socio-economic, infrastructural development, geographical location and the volume of transport work performed. The regions of Uzbekistan were grouped into clusters depending on such indicators as population, per capita income, GRP, industrial production, exports, railway density, road density, climate zone.

Keywords: warehouse, placement of cargo objects, statistical model, cluster, cluster analysis, smallest distance.

Введение. При решении задачи оптимального размещения грузовых объектов на сети железных дорог с целью обеспечения логистическими мощностями имеющиеся и формирующиеся промышленно-обрабатывающие кластеры требуется найти такое месторасположение распределительных центров или площадок относительно своих поставщиков и потребителей, при котором некая целевая функция суммарных логистических затрат, достигает своего минимального значения при комплексном учете всех значимых влияющих факторов. Математически эта задача служит цели многокритериальной оптимизации при наличии системы ограничений.

Методы исследования. Первоначально задача оптимального расположения грузового объекта с возможностью погрузки и складирования должна учитывать такие основные факторы, как расстояния между складом и поставщиками и потребителями, объемы перевозимых грузов, транспортные тарифы и время доставки грузов от поставщиков на склад и со склада потребителям, и решаться определением координат (x, y) грузового объекта так, чтобы логистические издержки, равные сумме произведений расстояний от поставщиков до грузового объекта и от грузового объекта до пункта назначения, имеющего координаты (x _i , y _i ), на объемы перевозимых грузов Q _i (потребность или спрос), были минимальны, так как показано формулой 1:

, (1)

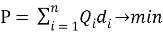
где: — расстояние от грузового объекта до i-го поставщика или до пункта назначения (i=1, 2, … n).

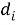
Если задачу укрупнить до уровня расположения распределительных логистических центров на территории страны, то следует разбить процедуру разработки модели на несколько этапов [5], как показано на рис. 1.

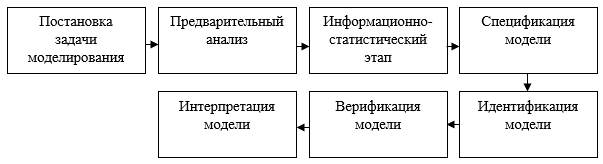
Рис. 1. Основные этапы построения статистической модели

Для определения уровня зависимости между факторами влияния на размещение логистических центров проводится оценка значений зависимых (эндогенных) переменных у ₁ , у ₂ , … у _m в зависимости от значений независимых (экзогенных) переменных х ₁ , х ₂ , … х _k с учетом влияния не поддающихся измерению случайных компонентов 1, 2, … m (влияние не включенных в модель факторов и случайных ошибок в измерении показателей) [6].

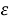
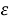
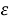
К экзогенным или независимым переменным статистической модели относятся: климатическая зона, обеспеченность автомобильными дорогами и железнодорожными путями, наличие транспортных коридоров на территории региона, численность населения.

Остальные переменные определяются как зависимые (эндогенные).

Таким образом, статистически описывающая и позволяющая оценить изменение во времени и в пространстве системы факторов размещения логистических центров массив данных состоит из Р факторов по N регионам Узбекистана за Т временных интервалов [7], как показано на рис. 2.

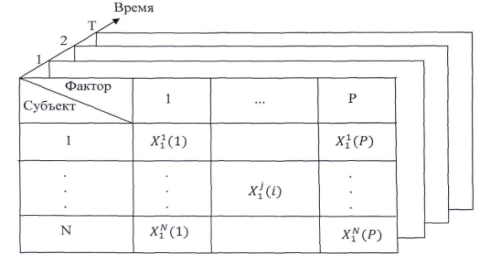
Рис. 2. Графическое представление рассматриваемой структуры данных

Предварительный анализ показал, что имеющиеся в Узбекистане логистические центры размещены в регионах, имеющих высокие значения развития торговли и промышленности, численности населения и выгодное географическое расположение в отношении сухопутных транспортных коридоров.

Оценка системы факторов размещения логистических центров проводилась на основе пространственно-временной выборки (17 показателей по 13 регионам (город Ташкент из выборки исключен в связи с достаточной обеспеченностью логистическими центрами), период исследования 2010–2022 годы), на основе данных Государственного комитета Республики Узбекистан по статистике [8].

Показатели включаются в статистическую модель с различными коэффициентами регрессии, значения которых зависят от принадлежности региона к определенному кластеру. Для получения более точных коэффициентов регрессии и учета влияния принадлежности региона Узбекистана к определенному кластеру вводятся фиктивные переменные:

Модель зависимости i -го фактора имеет вид:

, (3)

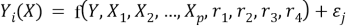
где: i — случайная компонента.

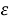
Форма зависимости i -го показателя ( Y _i ) от Х имеет вид:

Yi(X) = β0 + ∑αk*rk, + ∑ β j* Х j, + εj(4)

где: X _j — значение j переменной, имеющей наиболее сильное влияние на i показатель;

0 и j — неизвестные коэффициенты уравнения регрессии;

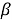
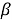
r _k — фиктивная переменная, где k — номер кластера;

r _k — коэффициент регрессии при фиктивной переменной.

Для оценки параметров уравнения регрессии используется множественный регрессионный анализ, так как количество переменных, от которых зависит j — й показатель больше одного [7].

Для группировки многомерных объектов и представления результатов отдельных наблюдений точками подходящего геометрического пространства с последующим выделением групп как кластеров производится кластерный анализ с использованием различных программных комплексов (например, Statistica) [9]. Объекты, входящие в определенный кластер, обладают сходными свойствами.

Сходство с другими объектами определяется как соответствующее расстояние между объектами в пространстве называется, то есть величина d _ab , удовлетворяющая аксиомам [10]:

(5)

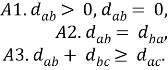
Как меру расстояния целесообразно использовать геометрическое расстояние между двумя точками в многомерном пространстве, то есть евклидово расстояние:

, (6)

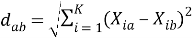
где: X _ia , X _ib значения i -го признака у a-го (b-го) объекта (i = 1,2,..., k, а, b = 1, 2, … n ).

Кластерный анализ проводился с помощью программы Exsel. Все показатели нормируются посредством отношения разницы исходного и среднеарифметического значения показателей к среднеквадратичному отклонению (в созданной модели данная вкладка называется «Кластерный анализ»).

Далее получившиеся выделяются данные и с помощью алгоритма Вставка-Сводная таблица открываются в новом листе (в созданной модели данная вкладка называется «Наименьшие расстояния»). Здесь параметр «регионы» переносится в столбцы, в строки переносится параметр «номер региона» (№ пп) по выбранному значению «Объем грузовых железнодорожных перевозок» (Vпер.жд, млн.т) с выставлением параметров полей значения «Максимум по полю».

Заранее выбрав в качестве k (число кластеров) значение 4, задаются формулы по получившимся массивам данных, выделяя такие факторы, как расстояние до каждого кластера, наименьшее расстояние, номер кластера, количество регионов в каждом кластере. Выставляется целевая функция (сумма наименьших расстояний). Используется инструмент «Поиск решения» во вкладке «Данные», где в качестве ограничений значений выбирается 0 ≤ k ≤ 1 с поиском наименьшего значения. Используется метод — «Эволюционный поиск решения». Получившиеся данные разбиваются с помощью инструмента «Цветовая шкала» во вкладке «Условное форматирование», регионы каждого кластера классифицируются по общности данных.

В результате проведенного кластерного анализа выделено 4 кластера:

1 кластер — Хорезмская область;

2 кластер — Самаркандская область;

3 кластер — Республика Каракалпакстан, Андижанская область, Бухарская область, Джизакская область, Кашкадарьинская область, Навоийская область, Сурхандарьинская область, Сырдарьинская область, Ташкентская область, Ферганская область.

4 кластер — Наманганская область.

Заключение

В результате исследования комплекса моделей формирования грузовых объектов были сформулированы следующие выводы:

Предварительная оценка регионов Республики Узбекистан показала необходимость транспортного инфраструктурного развития в таких регионах как Хорезмская и Кашкадарьинская области и реализации намеченных планов по логистическому обеспечению, включая размещение грузовых объектов на сети железных дорог в таких областях как Андижанская, Ферганская, Самаркандская, Бухарская, Сырдарьинская и Джизакская, а также в Республике Каракалпакстан. Особенно остро стоит вопрос транспортного обеспечения производственно-торговой логистики в Хорезмской области.

В результате проведенного кластерного анализа регионов потенциального размещения логистических центров субъекты Узбекистана разделены на четыре кластера в зависимости от уровня их социально-экономического, инфраструктурного развития, особенностей географического положения и объему выполняемой транспортной работы. Регионы Узбекистана были сгруппированы по кластерам в зависимости от таких показателей, как численность населения, среднедушевые доходы населения, объем ВРП, объем промышленного производства, объем экспортной продукции, плотность железнодорожных путей, плотность автомобильных дорог, принадлежность к климатической зоне. К первому кластеру отнесена Хорезмская область, ко второму — Самаркандская область, к четвертому — Наманганская, остальные регионы относятся к третьему кластеру.

Литература:

1. Мухамедова З. Г., Ибрагимова Г. Р. К вопросу формирования грузовой инфраструктуры Республики Узбекистан / Известия Транссиба. — 2022. — № 1 (49). — С.59–66.
2. Мухаммедова З. Г., Эргашева З. В., Асатов Э. А. К вопросу о развитии транспортной инфраструктуры Узбекистана/ Известия Транссиба. — 2021. — № 2 (46). — С.105.
3. Мухамедова, З. Г. К вопросу формирования грузовой инфраструктуры Республики Узбекистан / Мухамедова З. Г., Ибрагимова Г. Р. // Известия Транссиба. — 2022. — № 1 (49). — С. 57–67.
4. Makhkamov N. Y. The rational connection coefficient calculation with different train structures. / Makhkamov N. Y., Ibragimova G. R., Ismatullaev A. F. // В сборнике: IOP Conference Series: Materials Science and Engineering. 8. Сер. «VIII International Scientific Conference Transport of Siberia 2020" 2020. С. 012052.
5. Сай, В. М. Интегрированный коэффициент эффективности проектов при взаимодействии ОАО «РЖД» с региональными хозяйствующими субъектами/В. М. Сай//Транспорт Урала. — 2015. — № 4. — С.7–14.
6. Хайруллина, О.И., Баянова, О. В. Эконометрика/О. И. Хайруллина, О. В. Баянова. — Пермь: 2019, 176 с.
7. Иванова, Т. А. Методы исследования социально-экономических и демографических процессов / Т. А. Иванова, К. Ю. Дорогина, И. Н. Попова, Ю. Д. Дружинина. — Магнитогорск: ФГБОУ ВПО «Магнитогорск, гос. Техн. Ун-та им. Г. И. Носова», 2012. — 155 с.
8. Официальный сайт Государственного комитета Республики Узбекистан по статистике [Электронный ресурс]. — URL: https://www.stat.uz/ru/ofitsialnaya-statistika/investments (дата обращения: 11.03.2022).
9. Сай, В.М., Сизый, С.В., Фомин, В. К. Интегральная оценка предприятий / В. М. Сай, С. В. Сизый, В. К. Фомин // Экономика железных дорог. — 2010. — № 1. — С.16–33.
10. Буреева, Н. Н. Многомерный статистический анализ с использованием «STATISTICA». Учебно-методический материал / Н. Н. Буреева. — Нижний Новгород, 2007.-112 с.