Метод расчета дополнительных потерь активной мощности в электрической сети от высших гармоник тока

В статье автор приводит математическую модель для расчета коэффициента увеличения активного сопротивления проводника воздушной линии.

Ключевые слова: высшие гармоники, потери активной мощности, воздушные линии.

При протекании по жилам проводов и кабелей переменных токов в них наблюдается скин-эффект — вытеснение тока к поверхности проводника. Точные математические выражения, описывающие влияние частоты электрического тока на сопротивление токопроводящей жилы даны в теории электромагнитного поля [1].

Расчеты по формуле Гераскина для воздушных линий

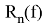
Для воздушных линий (ВЛ) электропередач, провода которых имеют витую многопроволочную конструкцию, зависимость существенно нелинейна; на значения активного сопротивления влияют поверхностный эффект и эффект близости, проводимость земли, а для сталеалюминиевых проводов — наличие стального троса.

Авторами [2] найдены зависимости:

(1.1)

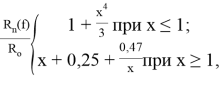
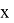
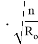
где = 0,1 — промежуточный параметр, используемый в расчетах.

Осуществим расчет для воздушной линии, выполненной из алюминия сечением 120 мм2, для остальных сечений расчет аналогичен.

= 0,1 = 0,1 ∙ = 0.202 о.е.

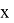
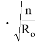
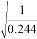
Коэффициент увеличения сопротивления из системы уравнений 1.1 будет определяться по формуле

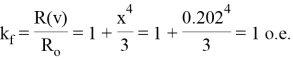
Таблица 1

Линия сечением 120 мм 2

№ гармоник	1	2	3	5	7	9	11	13	15	17	21
f, Гц	50	100	150	250	350	450	550	650	750	850	1050
Rо Ом/км	0,244	0,244	0,244	0,244	0,244	0,244	0,244	0,244	0,244	0,244	0,244
Kf o. e.	1	1,002	1,005	1,014	1,027	1,045	1,068	1,095	1,126	1,162	1,247
Rn Ом/км	0,244	0,245	0,245	0,247	0,251	0,255	0,261	0,267	0,275	0,283	0,304

Таблица 2

Линия сечением 150 мм 2

№ гармоник	1	2	3	5	7	9	11	13	15	17	21
f, Гц	50	100	150	250	350	450	550	650	750	850	1050
Rо Ом/км	0,204	0,204	0,204	0,204	0,204	0,204	0,204	0,204	0,204	0,204	0,204
Kf o. e.	1	1,003	1,007	1,020	1,039	1,065	1,097	1,135	1,180	1,231	1,353
Rn Ом/км	0,204	0,205	0,205	0,208	0,212	0,217	0,224	0,232	0,241	0,251	0,276

Таблица 3

Линия сечением 240 мм 2

№ гармоник	1	2	3	5	7	9	11	13	15	17	21
f, Гц	50	100	150	250	350	450	550	650	750	850	1050
Rо Ом/км	0,118	0,118	0,118	0,118	0,118	0,118	0,118	0,118	0,118	0,118	0,118
Kf o. e.	1	1,010	1,022	1,060	1,117	1,194	1,290	1,405	1,539	1,692	2,056
Rn Ом/км	0,118	0,119	0,121	0,125	0,132	0,141	0,152	0,166	0,182	0,200	0,243

Таблица 4

Линия сечением 300 мм 2

№ гармоник	1	2	3	5	7	9	11	13	15	17	21
f, Гц	50	100	150	250	350	450	550	650	750	850	1050
Rо Ом/км	0,096	0,096	0,096	0,096	0,096	0,096	0,096	0,096	0,096	0,096	0,096
Kf o. e.	1	1,014	1,033	1,090	1,177	1,293	1,438	1,611	1,814	2,045	2,595
Rn Ом/км	0,096	0,097	0,099	0,105	0,113	0,124	0,138	0,155	0,174	0,196	0,249

Таблица 5

Линия сечением 400 мм 2

№ гармоник	1	2	3	5	7	9	11	13	15	17	21
f, Гц	50	100	150	250	350	450	550	650	750	850	1050
Rо Ом/км	0,073	0,073	0,073	0,073	0,073	0,073	0,073	0,073	0,073	0,073	0,073
Kf o. e.	1	1,025	1,056	1,156	1,306	1,507	1,757	2,057	2,407	2,808	3,758
Rn Ом/км	0,073	0,075	0,077	0,084	0,095	0,110	0,128	0,150	0,176	0,205	0,274

Построим зависимость относительного коэффициента увеличения сопротивления от частоты гармоники.

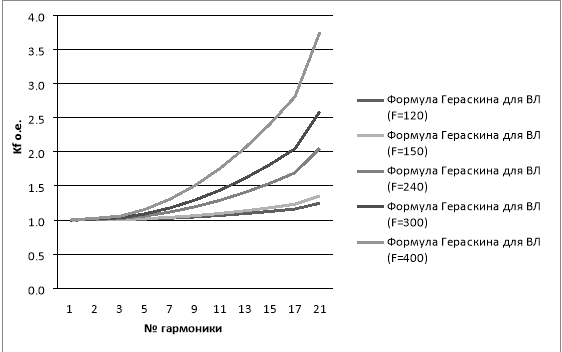
Зависимость коэффициента увеличения сопротивления от частоты гармоник

Рис. 1. Зависимость коэффициента увеличения сопротивления от частоты гармоник

Расчет сопротивлений для приоритетных гармоник зависит от изменения частоты, поэтому необходимо пересчитать полученные значения на основной частоте

𝑅𝑛(𝑓) = 𝑘𝑓 ∙ 𝑅,

(1. 2)

где 𝑘𝑓 — коэффициент увеличения активного сопротивления, определяемый по таблице 1.1–1.5;

R — активное сопротивление кабеля для участка сети.

Согласно [3], дополнительные потери активной мощности в проводнике, вызванные протеканием высших гармоник тока, могут быть определены по формуле

(1.3)

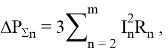
где n — номер гармоники; 𝐼𝑛 — ток n-ой гармоники, А; 𝑅𝑛 — активное сопротивление n-й гармоники, Ом; m — число учитываемых гармоник.

Потери активной мощности для основной частоты вычисляются по общеизвестной формуле

(1.4)

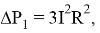
Тогда по принципу суперпозиции суммарные потери для электрической сети будут вычисляться

= 3 ∙ ( + ). (1.5)

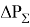
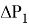
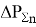
Выводы:

1. Эффект вытеснения тока к поверхности проводника для различных гармоник имеет разное значение. Наиболее удобно выражать это явление с помощью коэффициента увеличения активного сопротивления по отношению к омическому сопротивлению или по отношению к активному сопротивлению на основной частоте переменного тока 50 Гц.

2. Учет потерь активной мощности от гармонических составляющих необходимо обязательно учитывать, что даст поправку, от 20 % до 50 % к потерям, вычисленным на основной частоте.

Литература:

Бессонов Л. А. Теоретические основы электротехники: электромагнитное поле / Л. А. Бессонов. — 10-е изд., перераб. и доп. — М.: Гардарики, 2007. — 317 с
Гераскин О. Т. Применение вычислительной техники для расчета высших гармоник в электрических сетях. / О. Т. Гераскин, В. В. Черепанов. — М.: ВИПКЭнерго, 1987. — 300 с.
Жежеленко И. В. Электрические потери от высших гармоник в системах электроснабжения / И. В. Жежеленко // Электрика –2010. — № 4. — С.3–6.

Молодой учёный

Метод расчета дополнительных потерь активной мощности в электрической сети от высших гармоник тока

Метод расчета дополнительных потерь активной мощности в электрической сети от высших гармоник тока

Молодой учёный