К вопросу об определении динамического эффекта в статических расчетах прогрессирующего обрушения



В статье рассматривается подход к определению значения динамического коэффициента для квазистатического подхода к расчету на прогрессирующее обрушение зданий или сооружений. Количественная величина влияния оценивается на примере плоской рамной стержневой системы путем сравнения результатов расчета в статической и физически-нелинейной динамической постановках. В заключении приводятся рекомендации по назначению более приближенного к реальной работе коэффициента динамичности.

Ключевые слова: прогрессирующее обрушение, коэффициент динамичности, нелинейный статический расчет, пластические шарниры, нелинейный динамический расчет.

Одной из главных задач при проектировании зданий и сооружений является обеспечение безопасности проектируемого объекта. Существует множество методик, которые направлены на увеличение надежности зданий и сооружений. Одной из таких методик является расчет на прогрессирующее обрушение, которое регламентируется отечественным сводом правил [1], вступившем в силу в 2019 году.

Прогрессирующее (лавинообразное) обрушение — последовательное (цепное) разрешение несущих строительных конструкций, приводящее к обрушению всего здания или сооружения, или его частей вследствие начального локального разрушения [1].

Данный расчет необходимо применять при проектировании зданий и сооружений класса КС-3, а также зданий и сооружений класса КС-2 с массовым нахождением людей [2].

Отечественной нормативной документацией предусмотрено несколько методов расчета зданий и сооружений на прогрессирующее обрушение.

Расчет кинематическим методом теории предельного равновесия включает следующие этапы:

— Включение в расчётную схему всевозможных механизмов разрушения и пластических шарниров, находя обобщённые перемещения по направлению усилий после отказа несущего элемента.

Согласно пункту 7.10 [1] данный метод применяется при обеспечении пластической работы системы в предельном состоянии.

Расчет в динамической постановке позволяет определить напряженно-деформированное состояние в каждый отдельно взятый период времени с помощью выполнения множество итераций расчета на определенном промежутки времени. Данный метод позволяет наиболее точно приблизить результаты расчета к реальности. Но с другой стороны методика требует сложной настройки расчетной схемы и большего количества времени на расчет из-за высокой потребности в вычислительных мощностях, что в условиях проектирования может вызвать проблемы.

Расчет в статической постановке довольно часто применяется на практике, так как эта методика является наименее трудоемкой в плане настройки расчетной схемы и потребления вычислительных мощностей, что позволяет в условиях реального проектирования оперативно рассматривать различные аварийные ситуации. Суть данной методики заключается в определении напряженно-деформированного состояния расчетной схемы с последующим выключением одного из несущих элементов и прикладыванием ранее определенных усилий прикрепления данного элемента с обратным знаком. Прикладывания усилий прикрепления с обратным знаком это имитация динамического эффекта от мгновенного удаления несущего элемента расчетной схемы. В свою очередь дополнительные усилия от динамического эффекта в данной методики учитываются с помощью коэффициента динамичности . Из курса строительной механики известно, что при мгновенном приложении нагрузки коэффициент динамичности =2, а при статическом =1.

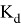
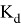
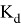
На данный момент в отечественных нормах не указано, какую именно величину необходимо принимать для данного коэффициента, но в предыдущей редакции свода правил [1] значение коэффициента динамичности равнялось 2, что приводило к существенному увеличению металлоемкости.

При рассмотрении реальных расчетных ситуаций абсолютно мгновенного выключения несущего элемента из работы не бывает, а диаграмма работы строительных сталей предполагает нелинейные свойства материалов, что способствует перераспределению напряжений. Вследствие этого =2 кажется чересчур консервативным и возникает потребность в уточнении этого коэффициента в статической постановке для получения результатов расчета наиболее близких к реальности как при динамическом расчете, но затрачивая на это минимальное количество времени и ресурсов.

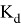
Рассмотрим плоскую раму, представленную на рисунке 1, в которой колонны сечением I35Ш1, а балки 40Ш1. Для выключения из работы выбрана крайняя колонна первого этажа.

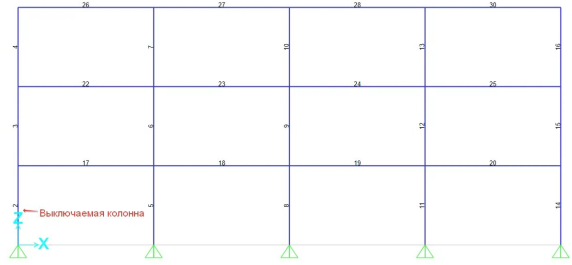
Рис. 1. Расчетная схема

На первом этапе выполняется нелинейный статический и динамические расчеты. В свою очередь расчет в статической постановке выполнен в двух вариантах, когда реакция выключаемой колонны приложена с обратным знаком с коэффициентом динамичности =1 и =2. График момента в ригеле № 17 в сечении над колонной № 5 (см. рисунок 1) при различном приложении нагрузок представлен на рисунке 2. При сравнении моментов в динамической и статических постановках видно, что при мгновенном удалении элемента, что соответствует времени удаления элемента в величину T/10, максимальное значения момента в динамической постановке практически совпадает со значением момента в статической постановке с приложением усилий с коэффициентом динамичности =2. А если время удаления элемента равняется T, то значения момента в динамической постановке совпадает со значением момента в статической постановке с использованием коэффициента динамичности =1. Полученные результаты вполне ожидаемы, и они подтверждают известные закономерности из строительной механики.

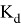
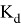
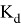
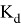
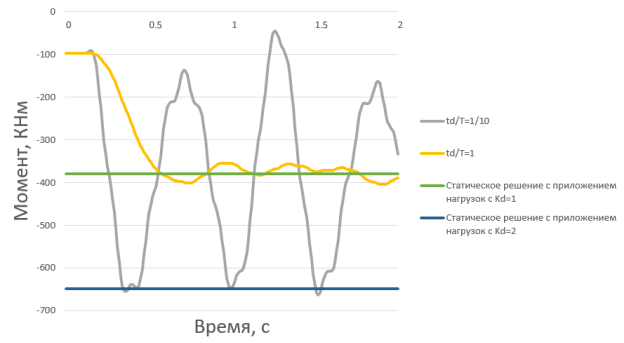
Рис. 2. Диаграмма момента при отказе крайней колонны в статической и динамической постановке

На втором этапе в расчетную схему были введены пластические шарниры, которые расположены в начале и конце конечных элементов. Также было учтено демпфирование равное 2 %. Как видно из рисунка 3 ригели над выключаемой колонной ушли в пластическую зону работы стали (зеленные маркеры на концах конечных элементов). Данная цветовая индексация сигнализирует о том, что материал работает в пластической зоне (зона B-C [3]).

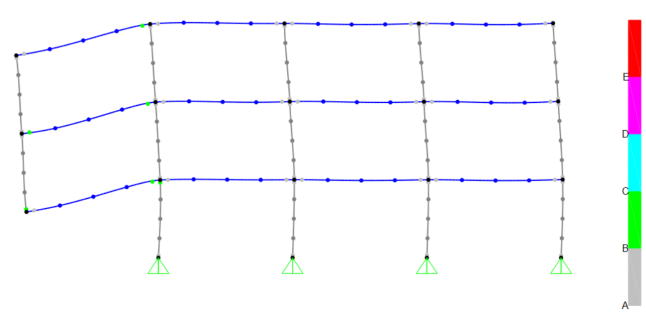
Рис. 3. Деформированная схема с пластическими шарнирами

При сравнении значения момента в точке 1 в динамической постановке с учетом пластической работы стали с результатами, полученными на первом этапе в статической постановке видно, что максимальный момент снизился, и в данном случае коэффициент динамичности соответствует =1.3.

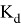
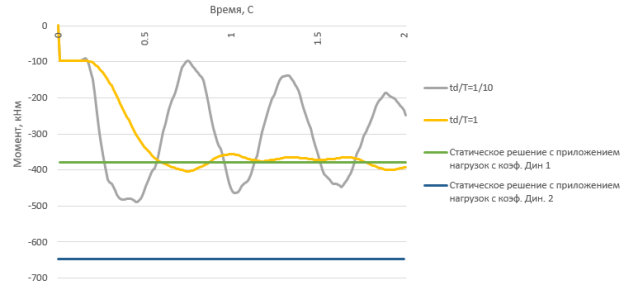
Рис. 4. Диагарамма момента при отказе крайней колонны в статической и динамической постановке с учетом пластической работы стали

Для данной расчетной схемы определяющим фактором для определения коэффициента динамичности является изгибающий момент, но при рассмотрении более сложных расчетных схем следует учитывать также перемещения, крутящие моменты, продольные и поперечные силы.

Подводя итоги, можно сказать, что учет пластической работы стали при расчете на прогрессирующее обрушение, позволяет значительно сэкономить расход металла, так как к деформациям предъявляются более заниженные требования при расчете на особые воздействия. Для подобных рам с жестко защемленными ригелями при расчете на прогрессирующее обрушения в статической постановке в аварийной ситуации, когда рассматривается выключение крайней колоны, можно применять коэффициент динамичности равный 1.3. При дальнейшем рассмотрении вышеизложенной методики рекомендуется проанализировать аварийные ситуации с выключением различных несущих элементов, а также более реальные расчетные схемы, например, связевой каркас, для последующего уточнения коэффициентов динамичности.

Литература:

1. СП 385.1325800.2018 «Защита зданий и сооружений от прогрессирующего обрушения. Правила проектирования. Основные положения (с Изменениями № 1, 2»

2. ГОСТ 27751–2014 «Надежность строительных конструкций и оснований. Основные положения»

3. СП 16.13330.2017 «Стальные конструкции. Актуализированная редакция СНиП II-23–81*» (с Поправками, с Изменениями № 1, 2,3)