Пространственная экстраполяция параметров состояния атмосферы на основе динамико-стохастической модели, учитывающей вертикальную изменчивость метеорологического поля (часть 1)

В статье автор пытается определить принцип работы фильтра Калмана для дальнейшего его применения в предложении методики пространственной экстраполяции параметров состояния атмосферы на основе динамико-стохастической модели, учитывающей вертикальную изменчивость метеорологического поля и сделать общую постановку задачи.

Ключевые слова : фильтр Калмана, пространственная интерполяция, численное моделирование, малопараметрическая динамико-стохастическая модель.

Общая постановка задачи:

Задачей является восстановление вертикального профиля метеовеличины по приземным измерениям.

Пусть в наличии имеется n сеансов измерений вертикального профиля величины: , V _x , V _y , P как f(h, t). График представлен на рис. 1

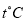
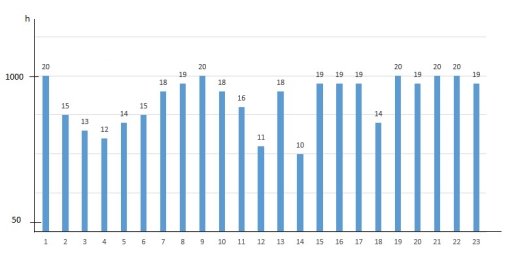
Рис. 1. Вертикальные профили измерений метеовеличины

Каждые 5 минут выполняются контактные измерения до высоты ПАС (1 км). И строится вертикальный профиль. Пример построения вертикального профиля представлен на рис. 2.

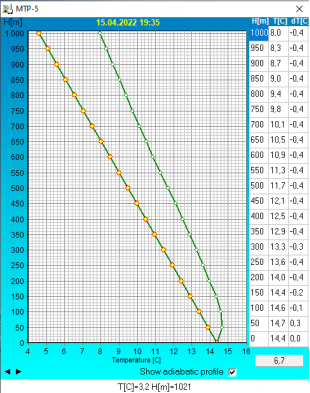
Рис. 2. Вертикальный профиль измерений

Порядок решения задачи

На первом этапе выполняется предварительная оценка и предварительная оценка . На втором этапе выполняется обработка входных данных на предмет оценки экстраполяции вектора метеовеличины. Алгоритм решения задачи представлен на рис. 3.

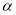
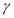
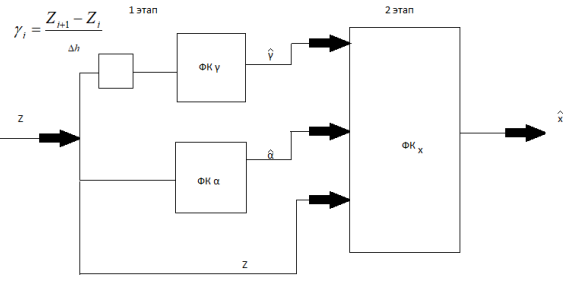
Рис. 3. Алгоритм решения задачи

Для расчета

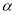
Полагая [1], график представлен на рис. 4.

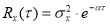
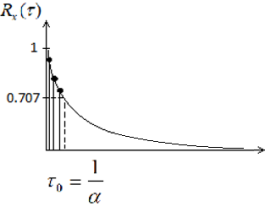
Рис. 4. График автокорреляционной функции

Полагая 1 км = , 50 м = , то количество отсчетов будет N = .

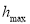
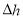
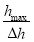
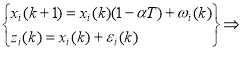
Вектор измерения

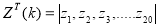
Расчет коэффициента связи между двумя высотными уровнями

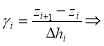
Используя данные температуры, представленные на рис. 5. Произведем расчеты коэффициента связи между двумя высотными уровнями для всех отсчетов.

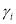
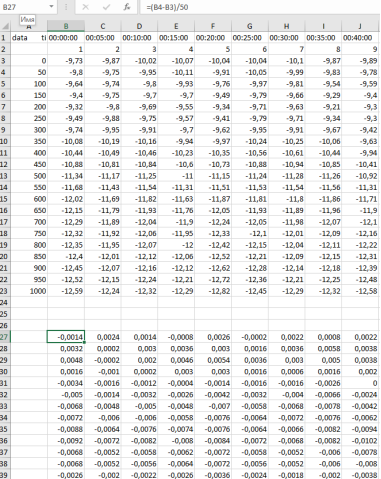
Рис. 5. Входные данные температур и рассчитанные коэффициенты связи

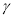
Литература:

1. Комаров В. С., Попов Ю. Б., Суворов С. С., Кураков В. А. Динамикостохастические методы и их применение в прикладной метеорологии / Под общей редакцией Г. Г. Матвиенко. — Томск: Изд-во ИОА СО РАН, 2004. — 236 с.
2. Попов Ю. Б., Попова А. И. Оптимальная фильтрация и её применение для задачи мониторинга параметров состояния атмосферы в рамках локальных территорий. — Ханты-Мансийск: Полиграфист, 2008. — 188 с.