Разумеется при обучении математики задачи несут разные функции: обучающие, воспитывающие, развивающие, контролирующие. Рассмотрим более подробно как можно математическим задачам придать развивающую функцию. Когда говорят о усвоении обучающимися в школе математику, то подразумевают, что должны не только получить знания, навыки, но и самое главное применить эти знания и навыки в нестандартной для обучающегося обстановке. Для этого обязательно ребенок должен пройти через определённого количество определений, формул, теорем, решить определённое количество задач. Но выбирая профиль, мы сталкиваемся с тем, что количество часов меняется от 9 часов в неделю до 4 часов в неделю. Как быть в такой ситуации? Остается надеяться на усиление развивающей функции задач. Можно достичь частичным изменением условия задачи, рассмотрением её частных или предельных случаев, постановкой дополнительных вопросов, решение более рациональным способом и т. д. [1].
Особенно усилить развивающую функцию задач можно при решении нестандартных задач. Способ конечно очень даже отличный, но есть недостаток. Не хватит урока для решения такой задачи. Конечно, можно такие задачи решать после уроков, на внеурочном занятии. Но если нет такого занятия, остаётся использовать обычные задачи, но развивающую функцию математических школьных задач достигать путём постановок дополнительных вопросов. При постановках вопросов обучающимся, как правило, учителя математики просят вспомнить «назовите», «расскажите», «сформулируйте». Память развивать необходимо. Но развивать мышление, а соответственно уметь выстраивать логическую цепочку крайне необходимо в современном мире. Поэтому надо задавать такие вопросы, чтобы провоцировать обучающихся совершать те или иные мыслительные операции и тем самым способствовать развитию мышления.
Возможно рассмотреть следующие виды вопросов, которые помогают осуществлять развивающую функцию задач в обучении математики:
- Вопросы на сравнение.
Например «В чём сходство и различие параллелограмма и ромба?»
- Вопросы которые требуют установления признаков, понятий, следствий.
Например «Является ли признаком ромба перпендикулярность его диагоналей?»
- Вопросы на установление причинно-следственных связей.
Например «Почему в логарифмическом уравнении появляются посторонние корни?».
- Вопросы, подводящие от частного к общему.
Например «Что общего у конуса, цилиндра, шара?».
- Вопросы, подводящие от общего к частному.
Например «Как вывести из теоремы косинусов теорему Пифагора?».
- Вопросы, требующие установления справедливости обратного утверждения или доказать, что его нет.
Например «Ромб — это параллелограмм, а параллелограмм — это ромб?».
Рассмотрим несколько задач, способствующих усилению развивающих функций у школьных задач.
- Основанием пирамиды является прямоугольник со сторонами 5 см и 9 см. Высота пирамиды проходит через точку пересечения диагоналей прямоугольника и равна 6 см. Найти боковую поверхность пирамиды.
Сложность задачи уже состоит в том, что нет понятия правильной пирамиды. И тогда обучающимся предстоит ответить на следующие вопросы:
- В чём сходство и различие между правильной и неправильной пирамидой?
- При каких условиях пирамида правильная?
- Высота пирамиды проходит через центр основания, будет пирамида правильной?
Здесь мы будем наблюдать сопоставление понятий, установление связей, умение обобщать, делать выводы. Такие вопросы будут способствовать усилению развивающей функции задачи.
Рассмотрим ещё одну задачу.
- Две вершины треугольника принадлежат плоскости. Будет ли принадлежать третья вершина, если этой же плоскости будет принадлежать центр окружности, вписанной в треугольник?
Здесь уместно задать вопросы: Какие бывают треугольники по виду? В любой треугольник можно вписать окружность? А если окружность будет описанной?
Как только мы изменим вопрос задачи обучающиеся не увидят принципиальной разницы. И дадут один и тот же ответ. Но это не правильно. Если третья вершина треугольника всегда принадлежит плоскости данной для произвольного треугольника остроугольного или тупоугольного, то для прямоугольного треугольника с центром вписанной окружности на середине гипотенузы третья вершина треугольника не всегда будет принадлежать данной плоскости.
- Стороны основания тетраэдра равны 5 см,12 см и 7 см. Все боковые ребра наклонены к плоскости основания под углом 45 градусов. Найти объем тетраэдра.
Обычно обучающиеся записывают формулу объема пирамиды и подставив данные вычисляют. Но можно найти объем более рациональным путем.
V=



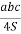
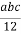
Эффективней реализовать развивающие функции задачи помогает рассмотрению ее частных и предельных случаев, поскольку это заставляет обучающихся всесторонне анализировать задачу с целью нахождения всех неё возможных решений.
- В пионерский лагерь приехали три друга: Миша, Володя и Петя. Известно, что каждый из них имеет одну из фамилий: Иванов, Семенов, Герасимов. Миша и Герасимов, отец Володи инженер. Володя учится в 6-м классе. Герасимов учится в 5-м классе. Отец Иванова слесарь. Какая фамилия у каждого из ребят?
Приведём рассуждение решения задачи.
Миша не Герасимов, значит он либо Иванов, либо Семенов. Отец Володи инженер и он учится в 6 кл., а т. к. Герасимов учится в 5 кл., то это не Володя.
Если Миша не Герасимов и Володя не Герасимов, то это Петя — Герасимов. Остается Иванов и Семенов.
Если отец Иванова слесарь, значит Миша-это Иванов, т. к. отец Володи — инженер. Остается Семенов и Володя, значит Володя Семенов [2].
Вывод: Развивать мыслительную функцию возможно при продуманной реализации всех дидактических математических задач.
Литература:
- https://moluch.ru/archive/45/5505/
- https://znanija.com/task/973063

