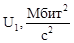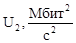В данной статье предлагается новый критерий оценки оптимальности локальной вычислительной сети по степени загруженности её участков.
Одна из важнейших характеристик сети – её загруженность. Загруженность сети определяется нагрузкой на её участки и схемой соединения сети. В настоящее время большинство компьютерных сетей строится по топологии иерархической звезды. Поэтому в данной статье нами будет рассмотрена именно эта схема соединения компонентов сети.
Оптимально бы было соединить компьютеры в один коммутатор по схеме «звезда», но во многих случаях это невозможно. Прежде всего, потому, что количество портов коммутаторов ограничено производителем. Поэтому зачастую необходимо включать в сеть несколько коммутаторов, особенно если сеть достаточно велика.
Очень часто сеть строится «по наитию», то есть включается определённое число коммутаторов, через которые подсоединяются оконечные устройства так, чтобы все оконечные устройства работали более-менее хорошо.
В данной статье нами предложен новый критерий оптимальности схемы сети, который учитывает распределение нагрузок на её участках.
Возьмём, например, пять компьютеров, которые необходимо соединить в сеть. Предположим, что мы имеем коммутаторы, к которым можно подключать не более трёх узлов (на три гнезда). Других коммутаторов у нас нет. Пусть нам также известен трафик между каждой парой компьютеров.
Обозначим трафик между парой компьютеров pij, где i,j – номера компьютеров (i<j), между которыми устанавливается соединение.
Идеально было бы подключить компьютеры в сеть так, как показано на рисунке 1.
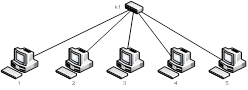
Рисунок 1 – Оптимальная схема подключения 5 компьютеров в сеть.
Но в нашем случае коммутаторы рассчитаны только на три гнезда, поэтому такое подключение невозможно. Две из возможных схем подключения компьютеров в сеть показаны на рисунке 2.
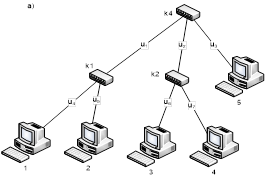
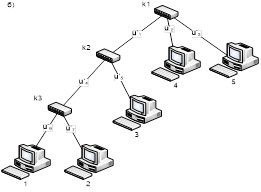
Рисунок 2 – Возможные способы подключения 5 компьютеров в сеть в случае, если коммутаторы имеют не более трёх гнёзд
Отвлечёмся пока от стоимости коммутаторов и зададимся следующей целью – определить какая именно из схем будет более целесообразна с точки зрения загрузки сети? Определим нагрузки на участках сети.
В случае а): обозначим нагрузки на участках сети через 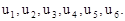
Через первый участок проходит трафик от компьютера 1 к компьютерам 3, 4 и 5 и от компьютера 2 к компьютерам 3, 4 и 5, следовательно, трафик
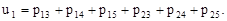 (1)
(1)
Аналогично
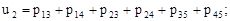 (2)
(2) 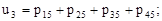 (3)
(3)
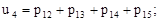 (4)
(4) 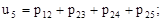 (5)
(5)
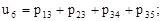 (6)
(6) 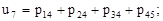 (7)
(7)
В случае б): обозначим нагрузки на участках сети через 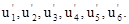
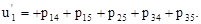 8)
8) 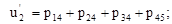 (9)
(9)
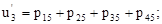 (10)
(10) 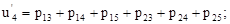 (11)
(11)
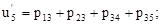 (12)
(12) 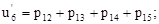 (13)
(13)
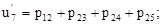 (14)
(14)
Зададимся целью: определить такую схему сети, в которой распределение нагрузок должно быть наиболее равномерным при соблюдении правила – трафики между каждой парой компьютеров должны соответствовать заданным.
Для решения поставленной задачи определим следующий критерий выбора схемы сети. Будем выбирать ту схему, для которой сумма квадратов нагрузок на каждом участке сети наименьшая, так как при решении задач минимизации отклонения экспериментальной точки от заданной кривой наилучшим образом подходит метод наименьших квадратов, допускающий довольно веское теоретическое обоснование с вероятностной точки зрения [1, 354]. При этом, очевидно, наиболее минимизируются загрузки на конкретных участках.
Таким образом, за показатель выбора того или иного соединения берём следующий критерий:
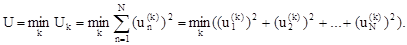 (15)
(15)
Здесь k – количество схем соединений, n – номер участка сети, 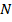 N – количество участков сети.
N – количество участков сети.
В нашем примере мы имеем два соединения (из общего количества случаев).
В случае а) (см. рисунок 2):
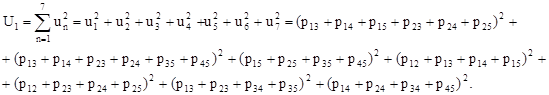
В случае б) (см. рисунок 2):
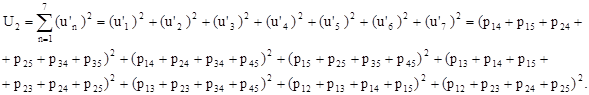
Для того чтобы выяснить, какая из величин 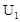 или
или 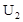 меньше, найдём их разность:
меньше, найдём их разность:
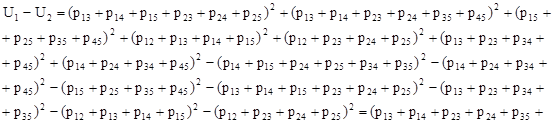
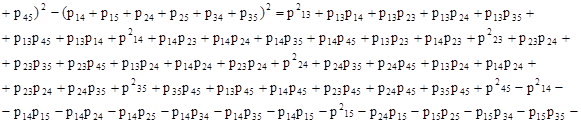
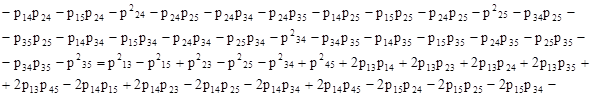

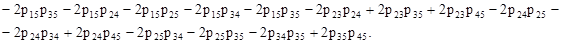
Как видим, найти знак разности, не зная нагрузок, не представляется возможным. Выполним подбор загрузки сети между компьютерами для нашего примера с помощью генератора случайных чисел в редакторе Microsoft Excel, рассчитаем загрузку участков сети и значения критериев  и
и 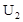 для каждого случая. Составим таблицу трафиков pij:
для каждого случая. Составим таблицу трафиков pij:
|
pij, Мб/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
|
|
|
|
|
2 |
29 |
0 |
|
|
|
|
3 |
17 |
22 |
0 |
|
|
|
4 |
35 |
19 |
35 |
0 |
|
|
5 |
14 |
27 |
34 |
17 |
0 |
Таблица 1 - Первое измерение трафики pij
По формулам (1)-(7) вычислим нагрузки на участках сети для случая а) (см. рисунок 2) (Мбит/с):
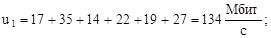
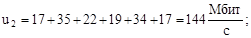
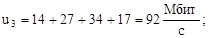
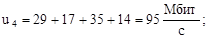
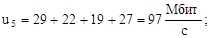
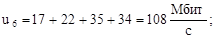
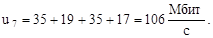
По формулам (2.8)-(2.14) вычислим нагрузки на участках сети для случая б) (см. рисунок 2.2) (Мбит/с):
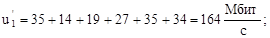
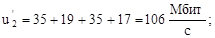
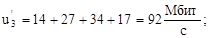
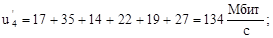
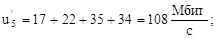
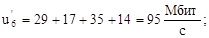
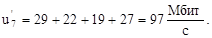
По формулам (16) и (17) вычислим величины 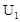 и
и 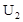 :
:
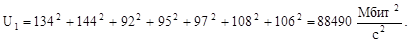
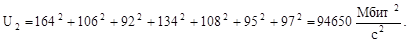
В данном случае, согласно формуле (2.15) критерий:
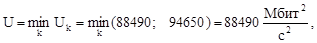
то есть, выбираем первую схему сети. Аналогично произведём расчеты ещё в 11 случаях.
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
|
|
|
|
|
2 |
13 |
0 |
|
|
|
|
3 |
36 |
39 |
0 |
|
|
|
4 |
21 |
32 |
36 |
0 |
|
|
5 |
31 |
31 |
37 |
27 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
190 |
188 |
|
2 |
192 |
116 |
|
3 |
126 |
126 |
|
4 |
101 |
190 |
|
5 |
115 |
148 |
|
6 |
148 |
101 |
|
7 |
116 |
115 |
Таблица 2 - Второе измерение
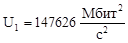
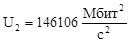
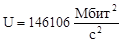
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
32 |
0 | |||
|
3 |
27 |
38 |
0 | ||
|
4 |
28 |
32 |
14 |
0 | |
|
5 |
37 |
33 |
11 |
34 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
195 |
155 |
|
2 |
170 |
108 |
|
3 |
115 |
115 |
|
4 |
124 |
195 |
|
5 |
135 |
90 |
|
6 |
90 |
124 |
|
7 |
108 |
135 |
Таблица 3 -Третье измерение
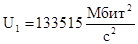
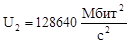
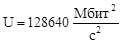
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
27 |
0 | |||
|
3 |
16 |
35 |
0 | ||
|
4 |
25 |
35 |
40 |
0 | |
|
5 |
22 |
14 |
30 |
38 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
147 |
166 |
|
2 |
179 |
138 |
|
3 |
104 |
104 |
|
4 |
90 |
147 |
|
5 |
111 |
121 |
|
6 |
121 |
90 |
|
7 |
138 |
111 |
Таблица 4 - Четвёртое измерение
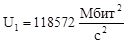
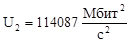
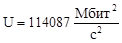
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
34 |
0 | |||
|
3 |
23 |
35 |
0 | ||
|
4 |
19 |
35 |
16 |
0 | |
|
5 |
35 |
32 |
40 |
34 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
179 |
177 |
|
2 |
186 |
104 |
|
3 |
141 |
141 |
|
4 |
111 |
179 |
|
5 |
136 |
114 |
|
6 |
114 |
111 |
|
7 |
104 |
136 |
Таблица 5 - Пятое измерение
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
190 |
151 |
|
2 |
199 |
104 |
|
3 |
95 |
95 |
|
4 |
121 |
190 |
|
5 |
147 |
117 |
|
6 |
117 |
121 |
|
7 |
104 |
147 |
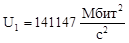
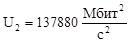
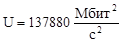
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
39 |
0 | |||
|
3 |
39 |
39 |
0 | ||
|
4 |
33 |
36 |
11 |
0 | |
|
5 |
10 |
33 |
28 |
24 |
0 |
Таблица 6 - Шестое измерение
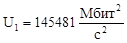
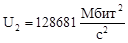
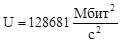
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
27 |
0 | |||
|
3 |
20 |
20 |
0 | ||
|
4 |
21 |
20 |
35 |
0 | |
|
5 |
11 |
38 |
13 |
20 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
130 |
138 |
|
2 |
114 |
96 |
|
3 |
82 |
82 |
|
4 |
79 |
130 |
|
5 |
105 |
88 |
|
6 |
88 |
79 |
|
7 |
96 |
105 |
Таблица 7 - Седьмое измерение:
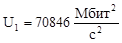
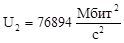
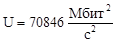
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
10 |
0 | |||
|
3 |
32 |
27 |
0 | ||
|
4 |
30 |
36 |
25 |
0 | |
|
5 |
19 |
24 |
22 |
19 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
168 |
156 |
|
2 |
166 |
110 |
|
3 |
84 |
84 |
|
4 |
91 |
168 |
|
5 |
97 |
106 |
|
6 |
106 |
91 |
|
7 |
110 |
97 |
Таблица 8 - Восьмое измерение
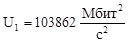
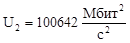
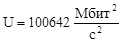
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
30 |
0 | |||
|
3 |
22 |
37 |
0 | ||
|
4 |
27 |
18 |
37 |
0 | |
|
5 |
22 |
31 |
29 |
20 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
157 |
164 |
|
2 |
153 |
102 |
|
3 |
102 |
102 |
|
4 |
101 |
157 |
|
5 |
116 |
125 |
|
6 |
125 |
101 |
|
7 |
102 |
116 |
Таблица 9 - Девятое измерение
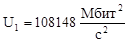
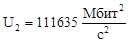
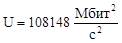
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
16 |
0 | |||
|
3 |
22 |
39 |
0 | ||
|
4 |
30 |
18 |
11 |
0 | |
|
5 |
24 |
20 |
39 |
28 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
153 |
142 |
|
2 |
176 |
87 |
|
3 |
111 |
111 |
|
4 |
92 |
153 |
|
5 |
93 |
111 |
|
6 |
111 |
92 |
|
7 |
87 |
93 |
Таблица 10 - Десятое измерение
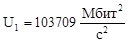
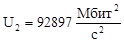
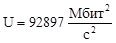
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
37 |
0 | |||
|
3 |
38 |
27 |
0 | ||
|
4 |
20 |
33 |
21 |
0 | |
|
5 |
37 |
15 |
38 |
31 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
170 |
164 |
|
2 |
187 |
105 |
|
3 |
121 |
121 |
|
4 |
132 |
170 |
|
5 |
112 |
124 |
|
6 |
124 |
132 |
|
7 |
105 |
112 |
Таблица 11 - Одиннадцатое измерение
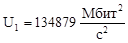
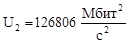
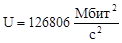
|
pij, Мбит/с |
i | ||||
|
j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0 | ||||
|
2 |
37 |
0 | |||
|
3 |
19 |
18 |
0 | ||
|
4 |
15 |
12 |
38 |
0 | |
|
5 |
37 |
30 |
10 |
37 |
0 |
|
n |
un, Мбит/с |
u'n, Мбит/с |
|
1 |
131 |
142 |
|
2 |
111 |
102 |
|
3 |
114 |
114 |
|
4 |
108 |
131 |
|
5 |
97 |
85 |
|
6 |
85 |
108 |
|
7 |
102 |
97 |
Таблица 12 - Двенадцатое измерение
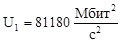
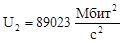
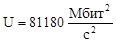
Составим таблицу критериев для случая а) и б) (см. рисунок 2) для всех измерений:
|
№ измерения |
|
|
|
1 |
88490 |
94650 |
|
2 |
147626 |
146106 |
|
3 |
133515 |
128640 |
|
4 |
118572 |
114087 |
|
5 |
141147 |
137880 |
|
6 |
145481 |
128681 |
|
7 |
70846 |
76894 |
|
8 |
103862 |
100642 |
|
9 |
108148 |
111635 |
|
10 |
103709 |
92897 |
|
11 |
134879 |
126806 |
|
12 |
81180 |
89023 |
Таблица 13 - Таблица критериев для случая а) и б)
На рисунке 3 видно, что при различных измерениях выбор схемы сети различен.
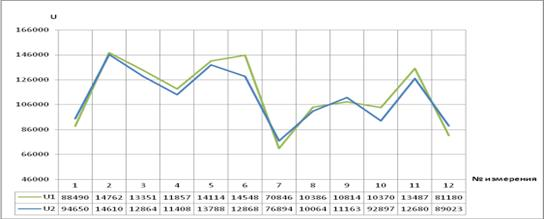
Рисунок 3 – Зависимость критерия 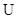 от номера измерения.
от номера измерения.
Таким образом, мы не можем точно сказать, какая из схем сети является оптимальной, не имея данных о трафике между оконечными устройствами. Имея же подобные сведения, мы легко можем определить преимущество той или иной схемы.
В расчёте для простоты мы взяли всего пять компьютеров и один вид коммутаторов. Сеть может состоять из значительного числа компьютеров, коммутаторов же выпускается тоже довольно большое количество, поэтому ручной расчёт (и даже расчёт с помощью существующих программных средств) является затруднительным.
Как решение этой проблемы автором разработана программа для выбора оптимальной схемы сети, которая будет учитывать не только её загрузку, но и стоимость оборудования.
СПИСОК ЛИТЕРАТУРЫ
1. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1969. – 576 с.