В статье рассматриваются математические основы и программная реализация генератора псевдослучайных последовательностей.
Ключевые слова: криптография, псевдослучайная последовательность, линейный конгруэнтный метод, безопасность компьютерных сетей.
Криптография — это наука, изучающая методы сохранения данных в безопасности, используя так называемые криптографические алгоритмы. Криптографический алгоритм представляет собой математическую функцию, используемую для шифрования и дешифрования. Генератор псевдослучайных чисел (ГПСЧ) — алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению. Последовательность называется криптографически надежной псевдослучайной последовательностью (КНПСП), если она непредсказуема, т. е. вычислительно неосуществимо предсказать следующий бит, имея полное знание алгоритма (или аппаратуры) и всех предшествующих битов потока. Настоящая работа посвящена в первую очередь обзору генерации псевдослучайных последовательностей, ориентированных на использование в системах защиты информации от случайных и умышленных деструктивных воздействий.
Анализ требований к программному обеспечению. В информатике самая общая методика для того, чтобы производить псевдослучайные числа — линейный конгруэнтный метод. Выбирается 5 чисел:
– Модуль n (n>0);
– Множитель a (0<=a
– Приращение b (0<=b
– Начальное значение X
0
(0<= X
0
– Количество случайных элементов в последовательности m.
Последовательность получается с использование следующей рекуррентной формулы: X
n+1
=(a
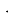
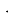
Очевидно, что эта последовательность не совсем подходит под определение случайной. Тем не менее, этот провал позволил нам сделать два важных выводов:
– Числа n,a,b, X 0 не должны быть случайными;
– Линейный конгруэнтный метод даёт нам повторяющиеся последовательности.
На самом деле любая функция, отображающая конечное множество X в X, будет давать циклически повторяемый значения. Таким образом, наша задача состоит в том, чтобы максимально удлинить уникальную часть последовательности
Анализ требований к
программному обеспечению
.
В большинстве языков программирования именно линейный конгруэнтный метод, введенный Лехмером,
используется в стандартной функции получения случайных чисел. Рис. 1. показывает этот метод, который рекурсивно создает последовательность псевдослучайных чисел, используя линейное конгруэнтное уравнение xi+1 = (a
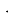
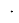
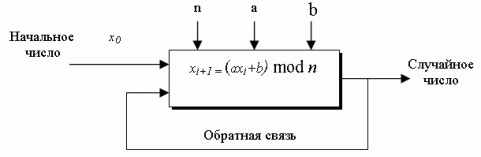
Рис. 1. Линейный конгруэнтный генератор псевдослучайных чисел
Последовательность является периодической, где период зависит от того, как тщательно выбраны коэффициенты a и b. Идеально период должен быть такого размера, как модуль n.
Инструкция пользователя. Программа генерации псевдослучайных последовательностей написана на языке программирования С#. В данной программе реализован алгоритм генерации псевдослучайных чисел, которые складываются в последовательность. Алгоритм реализован линейным конгруэнтным методом. Написанная программа в качестве входных данных запрашивает пять переменных: x 0 — первое число алгоритма на основе которой и будет происходить генерация следующих чисел; a — множитель на который будет умножаться элемент; b — элемент который прибавляется; n — делитель операции mod; m — количество элементов которое требуется сгенерировать.
Важным условием является, чтобы вводимые данные a и b являлись взаимно простыми. Это влияет на длину неповторяющейся последовательности поэтому, стоит внести в программу проверку условия взаимной простоты.
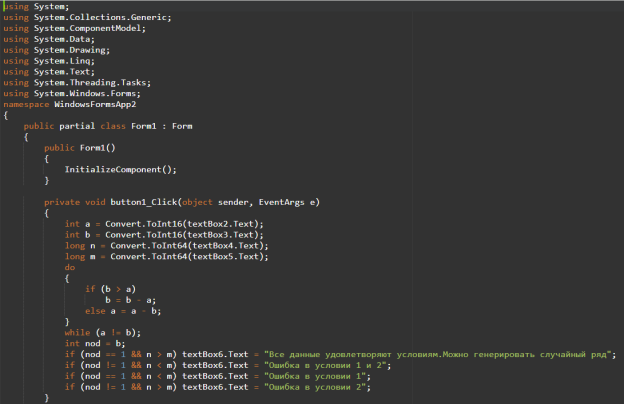
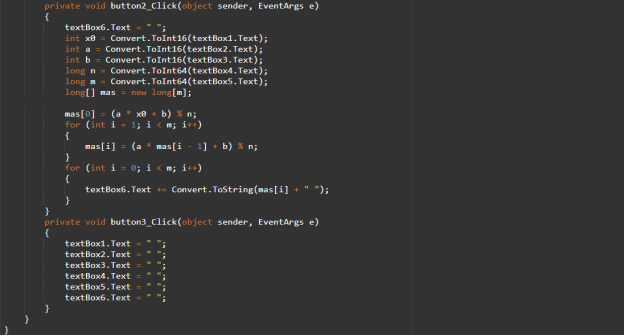
Рис. 2. Программный код
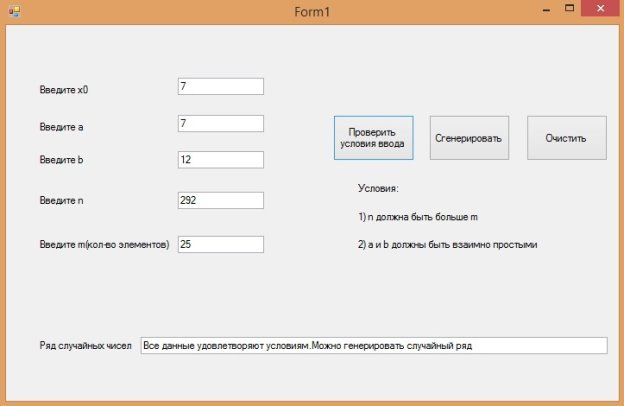
Рис. 3. Результат выполнения программы
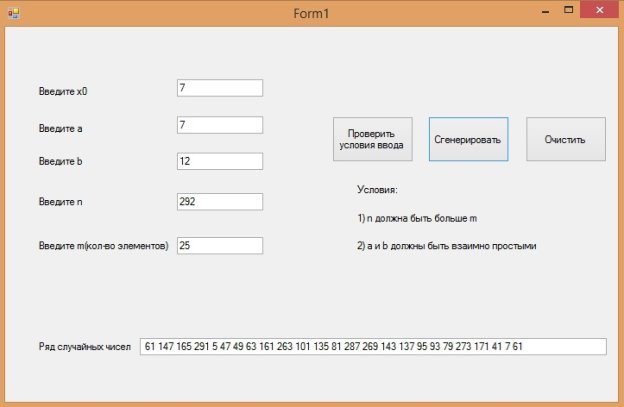
Рис. 4. Результат выполнения программы
Заключение. Современная информатика широко использует псевдослучайные числа в самых различных приложениях. При этом от качества используемых генераторов псевдослучайных чисел зависит качество получаемых результатов. Генерирование случайных последовательностей с заданным вероятностным законом и проверка их адекватности — одни из важнейших проблем современной криптологии. Генераторы случайных последовательностей используются в существующих криптосистемах для генерации ключевой информации и задания ряда параметров криптосистем. В ходе выполнения курсовой работы были изучены математические основы и программная реализация генератора псевдослучайных последовательностей (на примере линейного конгруэнтного генератора).
Литература:
- Васильева, И. Н. Криптографические методы защиты информации: учебник и практикум для академического бакалавриата / И. Н. Васильева. — Москва: Издательство Юрайт, 2019. — 349 с.
- Иванов М. А., Чугунков И. В. Криптографические методы защиты информации в компьютерных системах и сетях: Учебное пособие / Под ред. М. А. Иванова. М.: НИЯУ МИФИ, 2012. — 400 с.: ил.
- Шаньгин В. Ф. Ш20 Информационная безопасность компьютерных систем и сетей: учеб.пособие. — М.: ИД «ФОРУМ»: ИНФРА-М, 2011. — 416 с.: ил.







