В статье рассматриваются примеры из физики из различных разделов физики. Объединяющим фактором этих примеров является экспоненциальный характер математического описания физических процессов.
Ключевые слова: экспоненциальная зависимость, экспонента, число Е, скорость изменения физической величины, дифференциальное уравнение.
Одним из задач исследования прикладной математики является изучение физических процессов, в которых скорость изменения некоторой величины пропорциональна уже достигнутому значению самой этой величины .
Обозначим через y(t) значение рассматриваемой физической величины в момент времени t . Через y мы обозначим изменение величины у за малый промежуток t от t до t+t то есть
y = y(t+t)-y(t)
Скорость изменения величины
у
можно приближенно представить отношением


где k коэффициент пропорциональности. Этот коэффициент может быть как положительным числом, так и отрицательным.
При t это соотношение можно писать в таком виде:
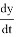
Последнее уравнение называется дифференциальным уравнением первого порядка. С ним школьники старших классов знакомы с математики. Решение этого дифференциального уравнения имеет вид
y(t) = y(0)
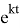
где у(0) называется начальным условием, т. е. значение величины у в момент времени t=0 , е — основание натуральных логарифмов.
Функции в зависимости от некоторых величин, содержащие число «е», называют экспонентами. Формулу (1) в большинстве случаев пишут так:
y(t) = y(0) exp kt.
Экспоненциальные зависимости в физических явлениях
Пример 1 . Катер массы m движется по озеру со скоростью 0 . В момент t=0 выключили его двигатель. Считая силу сопротивления воды движению катера пропорциональной его скорости F = -r, найти скорость катера в зависимости от времени.
Анализ: После выключения двигателя катер движется только под действием силы сопротивления воды. Поэтому уравнение движения катера в скалярном виде:
—
r = ma -r = m
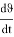
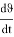

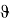
Последнее выражение называется дифференциальным уравнением первого порядка.
Значит убывание скорости катера прямо пропорционально самой скорости катера.
Дифференциальное уравнение напишем в такой форме:


Интегрируя это выражение
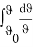
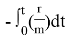
получим
ln
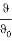

откуда
=
0

Пример 2. Найти давление воздуха в откачиваемом сосуде как функцию времени откачки t . Объем сосуда V , первоначальное давление p 0 . Процесс считать изотермическим и скорость откачки, не зависящей от давления и равной С .
Примечание: Скоростью откачки называют объем газа, откачиваемый за единицу времени, причем этот объем измеряется при давлении газа в данный момент.
Анализ: За время dt объем откачки газа равен dV=Cdt
Поскольку, процесс изотермически, напишем:
pV=const
Или
d(PV) = VdP + PdV = 0
откуда
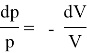
Следовательно,
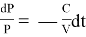
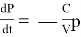
Проинтегрировав
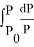

найдем уравнение давления газа в зависимости от времени:
p=p
0
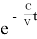
Пример 3 . Найти закон радиоактивного распада как функцию времени t. В начальный момент (t=0) мы имели N 0 атомов радиоактивных атомов. Из эксперимента известно, что среднее число атомов, распадающихся за малый промежуток времени, пропорционально количеству имеющихся атомов.
Анализ: Из условия задачи мы можем написать следующие уравнения:
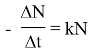
Знак минус перед скоростью распада означает, что идет убыль численности не распавшихся атомов.
Поскольку t0, последнее выражение напишем в форме дифференциального уравнения:
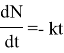
Отсюда найдем закон радиоактивного распада:
N=N
0
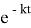
Если принимается во внимание понятие периода полураспада Т, то этот закон примет вид
N=N 0
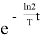
Пример 4. Известно, что при наличии разности температур между телом и окружающей средой теплоотдача тела за время t определяется формулой
Q k(T — T c )t
Q — количество отдаваемой теплоты тела к окружающей среде за время t; Т — температура тела, T c — температура окружающей среды, коэффициент k зависит от поверхности и природы тела.
Пусть тело нагрето до температуры Т 0 ; температуру окружающей среды считаем постоянной (Т с Т 0 ). Найти зависимость температуры Т тела от времени охлаждения t.
Анализ: При охлаждении тела количество отдаваемой теплоты выражается через Q=СT. Тогда мы можем написать следующее уравнение:
СT= — k(T — T c )t
или
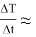
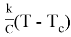
Следовательно,

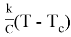
Знак минус выбран потому, что возрастанием времени t температура Т тела уменьшается.
Разделяя переменные, получим
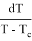
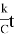
Отсюда
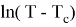

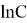
Подставляя начальное условие T t =0 =T 0 , найдем С. C = T 0 -T C .
Окончательно закон охлаждения тела в условиях постоянства температуры окружающей среды имеет вид
T=T
c
+ (T
0
-T
C
)
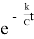
В условиях T C =0 получим
T=T
0
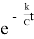
Пример 5. Установить формулу, характеризующую динамику цепной ядерной реакции в зависимости от времени, если известно следующие параметры данной реакции: скорость развития цепной реакции зависит от коэффициента k размножения нейтронов и от среднего времени между двумя последовательными актами деления. Таким образом, коэффициент пропорциональности, характеризующий скорость прироста нейтронов приблизительно равен
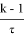
Анализ: Прирост числа нейтронов за единицу времени характеризует следующее дифференциальное уравнение:
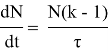
Интегрируя это уравнение, получим
N=N
0
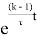
Пример 6. Доказано, что параллельный пучок лучей (или частиц), проходя через слой вещества, уменьшает свою интенсивность.
Если толщина слоя достаточно мала, то изменение интенсивности пучка пропорционально толщине слоя:
Ik 1 l
А количество поглощенных квантов (или рассеянных частиц) пропорционально интенсивности пучка:
I = — k 2 I
Коэффициенты k 1 и k 2 зависят от свойств поглощающей среды. Найти закон ослабления интенсивности излучения при прохождении через поглощающую среду.
Анализ: Объединяя обе формулы, приведенные в условии задачи, получим:
I — kIl
Отсюда:
I=I
0
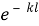
Литература:
- Осятинский С. Д., Л. З. Румшиский. Экспонента // Квант. — 1972. — № 12. с.19–25.
- Слободецкий И. Ш., Асламазов Л. Г. Задачи но физике.- М.: Наука, 1980.—(Библиотечка «Квант», вып. 5). — 198 с.







