At present, the intensive development of hydraulic engineering construction, not only in our country around the world, has caused the need to take into account the impact of various structures on channel processes, especially on flat rivers. The studies of the last period are devoted to the development of these problems, which made it possible to develop methods for calculating channel deformations during the construction of hydraulic structures of various types.
Keywords: river, river bed, soil type, sediment, flow, relief, deformation.
В настоящие время интенсивное развитие гидротехнического строительства не только в нашей стране, но и по всему миру вызвало необходимость учёта воздействия различных сооружений на русловые процессы, особенно на равнинных реках. Разработке этих проблем посвящены исследования последнего периода, позволившие разработать методы расчета русловых деформаций при возведении гидротехнических сооружении различных типов.
Ключевые слова : река, русла, тип грунта, наносы, поток, рельеф, деформация.
At present, the intensive development of hydraulic engineering construction, not only in our country around the world, has caused the need to take into account the impact of various structures on channel processes, especially on flat rivers. The research of the last period is devoted to the development of these problems, which made it possible to develop methods for calculating channel deformations during the construction of hydraulic structures of various types.
The complexity of studying the dynamics of channel flows and channel processes is associated with eroded soils.
As you know, the channel process is a complex multifactorial phenomenon, that any section of the river receives the sediment runoff specified by its natural conditions, which the flow must transport downstream. Such a flow depends on the relief, the geology of the water and ice regimes, the runoff of suspended sediments, the mode of their input, the size of the sediments and the size of the sediment inflow, their composition depends on multiple natural factors: precipitation, slopes of the drainage surface, soils and their vegetation permeability. etc. All this makes the channel process a complex multifactorial phenomenon that can be studied only on the basis of a well-grounded multifactorial approach and can give useful results.
It should be noted that solving the problem of calculating and forecasting the channel process requires the creation of a hydraulic theory and taking into account the morphological aspects of the problem.
Usually, the dynamics of channel flows and channel processes are studied in nature or in laboratory conditions based on a model of rivers (or in a part of a river).
Naturally, creating a model requires a huge amount of material costs and human time. Sometimes the smallest change in flow parameters requires reworking the experimental setup.
In such cases, the most convenient economical and effective method for studying the river channel is using mathematical modeling of this process. Which allows in a wide range of changes in the parameters of the river channel, channel, such as geometrical dimensions, relief, imbieves, sediments, etc., which does not require any changes in mathematical models, in addition, this method of research allows to predict the river channel in many ways [3].
The mathematical model of channel flows is based on the dynamics of fluids (multiphase media). The regime of water flow in rivers is, as a rule, turbulent; therefore, the dynamics of channel flows is based primarily on the laws of turbulent fluid motion.
The mathematical model of channel flows is based mainly on fundamental physical laws: conservation of matter (mass) and conservation of energy, and such movements. This paper presents the basic equations and a method for calculating the deformations of some channel deformations [1].
The main system of equations for the dynamics of channel flows contains the following components: the equation of water motion, the equation of continuity and the equation of deformations [1, 4].
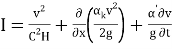
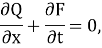
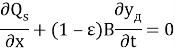
This system of equations is not closed, since it contains six unknown functions of the longitudinal coordinate (x) and time (t): y_d, H, B, v, C, and Q_s [5].
The system of equations or a mathematical model of deformation of channel rivers is unsteady, and requires the solution of the boundary and initial conditions for unknowns are determined by the specific conditions of the problem [2]. In addition, to close the system of equations, a number of relations (equations) of these relations are required. those. The connection between the unknown system can be obtained experimentally or semi-empirically.
Conclusion: The system of equations with a number of justified assumptions, initial and boundary conditions is solved for a specific problem by the finite-difference method. The results were obtained along the longitudinal direction of the river and in time.
References:
- Н. Б. Барышников, И. В. Попов. Динамика русловых потоков и русловые процессы. Ленинград гидрометеоиздат 1988. с.455.
- А. А. Самарский. Теория разности схем. -3-е изд. –М.: Наука. 1989. с.616.
- Исмагилов Х. A. Селевые потоки, русловые процессы, противоселевые и против паводковые мероприятия в Средней Азии. Ташкент, 2006. p. 262.
- Исмагилов Х. A., Ибрагимов И. A. Движение паводковых вод в руслах в условиях зарегулированного стока воды. Журнал “Проблемы механики” № 1, Ташкент, 2014. с.69–71.
- Исмагилов Х. A., Ибрагимов И. A. Рекомендации по гидравлическому расчету и креплению берегов русла р. Амударьи в условиях зарегулированного стока воды. Журнал “Проблемы механики” № 1. Ташкент, 2014. с.66–69.

