Оценка параметров полигармонических сигналов методом машинного обучения



1 Введение

Тема работы посвящена исследованию возможности применения классических методов машинного обучения к оценке параметров и прогнозированию нерегулярных колебательных процессов. Известно, что полигармоническое колебание <на глаз> бывает трудно отличить от хаотического. Однако задачи прогнозирования для полигармонического процесса решается легче, поскольку модель процесса не обладает свойствами локальной неустойчивости (<разбегания траекторий>). В статье разработаны программы оценивания параметров и прогнозирования полигармонических колебаний на основе методов решения целевых неравенств, развитых В. А. Якубовичем и его учениками [1, 2, 3, 4]. Особенностью задачи является наличие ограниченных погрешностей измерений, затрудняющих применение традиционных методов математической статистики.

2 Постановка задачи

Пусть измерению доступен сигнал вида:

y ( t ) = A ₁ sin( ω ₁ t ) + ... + A _n sin( ω _n t ) + φ ( t ) , (2.1)

где n ≥ 2, ω _i и A _i — неизвестные частоты и амплитуды, φ ( t ) — ограниченная помеха: |φ ( t ) | (; ∆ _φ < ∞ . Отслеживать можем только суммарный сигнал y , про отдельные составляющие неизвестно.

Задача состоит в том, чтобы оценить неизвестные частоты ω _i и амплитуды A _i ( i = 1 ,..., n ) и построить модель y ˆ( t ) сигнала y ( t ) с заданной точностью.

Модель строится с оценочными коэффициентами и выглядит:

y ˆ( t ) = A ^ˆ 1 sin( ω ˆ ₁ t ) + ... + A ˆ n sin( ω ˆ _n t ) . (2.2)

Для дискретных точек t _i = i · h с шагом h = 1 / 100, i = 1 ,..., N , где N — количество точек, вводим цель оценивания:

|y _i − y ˆ _i | 2 < δ, i = 1 ,..., N, (2.3)

где δ — заданная точность, y _i = y ( t _i ) и y ˆ _i = y ˆ( t _i ) .

Сигнал (2.1) двукратным дифференцированием можно свести к уравнению y ¨ + ω ² y = 0, которое удобно для оценки неизвестного параметра ω ² .

По аналогии для разных n будет получаться система из n таких же дифференциальных уравнений. Выражения с суммой и произведением неизвестных параметров в них будут переобозначаться в θ _i и решение будет состоять в получении оценочных θ ^ˆ i с заданной точностью.

3 Оценка параметров алгоритмом «Полоска» в условиях помех

Для поставленной задачи существует несколько решений через методы: рекуррентных целевых неравенств (РЦН), стохастической аппроксимации, многошаговых алгоритмов адаптации. Мы хотим исследовать возможность аппроксимации полигармонических сигналов с помощью конечно-сходящегося алгоритма, рассчитывая, что при большом числе параметров он будет проще и иметь меньшую чувствительность к помехам.

Для описания алгоритма «Полоска» [4, 5, 6] в условиях нашей задачи рассмотрим модель (2.1) в общем виде:

y = θ ^T x + φ,

где y — выходная переменная, θ и x — векторы параметров и входов системы, они подробно описаны в пунктах с оценкой параметров, |φ ( t ) | (; ∆ _φ .

Задача сводится к решению рекуррентных целевых неравенств относительно вектора неизвестных параметров θ .

|y _k − θ ^T x _{k − 1} | (; C, k > k ^∗ < N. (3.1)

Здесь k — номера шагов при решении неравенств, а y _k — входящий сигнал с помехой, полученный по дискретному аналогу формулы (2.1), а C — константа, характеризующая ширину полосы.

Тогда алгоритм «Полоска» [4, 5, 6] строится следующим образом:

(3. 2)

Здесь η _k = y _k −θ ^T x _{k − 1} , x _k , ρ ∈ (0; 1) — постоянный параметр и µ ∈ (0; 2(1 − ∆ φ )1 — произвольный параметр алгоритма.

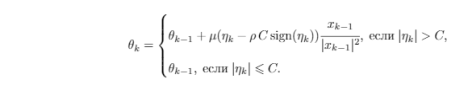
Свойства подобных и более общих алгоритмов впервые были изучены в рамках развитого В. А. Якубовичем и его учениками метода решения рекуррентных целевых неравенств [1, 2, 3].

Было доказано в [1, 2, 4, 5, 6], что различные модификации алгоритма «Полоска» сходятся за конечное число шагов. В постановке нашей задачи к входному сигналу добавили ограниченное возмущение φ ( t ), поэтому нужно получить условия сходимости алгоритма в этом случае. Они даются следующей теоремой.

Теорема 1. Если существует такой вектор θ ^∗ , что

|y _k − θ ^∗ x _k | <= C ∀k,

где y _k — полученный из формулы (2.1) входящий сигнал, в котором помеха |φ ( t _k ) |<=c· ∆ _φ , то алгоритм

(3.2) — конечно сходящийся, т. е. θ _k = θ _{k − 1} и |η _k | (; Cпри всех достаточно больших k.

Доказательство основано на применении и расширении результата известной теоремы из книги В. А. Якубовича на случай наличия помех. Верхняя оценка помехи здесь больше той, которая в постановке задачи. Это связано с определенным оцениванием сигнала по дискретной формуле.

Таким образом, при рассмотрении неравенств не важно, есть ограниченная помеха или нет. Нам важно, какое неравенство разрешимо и при какой ширине полосы.

4. Оценка параметров алгоритмом «Полоска» в условиях помех

Подробно рассмотрим метод на частном случае нашей задачи, он будет применяться и для больших n . Решение задачи основано на оценке модели сигнала в виде дифференциального уравнения порядка 2 n .

Бигармоническая модель выглядит так:

y ( t ) = A ₁ sin( ω ₁ t ) + A ₂ sin( ω ₂ t ) + φ ( t ) . (4.1) Разделив сигнал (4.1) на сумму двух составляющих, модель (4.1) можно свести к системе дифференциальных уравнений, дискретизировать уравнения вида <вход-выход> и получить расчетную модель. Применением формулы Тейлора получены оценки погрешности дискретизации.

3.1 Оценка параметров для n = 2

Применяем алгоритм для n = 2 с ω ₁ = √ 2, ω ₂ = 2, значит θ ₁ = 6, θ ₂ = 8. Помеха φ = 10 ^{− 5} sin(50 ·k·h ). Зададим число точек N = 1000, h = 1 / 100, C = 10 ^{− 8} , φ = 10 ^{− 5} sin(50 · k · h ), µ = 0 . 0503, ρ = 0 . 6. Параметры µ и ρ подбираются для каждого случая задачи.

а) φ = 10 ^{− 5} sin(50 · k · h ).б) φ = 0.

Рис. 1. Сравнение графиков y _k (синим) и y ˆ _k (красным) для n = 2, ω ₁ = √ 2, ω ₂ = 2

Получим сходимость за 86 шагов и оценки θ ^ˆ 1 = 6 . 0510, θ ^ˆ 2 = 8 . 0755 и пересчитаем их в исходные.

Получаем решение ω ˆ ₁ = 1 . 4097, ω ˆ ₂ = 2 . 0159. Получившаяся погрешность менее одного процента.

Построим график с выбранными параметрами и приближенными на Рис. 1 для случая с помехой и без. Было подсчитано, что при изменении параметров θ ^ˆ по ходу алгоритма значение функционала

Q ( θ ) уменьшается.

5. Сравнение с МНК

Проведем сравнение алгоритма «Полоска» и метода наименьших квадратов (МНК) для оценки параметров сигнала с помехой.

Как говорилось ранее, в случае наличия возмущений в сигнале он может не работать или давать большую погрешность. Проверим это, проведя оценки для смоделированного сигнала с помехой и без нее.

Зададим функцию по формуле yk = sin(ω1 · k · h) + sin(ω2 · k · h) + φ(k · h) с помехой. Зададим число точек N = 1000, h = 1/100. Начальное приближение вектора параметров — θˆ1 = 1, θˆ2 = 1.

а) МНК.б) «Полоска»

Рис. 3. Сравнение графиков y _k и y ˆ _k МНК и «Полоски» для n = 2, ω ₁ = √ 2, ω ₂ = 2, φ = 10 ^{− 5} sin(50 ·k·h )

а) МНК.б) «Полоска».

Рис. 4: Сравнение графиков y _k и y ˆ _k МНК и «Полоски» для n = 3, ω ₁ = √ 2, ω ₂ = √ 3, ω ₃ = 2, φ = 10 ^{− 9} sin(50 · k · h )

Известно, что МНК дает хорошую точность с помехами статистического характера. В нашей задаче помехи имеют хаотический характер, что не подходит для МНК. Поэтому приближение МНК получается хуже, чем алгоритмом «Полоска».

6. Заключение

Для решения задачи определения неизвестных параметров с заданной точностью в полигармоническом сигнале с ограниченной помехой был применен метод рекуррентных целевых неравенств, а точнее, алгоритм «Полоска». Выбранный нами алгоритм показал высокую точность определения параметров, и оценочная модель сигнала имела отклонение менее 1 процента. Дальнейшее исследование может быть посвящено оценке параметров сигнала при неизвестном n .

Литература:

1. Якубович В. А. (1966) Рекуррентные конечно сходящиеся алгоритмы решения систем неравенств // Докл. АН СССР. Т166. № 6. С. 1308–1311.
2. Якубович В. А. (1969) Конечно сходящиеся алгоритмы решения счетных систем неравенств и их применение в задачах синтеза адаптивных систем // Докл. АН СССР. Т189. № 3. С. 495–498.
3. Фомин В. Н. (1976) Математическая теория обучаемых опознающих систем. Л.: Изд-во ЛГУ.
4. Фомин В. Н., Фрадков А. Л., Якубович В. А. (1981) Адаптивное управление динамическими объектами. М.: Наука.
5. Фрадков А. Л. (1990) Адаптивное управление в сложных системах. М.: Наука.
6. Андриевский Б. Р., Фрадков А. Л. (2001) Элементы математического моделирования в программных средах MATLAB 5 и Scilab. СПб.: Наука.