В статье авторы приводят исследование различных алгоритмов машинного обучения для дальнейшего применения в задаче прогнозирования потребления энергии здания.
Ключевые слова: машинное обучение, прогнозирование.
Ежегодно множество компаний закупает ресурсы для собственных нужд в процессе эксплуатации из единой энергосистемы. Закупка электроэнергии осуществляется на основании прогнозирования. Поэтому необходимо как можно точнее определить величину объема закупаемых ресурсов для внесения соответствующей оплаты.
Целью данной работы является исследование различных алгоритмов машинного обучения для дальнейшего применения в задаче прогнозирования потребления энергии здания.
Задача, рассматриваемая в данной работе: ASHRAE — Great Energy Predictor III, взята с платформы для проведения конкурсов по машинному обучению Kaggle [1]. Требуется предсказать потребление энергии для здания с учетом известных метеорологических данных. Даны значения потребления энергии для здания в течение года, а также данные по погоде. Задача предполагает использование регрессионных алгоритмов машинного обучения.
Поскольку в наборе данных имеются столбцы с пропущенными значениями, возникает необходимость перейти к данным, не имеющим пропусков, с целью дальнейшего применения алгоритмов машинного обучения. Для решения этой проблемы воспользуемся методами заполнения пропусков. Т. к. пропуски в данных имеются лишь в столбцах с количественными переменными, заменим их на среднее арифметическое значение по столбцу (воспользуемся функцией “mean” [2]).
В качестве инструмента решения задачи будет использован высокоуровневый язык программирования общего назначения Python [3]. Данную задачу будем решать, применяя вид машинного обучения «с учителем» (при таком обучении делаются выводы о тестовых данных на основе данных обучения). Для начала выбранные модели необходимо обучить, а затем протестировать на выборках, являющимися частями исходного набора данных. Обучающая выборка содержит в себе 80 %, а тестовая — оставшиеся 20 % исходного набора данных.
Воспользуемся методами, основанными на регрессии. В некоторых случаях алгоритм линейной регрессии может стать нестабильным, из-за чего может возникнуть проблема переобучения. Переобучение — ситуация, когда модель корректно решает задачу на тренировочной выборке, но дает плохие результаты на тестовых. Решить данную проблему можно наложением ограничений на регрессионную модель, то есть применением регуляризации.
Для построения воспользуемся следующими алгоритмами машинного обучения:
- Linear Regression [4]
- LASSO Regression [5]
- Bayesian Ridge Regression [6]
Затем при помощи функций из библиотеки Scikit-learn [7] строим модели, основанные на вышеизложенных алгоритмах. Результаты построенных моделей по условию задачи оценивались при помощи Root Mean Squared Logarithmic Error (RMSLE) [8]:
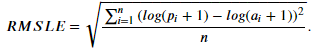
Чем эта ошибка меньше, тем лучше выбранная модель решает задачу.
После построения и оценки моделей с использованием метрики, описанной выше, получаем результаты, представленные на Рисунке 1 и занесенные в Таблицу 1:
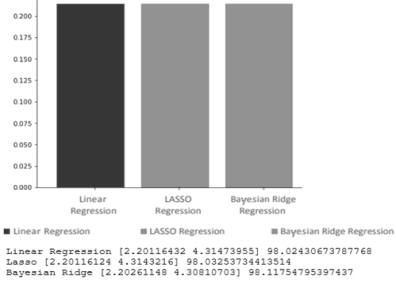
Рис. 1. Результаты примененных алгоритмов
Таблица 1
Результаты примененных алгоритмов
|
Алгоритм |
RMSLE |
|
Linear Regression |
0.2141227114423071 |
|
Lasso Regression |
0.21411934078081465 |
|
Bayesian Regression |
0.21407602876767776 |
Коэффициенты алгоритмов Linear Regression, LASSO и Bayesian Ridge практически идентичны, качество выбранных методов также почти не отличается, следовательно, использование каких-то других методов помимо обычной линейной регрессии нецелесообразно, т. к. это не даст нам никакого особого выигрыша в данной задаче.
Литература:
1. ASHRAE — Great Energy Predictor III // Kaggle URL: https://www.kaggle.com/c/ashrae-energy-prediction (дата обращения: 15.02.2021).
2. Mathematical statistics functions URL: https://docs.python.org/3/library/statistics.html (дата обращения: 16.02.2021).
3. Python 3.8.0 documentation / Python 3.8.0 documentation URL: https://docs.python.org/3/ (дата обращения: 15.02.2021).
4. Linear Regression URL: http://www.stat.yale.edu/Courses/1997–98/101/linreg.htm (дата обращения: 22.02.2021).
5. A Complete understanding of LASSO Regression URL: https://www.mygreatlearning.com/blog/understanding-of-lasso-regression/ (дата обращения: 15.02.2021).
6. Bayesian linear regression URL: https://en.wikipedia.org/wiki/Bayesian_linear_regression (дата обращения: 16.02.2021).
7. Открытая библиотека машинного обучения scikit-learn. URL: https://scikit-learn.org/ (дата обращения: 16.03.2021).
8. Understanding Root Mean Squared Logarithmic Error (RMSLE) URL: https://www.kaggle.com/carlolepelaars/understanding-the-metric-rmsle (дата обращения: 16.02.2021).







