Исследование прочности морского льда с применением теории о трещиностойкости



В статье автор описывает возможность применения балочной теории о трещиностойкости в расчете прочности льда.

Ключевые слова: морской лед, испытание на сжатие, керны, модели.

Морской лед никогда не замерзает до конца. Всегда есть кармашки рассола и газовые пузыри, которые вносят специфику в его механическое поведение. Для испытаний на сжатие используются керны, которые достаются из льда методом бурения. Традиционная форма таких образцов цилиндрическая. Керн обтачивается с двух сторон, устанавливается между двумя траверсами испытательной машины и сжимается. Для определения прочности на сжатие можно прибегнуть к балочной теории. Согласно данной теории, используется критерий роста трещины Гриффитса, который говорит о том, что упругая энергия может быть использована для роста трещины. Применительно ко льду можно говорить, что мы получили вторую ветку для малых зерен, которая была экспериментаторами выделена.

Согласно исследованиям [2, 6, 12, 13, 20], предел прочности льда при изгибе зависит от скорости действия прилагаемой нагрузки, размера образцов, их структуры, солености, плотности и температуры. Наиболее прочным при изгибе является пресный и распресненный лед [1]. Самыми прочными являются прозрачные образцы льда в верхней и средней частях льдины, где средние значения σ _изг составляют около 1,3 МПа, а максимальные значения достигают 1,88–2,17 Мпа [2]. Наименее прочным оказывается матовый лед зернистой структуры, разрушающийся при нагрузке до 1,5 МПа в поверхностном слое, около 1,0 МПа — в среднем и до 1,0 МПа — в нижнем [3].

Диапазон изменений предела прочности при изгибе, как показывают исследования льдов северного Каспия, значителен — от 0,01 до 2,17 Мпа [4].

Методы исследования

При сжатии лед демонстрирует различные сценарии разрушения: сдвиг (shear fault) и расщепление (splitting). При плоском сдвиге (рисунок 1а) возникают наклонные плоскости разрушения (прочерченные фломастером). Расщепление (рисунок 1б) характеризуется выкалыванием вертикальных «щепов» в стороны, из-за большого количества макротрещин [5].

Как показано на графике (рисунок 2), в зависимости от скорости деформирования различаются режимы вязкого разрушения и хрупкого разрушения [6]. На оси абсцисс Ох вертикальной чертой показа граница, разделяющая эти два режима разрушения морского льда . Условно эта величина принята равной .

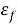
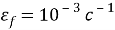
а)б)

Рис. 1. Сценарии разрушения морского льда: а) сдвиг (shear fault); б) расщепление (splitting)

Показанные выше сценарии разрушения образцов, оба, оказывается, будут соответствовать вязкому разрушению. несмотря на то, что результаты двух экспериментов различаются [7, 8]. Это связано с тем, что при разрушении образец продолжает нести нагрузку. И довольно долго. Даже для такого классического случая цилиндра лед может демонстрировать различные сценарии поведения [9].

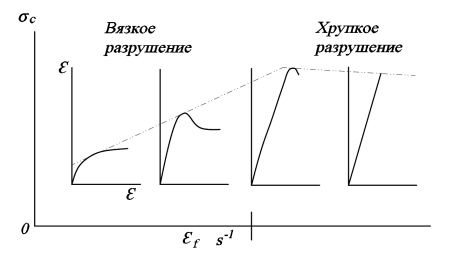
Рис. 2. Режимы вязкого и хрупкого разрушения

Лед очень удобный материал. Будучи в тонких срезах на пульверизаторе, четко выделяется структура. Можно посчитать форму зерен, которые, в отличии от металла, большие: для озерного льда эти размеры могут достегать 10 см, а для морского льда размер колеблется от долей миллиметра и до 5 мм. На графике (рисунок 3) показаны два режима (I и II) разрушения льда, применительно к графику прочности [10, 13].

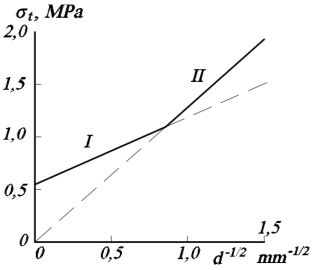
Рис. 3. Режимы разрушения льда, в зависимости от диаметра зерен

Обратный корень из диаметра зерна показывает, что более крупные зерна будут лежать ближе к нулю, а более мелкие зерна, наоборот, буду лежать в области за единицу. Видно, что первый участок зависимости прочности от зерен характеризуется плотностью зарождения дефектов. Это хорошо описывается законом Холла-Петча [11]. А второй, для более мелких зерен, определяется ростом трещин [12]

Результаты и анализ

Классическим определением коэффициента К ₁ являет бразильский тест, придуманный бразильским инженером Карнейром [14]. Тест позитивен в двух аспектах: простота получение образца и то, что вдоль линии действия сжимающих нагрузок действуют равномерные растягивающие напряжения. Отличительная особенность упругости: не смотря на криволинейную геометрию образца, поле напряжений растягивающих равномерно.

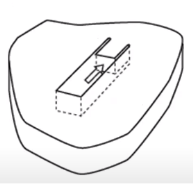
Был проведен натурный эксперимент. В толстой льдине выпиливается прямоугольная майна, куда опускается силовая ячейка. Под действием сили тяжести плита рабочей частью начинает давить короткий столбик (рисунок 4а). На рисунке 4б стрелкой показано направление нагрузки [15].

а)б)

Рис. 4. Испытания льда на сжатие: а) результат сжатия образца, б) схематические движение индентора

В верхнем слое видны пластинки толщиной 8–10 сантиметров. Это обусловлено тем, что плита разделилась на 3 «дощечки» двумя параллельными линиями (splitting). Под действием нагрузки произошло расщепление, разделение образца на части вдоль действия нагрузки.

Для описания данного явления можно воспользоваться математическими и физическими моделями. Она из таких моделей была придумана Кендаллом [16].

Использовалась она в основном для хрупких материалов, наподобие керамики, а не для льда. Модель используется для определения трещиностойкости (рисунок 5).

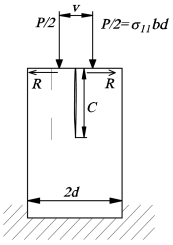
Рис. 5. Нагружение образца и образование трещины

В пластинке выполняется разрез длины С, м, так, чтобы в кончике трещины был минимальный радиус закругления. У образца получается два плеча, которые нагружаются внецентренно. Используется балочная теория (рисунок 6), от балки кое-то есть w(0)=w(c)=w’(c)=0.

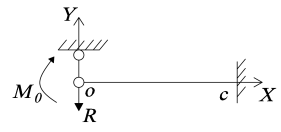
Рис. 6. Схема связей

,(1)

,(2)

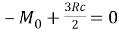
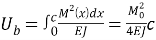
где .

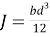
Перейдем к балочной модели. Поскольку видно, что нагрузка расположена от нейтральной оси обоих плеч ближе к надрезу, то возникающий момент приводит к тому, что плечи наклоняются друг к другу, и возникает реактивная сила R, кН. Прогиб на концах равен нулю. Из этого условия находится связь между реактивной силой R, кН, и моментом М ₀ , кН*м. Это есть следствие решения задачи изгиба. Дальше определяется упругая энергия изгиба для балки. После используется критерий роста трещины Гриффитса, который говорит о том, что упругая энергия может быть использована для роста трещины. Критерий роста трещины [18]:

,(4)

,(5)

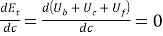
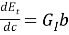
где

.

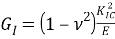
Условия , кН*м, связано с параметрами материала и геометрией (формула 6):

.(6)

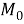
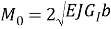
Отсюда можно найти критическую нагрузку , кН (формула 7):

(7)

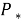
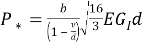
В рамках балочной модели критическая нагрузка не зависит от длины разреза. Поэтому Кенделлом был придуман этот образец, так как он обеспечивается устойчивый и управляемый рост трещины в условиях сжатия. За счет этого можно определять не только в конкретной точке, но и в процессе нагружения и продвижения трещины вдоль образца []18.

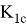
Теперь применительно ко льду. Все формулы выражены через . Все это получено простым подставленным параметров балки. И выражением Ирвина для :

,(8)

,(9)

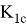
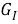
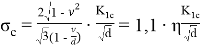
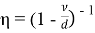
Для льда (Sanderson): .

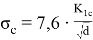
Мы видим, что которая есть осредненная по площади сечения критическая нагрузка

оказывается равняется деленная на , где характерный размер этой балки [19]. Применительно ко льду можно говорить, что мы получили вторую ветку для малых зерен, которая была экспериментаторами выделена. А вот параметрами безразмерной , которая характеризует эксцентриситет приложения нагрузки для льда, я так думаю, он характеризует неоднородность напряженного состояния в образце при сжатии, вызванное как неоднородностью упругих свойств зерен, так и наличием дефектов: газовые пузырики, кармашек рассола. Чем нравится этот подход и формула, он приводит к осмысленному результату с помощью минимальных аналитических затрат [20].

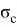
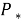
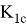
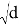
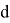
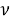
Возникает вопрос: правильно или нет использовать балочный подход.

Вот тут экспериментальная проверка (рисунок 7). Видны вверху три образца, находящиеся в испытательной машине. Первый образец, за счет изгиба появился просвет. Второй образец — видно из кончика надреза первоначального начинает распространяться трещина вдоль линии действия силы. Третий интересен тем, что надрез существует, от верхнего торца отходит еще одна трещина. Сплиттинг идет несмотря на подготовленный дефект, лед предпочел разрушаться по собственному сценарию [20].

Рис. 7. Экспериментальное сжатие ледяных кернов

Дефранко — формулы по балочной теории — соответствует коэффициенту К1с 0,9 МПа на корень из метра (рисунок 8). Это вот то значение, К1с, которое стабильно замерялось для морского льда.

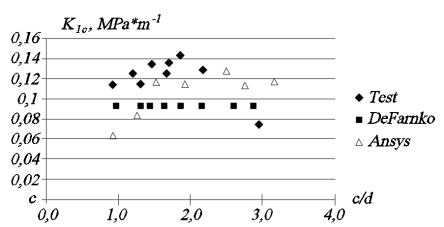
Рис. 8. График зависимости от

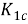
Заключение

Существует несколько сценариев разрушения морского льда. Каждому из них соответствуют свои скорости деформации и характер разрушения.

Если посмотреть, то можно сказать, что при полученных результатах исследования идет сильное завышение. Но если говорить о том, что лед настолько материал неоднородный по механическим свойствам, особенно при сжатии, с таким высоким коэффициентом вариации, отношении дисперсии к мат. ожидание, такой результат довольно хороший. Балочная теория, хотя и приводит к заниженному значению предельной нагрузки, все-таки с точностью до 30 % близка к тому, что демонстрирует лед.

Литература:

1. Abdelnour, R. 1981. Model Tests of Multi-year Pressure Ridges Moving onto Conical Structures. Proceedings IAHR Ice Symposium, Vol. 2, pp 728–751, Quebec City, Canada.
2. Blanchet, D. 1998. Ice Loads from First Year Ice Ridges and Rubble Fields. Canadian Journal of Civil Engineering. 25: 206–219.
3. Blanchet, D., Abdelnour, R. and Comfort, G. 1997. Mechanical properties of first year sea ice at Tarsiut Island. ASCE Journal of Cold Regions Eng. 11 (1): 59–83.
4. Brown, T.G. and Bruce, J.R. 1995. Finite Element Analysis of First Year Ridge Interactions. Report by Bercha & Assoc. to Public Works and Government Services Canada, Calgary, AL, Canada.
5. Brown, T.G., Cheung, M.S., Croasdale, K. R., and Wright, B. D, Advice on Design Ice Loads for the Northumberland Strait Bridge Piers. Report to Public Works and Government Services Canada, Charlottetown, PEI, 1995, 124p.
6. Bruneau, S. E., McKenna, R. F., Croasdale, K. R. and Crocker G. C. In-situ direct shear of ice rubble in first year ridge keels. Proceedings of 49th Canadian Geotechnical Conference. St. John’s September 1996.
7. Cornett, A.M. and Timco, G. W. Laboratory Tests on the Mechanical Properties of Saline Ice Rubble. NRC Controlled Report HYD-CTR-002, 1995, Ottawa, Ont. Canada.
8. Croasdale&Associates Ltd. 1995. Ice Load Models for First Year Pressure Ridges and Rubble Fields — Phase 1 Report. Joint Industry Government Project, Partly sponsored by the National Energy Board (PERD) and Public Works Canada.
9. Croasdale&Associates Ltd. Field Study of Ice Characteristics off the West Coast of Newfoundland. Report to National Research Council, Ottawa, and Exxon Production Research Co. PERD/CHC Report 2–70 and 2–71 (Proprietary), 1999.
10. Croasdale&Associates Ltd. In situ Ridge Strength Measurements — 1998. A study sponsored by NRC (PERD) and Exxon Production Research Co. (Proprietary until December 2001), 1998.
11. Croasdale&Associates Ltd., 1996. Ice Load Models for First Year Pressure Ridges and Rubble Fields. A Joint IndustryGovernment Project, Partly sponsored by PERD through the National Energy Board, Calgary, and supported by Mobil and Exxon.
12. Croasdale, K. R. 1997. Ice Structure Interaction: Current State of Knowledge &Implications for Future Developments. RAO Conference, St. Petersburg, Russia.
13. Croasdale, K. R. A Study of Ice Loads due to Ridge Keels. Proc. 4th Intl. Conf. on Development of Russian Offshore (RAO), St. Petersburg, 1999. 14. Eranti, E., Lehmus, E. and Nortala-Hoikkanen, A. 1992. First-Year Ice Ridge Characteristics and Loads on Offshore Structures. Proceedings ISOPE’92, Vol. II, pp 681–687, San Francisco, USA.
14. Nadreau, J. P. and Michel, B. Ice Properties in Relation to Ice Forces. Proc. 2nd IAHR State of Art Report on Ice Forces. 1984. Vol. 4, IAHR Symposium, Hamburg, 1984. 15
15. Shafrova, S., 2007. First-year sea ice features: Investigation of ice field strength heterogeneity and modelling of ice rubble behaviour. PhD thesis, Norwegian University of Science and Technology, Trondheim, Norway.
16. Smirnov, V., Sheikin I., Shushlebin A., Kharitonov V., Croasdale K. R., MetgeM., Ritch R., Polomoshnov A., Surkov G., Wang A, Beketsky S., Weaver J. S. Large scale strength measurements of ice ridges; Sakhalin 1998. // Proceedings of International Conference on ICETECH-2000, S.-Petersburg, 2000. P. 512–520.
17. Strub-Klein, L. and Sudom, D. A comprehensive analysis of the morphology of first year sea ice ridges, Cold Regions Science and Technology, 82, 2012, PP 94–109.
18. Timco, G. and Burden R. P. An Analysis of the Shapes of Sea Ice Ridges, Cold Regions Science and Technology 25(1), January 1997.
19. Timco, G. W., Croasdale K. and Wright B. An Overview of First-Year Sea Ice Ridges. Technical Report HYD-TR-047 PERD/CHC Report 5–112, 2000, 160 p.
20. Timco, G. W., Funke E. R., Sayed M. and Laurich P. H. 1992. A Laboratory Apparatus to Measure the Behaviour of Ice Rubble. Proc. OMAE 1992, Calgary, Al, Canada, Vol. IV, PP 369–375.