Автор предлагает экономическую модель распределения потоков отходов предприятий гостиничного и ресторанного бизнеса. Ее использование специализированными транспортными компаниями позволит значительно снизить удельные суммарные затраты на вывоз отходов и получить максимальную прибыль.
Ключевые слова: отходы, перевозки, прибыль, модель, потоки.
В странах Западной Европы отходы предприятий гостиничного и ресторанного бизнеса (ОПГРБ) воспринимают, прежде всего, как ценный источник получения вторичных материальных ресурсов. Основная проблема, связанная с обращением с отходами, заключается в их сортировке. За границей пришли к выводу, что гораздо эффективнее с экономической и экологической точки зрения сортировать отходы самим заказчикам [1, с. 78].
Государственная политика Российской Федерации в области экологии в настоящее время направлена на активное развитие в стране системы сбора, переработки и использования вторичных ресурсов.
Рассматривается довольно типичный случай, когда транспортировка отсортированного предприятиями гостиничного и ресторанного бизнеса вторсырья на мусороперегрузочные станции (МПС) осуществляется мусоровозами со съемными кузовами (бункеровозами) по маятниковым маршрутам. На МПС проводится обработка вторсырья, после которой спрессованные брикеты погружают в автотранспорт большой грузоподъемности и отвозят транспортными мусоровозами в пункты приема вторсырья.
Специализированная организация, осуществляющая вывоз ОПГРБ, покупает у клиентов отсортированное ими вторсырье определенного вида, отвозит на собственные МПС и впоследствии перепродает пунктам приема вторсырья.
Известно:
m — количество клиентов (предприятий гостиничного и ресторанного бизнеса);
n — количество МПС;
p — количество пунктов приема вторсырья;
Q iA — объем вывоза вторсырья от i-го клиента;
Q jBmax — максимальные объемы поставок в j-ю МПС;
Q kCmax — максимальный объем поставок для k-го пункта приема вторсырья;
С jB — себестоимость обработки 1 м 3 вторсырья в j-й МПС;
C kC — стоимость покупки 1 тонны вторсырья в k-м пункте приема вторсырья;
C iA — стоимость покупки 1 м 3 отсортированного вторсырья у i-го клиента;
C AB — себестоимость транспортировки 1 м 3 вторсырья на 1 км от клиента до МПС;
C BC — себестоимость транспортировки 1 м 3 вторсырья на 1 км от МПС до пункта приема вторсырья;
y j — коэффициент уплотнения вторсырья в j-й МПС;
p j — средняя плотность вторсырья в брикетах после уплотнения в j-й МПС;
L ijAB — расстояние от i-го клиента до j-й МПС;
L jkBC — расстояние от j-й МПС до k-го пункта приема вторсырья.
Необходимо осуществить такое распределение материальных потоков ОПГРБ между клиентами и МПС, МПС и пунктами приема вторсырья, при котором прибыль организации, осуществляющей вывоз отходов, будет максимальной.
Целевая функция прибыли учитывает затраты на транспортировку вторсырья S тр , его обработку на мусороперегрузочных станциях S обр и покупку предварительно отсортированного вторсырья у клиентов S отс , а также доход от продажи вторсырья D втор .
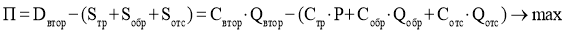
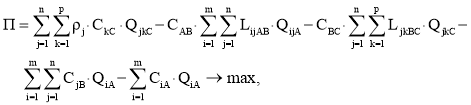
где Q ijA — объем перевозок отходов (вторсырья) от i-го заказчика в j-ю МПС;
Q jkC – объем перевозок отходов (вторсырья) с j-й МПС в k-й пункт приема вторсырья.
Из-за специфических особенностей рассматриваемого вывоза вводится система ограничений:
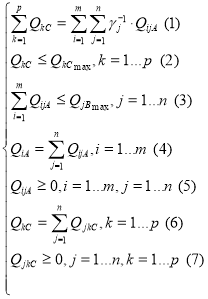
В уравнении (1) представлено соответствие между суммарным количеством завезенных в пункты приема вторсырья отходов и суммарным количеством отходов, вывезенных от предприятий гостиничного и ресторанного бизнеса.
Неравенство (2) означает, что суммарное количество отходов, завозимых в каждый из пунктов приема вторсырья, не должно превышать максимальных объемов поставок.
Из неравенства (3) следует, что суммарное количество отходов, завозимых в каждую из МПС, не превышает максимальных объемов поставок.
Уравнение (4) означает, что от каждого клиента отходы могут быть завезены на любую из мусороперегрузочных станций.
Из условия (5) следует, что количество отходов, перевозимых от каждого из клиентов на каждую из МПС, является величиной неотрицательной.
Уравнение (6) означает, что с каждой МПС отходы могут быть завезены в любой из пунктов приема вторсырья.
Из неравенства (7) следует, что количество отходов, перевозимых с каждой МПС в каждый из пунктов приема вторсырья, является величиной неотрицательной.
Заключение
Используя представленную модель, транспортная компания сможет рассчитать, какой объем отходов нужно перевезти от каждого предприятия гостиничного и ресторанного бизнеса на каждую МПС, а также с каждой МПС в каждый пункт приема вторсырья, чтобы снизить удельные суммарные затраты на вывоз отходов и получить максимальную прибыль.
Литература:
- Матросов, А. С. Управление отходами / А. С. Матросов. — М.: Кнорус, 2019. — 480 с.

