Рассматривается аппаратная реализация быстродействующего устройства приведения чисел по модулю, где в формирователях частичных остатков (ФЧО) используется вычитание модуля Р и кратных модуля Р. Значение вычитаемого определяется схемами сравнения, что позволяет минимизировать число сумматоров. На основе разрабатываемого формирователя частичных остатков построено быстродействующее устройство приведения чисел по модулю.
Ключевые слова: приведение по модулю, кратные модуля, формирователь частичных остатков.
Разработка быстродействующих операционных блоков аппаратных криптопроцессоров для ассиметричного шифрования является актуальной задачей, несмотря на их высокую стоимость [1].
В ассиметричных криптоалгоритмах наиболее критичной по времени базовой операцией является операция приведения по модулю. При аппаратной реализации приведения по модулю можно использовать различные теоретико-числовые методы вычисления остатка при делении на модуль Р, что приводит к различным структурам устройств [2÷8].
В работе [9] предложен алгоритм приведения числа по модулю с блокировкой отрицательных остатков на основе алгоритма деления чисел со сдвигом делимого. Для реализации предложенного алгоритма были разработаны формирователи частичных остатков (ФЧО), которые позволили построить матричные схемы устройства приведения чисел по модулю со сдвигом разрядов приводимого числа на один и на два разряда влево в сторону старших разрядов. В работе [10] рассмотрена схема приведения чисел со сдвигом на два разряда в сторону старших разрядов на основе ФЧО, где значение вычитаемого предварительно определялось введением в состав трех схем сравнения взамен двух сумматоров, что дало возможность оптимизировать состав логических схем ФЧО.
Одним из путей дальнейшего увеличения быстродействия устройства приведения чисел по модулю является сдвиг приводимого числа в сторону старших разрядов на три разряда на каждом шаге. При этом значение вычитаемого, производного от модуля, необходимо предварительно определять семью схемами сравнения, не используя сумматоры.
Основная часть. На рисунке 1 приведена структурная схема устройства, реализующего данный подход. Используется модифицированный алгоритм деления со сдвигом делимого, где на каждом шаге участвуют n+3 старших разрядов сначала делимого, а затем получаемых остатков. В состав устройства входит (2n+3)-разрядный сдвигающий регистр на три разряда влево РгА (2n разрядов основных, 3 разряда дополнительных), блок формирования кратных модуля Р, ФЧО, блок синхронизации Бл.СИНХ, в состав которого входит вычитающий счетчик СчТИ. На входы Бл.СИНХ подается сигнал «ПУСК», тактовый сигнал ТИ, двоичный код числа сдвигов K=log 2 (n/3), где n разрядность модуля.
Устройство работает следующим образом. По сигналу «ПУСК» приводимое 2n-разрядное число принимается в старшие разряды регистра РгА, а n-разрядный модуль Р принимается в блок формирования кратных модуля Р, где вырабатываются Р÷7Р и
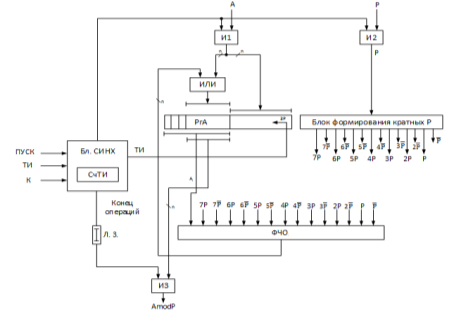
Рис. 1. Структурная схема устройства приведения числа по модулю со сдвигом приводимого числа на три разряда за такт
После приема операндов с выхода Бл.СИНХ на вход сдвига подается первый тактовый импульс ТИ1, который сдвигает на три разряда содержимое регистра РгА. И в старших n+3 разрядах РгА формируется значение А
1
=8R
0
+a
n-1
a
n-2
a
n-3
, которое передается на входы ФЧО. На другие входы передаются значения кратных модуля Р÷7Р и
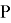
К моменту окончания формирования частичного остатка R 1 из Бл.СИНХ поступает тактовый импульс ТИ2, который сдвигает содержимое регистра РгА на три разряда влево, формируя значение А 2 , которое подается на входы ФЧО и на выходе формируется частичный остаток R 2 . С приходом каждого тактового импульса формируется A i и выполняется формирование очередного остатка R i .
После поступления каждого ТИ показания счетчика СчТИ уменьшается на единицу. При СчТИ=0 Бл.СИНХ вырабатывает сигнал «Конец операции», который задерживается на элементе задержки Л. З. на время записи последнего частичного остатка РгА. Этот частичный остаток является результатом. Результат из регистра РгА выводится на выход блока схем И3, задержанным сигналом «Конец операции».
Основным блоком устройства является ФЧО, который формирует остаток R i . ФЧО состоит из семи схем сравнения СС1÷СС7, сумматора СМ, логических схем И1÷И6, блоков логических схем ИЛИ1, И7÷И13, схемы ИЛИ2. Значение предыдущего остатка R i -1 , сдвинутое влево на три разряда с сторону старших разрядов, с присоединенным к нему очередными тремя младшими битами приводимого числа А, определяет значение

Предыдущим остатком в начале операции является значение n основных старших разрядов 2n-разрядного приводимого числа А. Значение A i подается на левые входы сумматора СМ и на левые входы схем СС1÷СС7, где A i сравнивается одновременно со значениями Р÷7Р, соответственно. В зависимости от результата сравнения на сумматоре СМ выполняется вычитание или Р, или одного из кратных модулей Р, что позволяет получить остаток R i <p. <="" p=""> </p.>
Если A i <Р, то R i =A i . В этом случае при сравнении на выходе 2 всех схем СС1÷СС7 формируется сигнал «0», который подается на входы схем И1÷И6, И13. В результате через блоки схем И7÷И13, ИЛИ1 на правые входы сумматора СМ инверсные значения Р÷7Р не подаются, вычитание на сумматоре СМ не выполняется, A i без изменения поступает на выход ФЧО.
Если A
i
≥Р при сравнении значения кода A
i
с
кодом модуля Р на СС-1, то на выходе 2 этой схемы формируется сигнал «1», который подается на вход схемы И1. Если A
i
<2P при сравнении значения кода A
i
с
кодом 2Р на СС-2, то выходе 1 этой схемы установится сигнал «1», который подается на второй вход схемы И1. И при выполнении условия Р≤A
i
<2Р на выходе И1 формируется единичный сигнал, который подается на вход схемы ИЛИ2 и на управляющий вход блока схем И7, что приводит к выполнению в сумматоре СМ операции R
i
=A
i
+
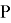
При сравнении значения кода A
i
с
кодом 2Р, если A
i
≥2Р, то на выходе 2 схемы СС-2 установится сигнал «1», который подается на первый вход схемы И2. При сравнении кода A
i
с
кодом 3Р, если A
i
<3P, то на выходе 1 схемы СС-3 установится сигнал «1», который подается на второй вход схемы И2. И при выполнении условия 2Р≤A
i
<3P на выходе схемы И2 формируется единичный сигнал, который подается на вход схемы ИЛИ2 и на управляющий вход блока схем И8, что приводит к выполнению в сумматоре СМ операции R
i
=A
i
+2
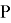
При сравнении кода A
i
с кодом 3Р, если A
i
≥3Р, то на выходе 2 СС-3 формируется сигнал «1», который подается на вход схемы И3. Одновременно A
i
сравнивается с 4Р, и если при этом A
i
<4P, то на выходе 1 схемы СС-4 формируется сигнал «1», который подается на второй вход схемы И3. Формируется сигнал «1», который подается на вход схемы ИЛИ2 и на управляющий вход блока схем И9, что приводит к выполнению в сумматоре СМ операции R
i
=A
i
+3
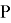
Аналогично формируется сигнал на выходе схемы И4 (4Р≤A
i
<5P). При этом сигнал «1» с выхода И4 подается на вход схемы ИЛИ2 и на управляющий вход блока схем И10, что приводит к выполнению на сумматоре СМ операции R
i
=A
i
+4
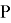
Таким же образом формируется сигнал на выходе схемы И5 (5Р≤Ai<6P). При этом сигнал «1» с выхода И5 подается на вход схемы ИЛИ2 и на управляющий вход блока схем И11, что приводит к выполнению на сумматоре СМ операции Ri=Ai+5
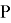
Аналогично формируется сигнал на выходе схемы И6 (6Р≤A
i
<7P). При этом сигнал «1» с выхода И6 подается на вход схемы ИЛИ2 и на управляющий вход блока схем И12, что приводит к выполнению на сумматоре СМ операции R
i
=A
i
+6
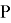
При условии A
i
>7P на выходе 2 СС-7 формируется сигнал «1», который подается на вход схемы ИЛИ2 и на управляющий вход блока схем И13, что приводит к выполнению сумматором СМ операции R
i
=A
i
+7
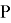
Заключение. Устройство приведения чисел по модулю с использованием кратных модуля и сдвигом приводимого числа на каждом шаге на три разряда влево в сторону старших разрядов позволяет ускорить процесс приведения по модулю за счет уменьшения количества шагов приведения по модулю, что требует дополнительных аппаратных затрат. Для сокращения аппаратных затрат в ФЧО для определения вычитаемых кратных модуля применены схемы сравнения. Если для этих целей в ФЧО применить сумматоры, то для этого потребовалось бы семь сумматоров, что приводит к большим аппаратным затратам.
Литература:
- Айтхожаева Е. Ж., Тынымбаев С. Т. Аспекты аппаратного приведения по модулю в ассиметричной криптографии. Вестник НАН РК, № 5 (2014). — Алматы: Наука, 2014. — c.88–93.
- Панкратова И. А. Теоретико-числовые методы в криптографии. — Томск: ТГУ, 2009. — 120 с.
- Ковтун М., Ковтун В. Обзор и классификация алгоритмов деления и приведения по модулю больших целых чисел для криптографических приложений. http://docplayer.ru/ 30671408-Obzor-i-klassifikaciya-algoritmov-deleniya-i-privedeniya-po-modulyu-bolshih-celyh-chisel-dlya-kriptograficheskih-prilozheniy.html. (18/02/2020)
- Петренко В. И. Кузьминов Ю. В. Умножитель по модулю. Пат. 2299461 РФ. Опубл.20.05.2007. Бюл. № 14.
- Копытов В. В., Петренко В. И., Сидорчук А. В. Устройство для формирования остатка по произвольному модулю от числа. Патент 2445730 РФ. Опубл.27.08.2011. Бюл. № 24.
- Орлов С. А., Цилькер Б. Я. Организация ЭВМ и систем: Учебник для вузов, 3-изд.-. СПб.: Питер, 2015. -688 с.
- Захаров В. М., Столов Е. Л., Шалагин С. В. Устройство для формирования остатка по заданному модулю. Патент 2421781 РФ. Опубл.20.06.2011. Бюл. № 17.
- Lambert RJ (2014) Method and apparatus for modulus reduction. Patent US No.08862651 B2.
- Tynymbayev S., Gnatyuk S. A., Aitkhozhayeva Y. Zh., Berdibayev R.Sh., Namazbayev T. A. Modular reduction based on the divider by blocking negative remainders. News of the National Academy of Sciences of the Republic of Kazakhstan. Series of Geology and Technical Sciences, № 2 (434). — Алматы: Наука, 2019. — с.238–248.
- Tynymbaev S. T., Berdibayev R.Sh., Omar T. К., Aitkhozhayeva Ye.Zh., Shaikulova A. A., Adilbekkyzy S. High-speed devices for modular reduction with minimal hardware costs. Cogent Engineering (2019), 6: 1697555.

