Многочисленные исследования педагогов и психологов показали, что ученик, плохо овладевший или не овладевший мыслительными операциями в начальных классах, в среднем звене обычно переходит в разряд неуспевающих. Главным решением этой проблемы является формирование условий, которые обеспечивают эффективное умственное развитие учащихся, связанное с формированием устойчивых познавательных интересов, творческой инициативы и самостоятельности в поисках способов решения задач. Для активной мыслительной деятельности очень полезны разные задачи, механизм решения которых обладает высоким мыслительным напряжением, самостоятельным поиском, доказательством, рассуждением. Отсутствие такой систе мы являе тся причиной низкого уровня сформированности у учащихся мыслительной деятельности. Поэтому на се годняшний де нь развитие мышления являе тся наиболе е острой пробле мой в обуче нии. В данной статье в качестве средства формирования приемов мыслительной деятельности представлены задачи на построение.
Как уже известно, при решении задач на построение пользуются четырехэтапной схемой решения:
- Анализ или поиск решения задачи.
На этом этапе, считая задачу решенной, т. е. искомую фигуру построенной, находят связь между данными и искомой фигурами.
- Построение.
На этом этапе указывается последовательность построений ПП и ОП, которые заканчиваются построением искомой фигуры. Поскольку все указанные построения с ПП и ОП могут быть выполнены с помощью
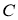
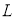
- Доказательство.
На этом этапе доказывается, что построенная фигура удовлетворяет всем требованиям задачи. Во многих случаях доказательство вытекает из хода построения.
- Исследование.
Исследование состоит в том, чтобы ответить на вопросы:
1) При всяком ли выборе данных задача имеет решение?
2) Сколько различных решений имеет задача при каждом возможном выборе данных?
При определении числа решений различают задачи на положение, в которых расположение искомой фигуры относительно данных играет существенную роль. В задачах же не на положение различные расположения искомой фигуры на плоскости роли не играют и принимаются за одно решение.
Одним из методов решения задач на построение является метод геометрических мест точек (метод пересечений). Рассмотрим данный метод более подробно.
Сущность метода состоит в следующем. Задачу сводят к построению одной точки
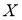
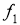
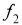

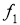
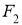
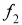
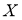
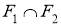

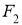
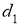
-
ГМТ, находящихся на данном расстоянии
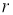
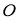
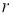
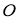
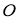
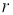
-
ГМТ, каждая из которых равноудалена от двух данных точек
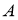
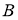
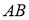
-
ГМТ, находящихся на данном расстоянии
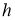
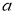
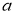
-
ГМТ, равноудаленных от двух данных параллельных прямых
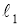
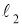
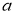
(
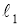
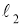
-
ГМТ, каждая из которых равноудалена от двух данных пересекающихся прямых
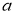
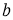
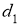
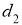
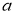
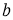
-
ГМТ, из которых данный отрезок
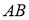
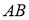
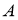
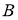
-
ГМТ, из которых данный отрезок
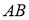
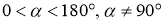
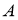
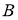
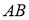
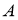
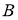
-
ГМТ середин хорд, отсекаемых данной окружностью
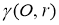
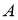
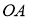
-
ГМТ, для которых разность квадратов расстояний от двух данных точек
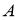
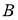
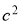
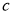
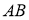
-
ГМТ, сумма квадратов расстояний, которых до двух данных точек
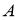
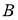
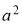
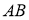
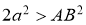
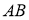
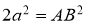
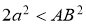
-
ГМТ, отношение расстояний которых до двух заданных точек
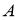
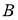
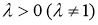
-
ГМТ середин равных хорд в данной окружности
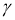
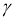
-
ГМТ, из которых данная окружность
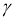
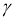
-
ГМТ, отрезки касательных из которых к данной окружности равны, есть окружность, концентрическая с
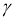
-
ГМТ, отрезки касательных каждой из которых к двум данным окружностям
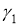
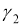
-
ГМТ, из каждой точки которого две данные окружности
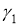
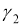
-
ГМТ, расстояния которых до двух пересекающихся прямых
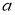
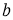
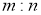
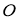
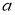
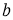
Иногда для определения точки достаточно построить одно геометрическое место, потому что другое дано в условии задачи. Если же искомая точка подчинена таким условиям, которые все в совокупности определяют только одно геометрическое место, то задача становится неопределённой.
Отсюда видно, как важно знать различные геометрические места. Знание геометрических мест иногда позволяет сразу видеть, где находится неизвестная точка.
Рассмотрим пример решения задачи на построение методом геометрических мест точек.
Задача. Постройте треугольник, если заданы сторона, прилежащий к ней угол и сумма двух других сторон.
Анализ. Пусть
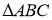
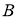
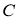
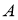
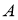
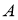
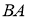
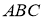
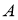
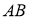
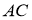
На продолжении стороны
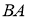
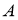
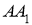
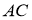
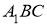
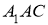
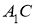
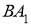
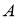
Построение.
1)построить
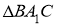
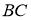
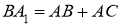
2)провести серединный перпендикуляр к стороне
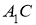
3)найти точку пересечения луча (
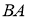
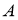
Доказательство.
В построенном
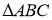
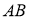
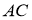
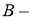
Исследование
проведём по ходу построения. Треугольник
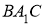
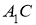
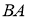
Приведем теперь систему элементарных задач на построение для решения которых используются рассмотренные геометрические места точек.
-
На данной прямой
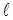
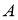
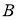
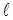
- Найти точку, равноудаленную от трех вершин треугольника.
- Найти точку, равноудаленную от трех сторон треугольника.
-
Данным радиусом описать окружность, походящую через данные точки
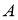
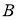
-
Построить точку, равноудаленную от точек
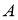
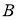
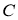
- Данным радиусом описать окружность, проходящую через данную точку и касающуюся данной прямой.
- Данным радиусом описать окружность, которая проходит через данную точку и касается данной окружности.
- Данным радиусом описать окружность, которая касалась бы данной прямой и данной окружности.
-
Построить окружность данного радиуса, касающуюся двух данных окружностей
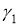
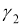
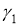
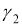
-
Данным радиусом описать окружность, которая от сторон данного угла отсекала бы хорды длины
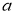
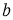
В заключени мы пришли к выводу, что задачи, решаемые методом геометрических мест точек, являются прекрасным материалом для отработки простейших геометрических преобразований, которые используются в более сложных методах: симметрия, гомотетия и т. д. Очевидно, что именно данный тип задач развивает у учащихся поисковые навыки решения, вводит их в посильное самостоятельное исследование, содействует выработке определенных геометрических представлений, а также более тщательной обработке умений и навыков. Большое значение имеет усвоение учащимися совокупной схемы решения задач на построение. Анализ, построение, доказательство и исследование точно соответствуют этапам любого логического рассуждения. Отметим, что необходимо уделять больше внимания изучению задач на построение, так как при грамотном использовании они являются мощным средством развития мыслительной деятельности учащихся. Поэтому материал данной работы может быть использован на факультативных занятиях по геометрии в общеобразовательных школах, начиная с 7 класса. Подобные задачи служат хорошим подспорьем при закреплении теоретических знаний по многим темам геометрии.
Литература:
- Хан Д. И. // Избранные теоремы планиметрии, задачи на построение. — Астана,2013.
- Шыныбеков А. Н., Шыныбеков Д. А. //Геометрия: Учебник для 7 кл.общеобразоват. школы.– Алматы:Атамұра, 2017.
- Шыныбеков А. Н., Шыныбеков Д. А., Жумабаев Р. А. // Геометрия: Учебник для 8 кл.общеобразоват. школы.– Алматы:Атамұра, 2018.
- Александров И. И. // Сборник геометрических задач на построение с решениями.– М.: КомКнига, 2010.
- Блинков А. Д., Блинков Ю.А // Геометрические задачи на построение– М:МЦНМО,2012.







