The paper discusses a comparison between Mathematical model and the Two Dimension Fast Fourier Transform (2- DFFT) Using some performance analysis such as Speed performance, Mean Square Error (MSE), Peak signal to noise ratio analysis (PSNR) and signal to noise ratio analysis (SNR).
Through the experiments and the results finding that the mathematical model is more accurate and better than the 2-DFFT method. The paper also reviews the histogram for all cases and results and the effect of the implementation of the two methods in the form of the image and its spectrum, noting that the effect is clear to the accuracy of the preferred method.
Keywords: mathematics module, 2-DFFT, SNR, PSNR, MSE.
Introduction
The rapid development of all industries, including the technology of the multimedia industry and telecommunications, led to an increase in the demand for storage, which calls for the transmission of information, including the transfer of digital images. Communication networks such as mobile networks and the Internet are sophisticated networks. However, they are public networks and are not suitable for direct transmission of confidential messages. So, it raising the concerns about data security and confidentiality if stored or transmitted over the Internet [1].
Protecting data confidentiality is one of the most important challenges facing us in contemporary times. In addition to the Illegal distribution and copying of digital documents and the unlawful release of confidential documents of unauthorized persons.
With the increasing use of the Internet through the use of smartphones and computer networks, [2–3] a huge amount of data, information, images, videos, and multimedia are transmitted daily. Hacking of this data by hackers is a possibility, so keeping this data in a way that prevents hackers from getting it has become very important.
Due to the development of advanced technologies in increasing the speed and storage of the Internet, the Internet has become huge storage and processing of data in all its forms. This action leads to the search for an appropriate and acceptable way to save data [4].
One of the solutions to this problem is the use of encryption technology (the process of converting information into non-understandable codes to prevent unauthorized persons from viewing or understanding them, and then re-converting the encrypted information to its original form using the appropriate key to decrypt) [5–7].
Fig. 1. Sample Encryption and Decryption Process
Digital image encryption manipulates a substantial part in the security of multimedia in storing and sending multimedia data. Encryption was used to facilitate secure data storage and confidential communication between users.
Encryption is typically used to protect information and data using certain algorithms. It is also used to protect data transmitted over networks, the Internet, mobile phones, media and wireless systems, Bluetooth devices, and other communications systems [8].
Many cryptographic algorithms are implemented using different methods. Where the original image is transformed into a non-readable image, and then returned with the least possible loss on the other side [9–11].
The encryption system consists of two main parts; the encryption process converts the original data (images) to encrypted data, the decryption converts the encrypted data to the original data. Where a specific key is only known by the authorized person.
Literature review
Many researchers have a huge amount of papers about the encryption, explained different kinds of it, as shown below:
Many image encryption algorithms are proposed for different formats like a PNG, TIFF, JPEG, and GIF. This approach used for permutation and diffusion in encryption [12–13], it is based on dividing the dynamic block of a 3D baker (using information hiding). It deals with high-performance product image (image recovered can be without losses). Obtained results indicate that security and speed are high.
An algorithm has a secret key designed used to uniform block cipher established on producing a dynamic nonlinear (mixing of the logistic methods and piecewise chaotic map awarding to primary values mood), by using operation of XOR. When applying a key generator algorithm High advantages are obtained (experimental results) [14–16].
From the correlation coefficient process (zero), and the entropy process (eight) the image encryption process is achieved (efficient). Leads to strong key with high security.
Minimizing the data transmission size and resist against any attacks need to implementing an encrypted algorithm. The acquired images firstly sampled by using a random matrix that achieves the encryption and changes the data size. Secondly, combining commutation and propagation to make a resist to noise and different attacks [17]. Rebuilding and decryption operations are applied to get back the original images. This approach indicated efficient security and the system hardiness [18].
Magnetic resonance imaging and medical signals, radar image production, analysis, filtering, and image compression, in addition to frequency estimation, etc. A lot of examples about using 2D FFT where these techniques are widely used in DSP.
The 2d Fast Fourier Transform is one of the important tools for image processing, almost it is utilized to analyze an image till her components (sine, &cosine) [19–20]. The domain equivalent is the locative input image, while transformation output represents the image in frequency domain. In FFT range image, each point appears a specific frequency implicated in the locative scope image.
The object is handled (two-dimensional) toward a digital application with 2D FFT usage. A two-dimensional matrix of pixels (numbers with complex values) Calculation. A problem working on a frequent algorithm of 2D FFT significantly increases the number of calculations, the period specified for a 2D signal, must immediately obtain a new spectrum when replacing one sample with a newer one [21–22].
Experimental Results
This approach is implemented by using the Matlab program and gray scale image (eight images data are prepared to be tested) of size 250× 250 are used to apply as a test image. The image should be of.jpg or.jpeg and.png image format. The two control parameters of the mathematical model are Z where {Z=16} and the initial value is 0.10.
Image Data: The dataset consists of nine images, the color image is used then converted into grey scale and double images.

Fig. 2: Nine images that consists the dataset
Histogram Analysis
The statistical properties of images can be represented using the histogram, which shows the apportionment of pixel accounts.
This analysis is performed to compare between histogram for the mathematical model and histogram for 2D-FFT. Will notice in the 2D-FFT uniform distribution of histograms in encrypted images for more original images while in mathematical model absolutely different from that of the plain-image as shown in Figure (3–4).
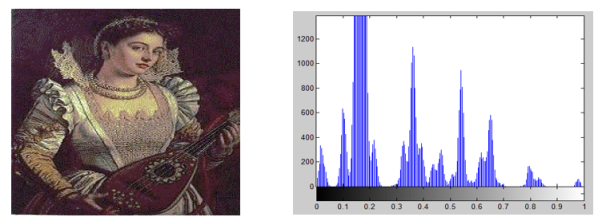
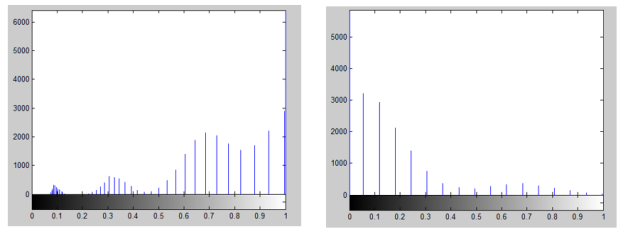
Figure (3) illustrates the histograms of the gray scale-original image, and after applying the mathematics model, Figure 3(a) offering the real image histogram, Figure 3(b) offering the log image histogram, and figure 3(c) offering the imaginary image histogram.
(a) Histogram of the original Image
(b) Histogram of the real image (c) Histogram of the log image
(d) Histogram of the imaginary image
Fig. 3. Histogram of the original, real, log and imaginary Image
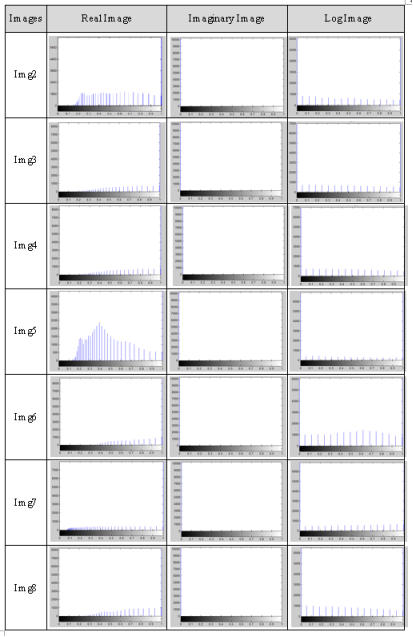
Fig. 4. Histogram after apply mathematics model
Figure (3) shows the histogram for all real, imaginary and log images after applying mathematics model.
Figure (4) shows the histogram of the gray image encoded after applying the 2D-FFT, the histogram for real image, log image and imaginary image.
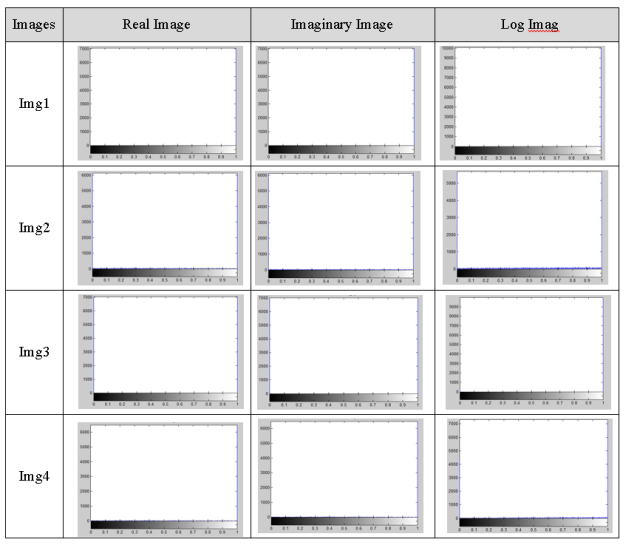

Fig. 5. Histogram after applying 2D-FFT
Performance analysis
1- Speed performance
Run-time is a very important aspect of a good algorithm, the time speed rate measured for several greyscale images of sized 256× 256 by using the proposed mathematical model and 2-DFFT algorithm.
The time analysis has been done on Computer with 4.00 GB of RAM memory Intel (R) Core (TM) i5–2540M, CPU@2.60 GHz processor running on the Windows7 operating system. The comparison between the mathematical model and 2-DFFT time speed are shown in Table 1. The average speed of time for the mathematical model is (0.582919292) while for 2D FFT is (0.54241067).
Table 1
Time speed (mathematical model and 2-DFFT)
|
images Z=16 |
Time speed (second) |
||
|
Math. model |
2-DFFT |
||
|
(Img1) |
|||
|
(Real Part) |
0.532991 |
0.567967 |
|
|
(Imaginary Part) |
0.613947 |
0.455396 |
|
|
(Log Part) |
0.577682 |
0.518816 |
|
|
(Img2) |
|||
|
(Real Part) |
0.592648 |
0.628340 |
|
|
(Imaginary Part) |
0.592269 |
0.522404 |
|
|
(Log Part) |
0.609018 |
0.587370 |
|
|
(Img3) |
|||
|
(Real Part) |
0.549968 |
0.525182 |
|
|
(Imaginary Part) |
0.592865 |
0.580731 |
|
|
(Log Part) |
0.553967 |
0.587883 |
|
|
(Img4) |
|||
|
(Real Part) |
0.536572 |
0.575336 |
|
|
(Imaginary Part) |
0.611902 |
0.587792 |
|
|
(Log Part) |
0.567373 |
0.566099 |
|
|
(Img5) |
|||
|
(Real Part) |
0.598053 |
0.596881 |
|
|
(Imaginary Part) |
0.561062 |
0.502492 |
|
|
(Log Part) |
0.604715 |
0.449769 |
|
|
(Img6) |
|||
|
(Real Part) |
0.547027 |
0.566263 |
|
|
(Imaginary Part) |
0.611481 |
0.574422 |
|
|
(Log Part) |
0.587898 |
0.583376 |
|
|
(Imag7) |
|||
|
(Real Part) |
0.642028 |
0.555690 |
|
|
(Imaginary Part) |
0.542860 |
0.455730 |
|
|
(Log Part) |
0.579677 |
0.479860 |
|
|
(Imag8) |
|||
|
(Real Part) |
0.588974 |
0.536695 |
|
|
(Imaginary Part) |
0.564270 |
0.455235 |
|
|
(Log Part) |
0.630816 |
0.558127 |
|
2- Mean Square Error (MSE)
To know what is the difference between the original and the encrypted image using parameter Mean Square Error (MSE). Table 2 shows the MSE of the encrypted image using a mathematical model and encrypted image using 2-DFFT.
3- Peak signal to the noise ratio dissection (PSNR) and signal to the noise ratio dissection (SNR)
The PSNR and SNR values between the original image and the encrypted one listed in Table below. To show this more obviously runing the above parameters as follow:
PSNR = 10*log10(256*256/MSE)
SNR= 10*log10(PSNR^2/MSE)
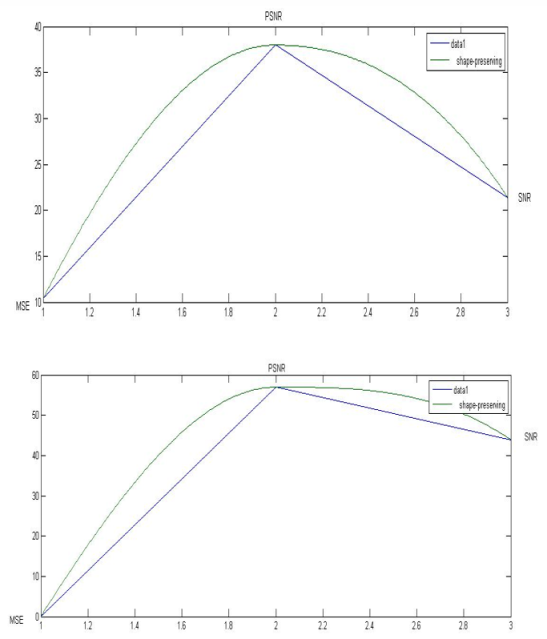
Fig. 6: Image 1 and 2
Table 2
MSE, PSNR, and SNR (mathematical model and 2-DFFT)
|
Images |
Mathematical model |
2D FFT |
||||||
|
Type image |
MSE |
PSNR |
SNR |
MSE |
PSNR |
SNR |
||
|
Img1 |
(Real Part) |
0.13 |
56.96 |
43.91 |
7599.82 |
9.36 |
19.39- |
|
|
(Imaginary Part) |
0.13 |
57.10 |
44.07 |
776.36 |
19.26 |
3.21- |
||
|
(Log Part) |
0.68 |
49.83 |
35.61 |
3.94 |
42.21 |
26.55 |
||
|
Img2 |
(Real Part) |
10.41 |
37.99 |
21.42 |
4698.95 |
11.44 |
15.55- |
|
|
(Imaginary Part) |
0.09 |
58.71 |
45.92 |
1079.06 |
17.83 |
5.31- |
||
|
(Log Part) |
1.02 |
48.09 |
33.57 |
1.17- |
47.49 |
33.20 |
||
|
Img3 |
(Real Part) |
242361.72 |
5.68- |
38.76- |
14370.49 |
6.59 |
25.20- |
|
|
(Imaginary Part) |
0.26 |
54.07 |
40.56 |
2454.58 |
14.27 |
10.81- |
||
|
(Log Part) |
33.32 |
32.94 |
15.13 |
2.75 |
43.77 |
28.43 |
||
|
Img4 |
(Real Part) |
733.34 |
19.51 |
2.85- |
12998.67 |
7.03 |
24.21- |
|
|
(Imaginary Part) |
0.22 |
54.65 |
41.23 |
1737.64 |
15.77 |
8.45- |
||
|
(Log Part) |
8.47 |
38.89 |
22.52 |
0.23 |
54.56 |
41.40 |
||
|
Img5 |
(Real Part) |
269.20 |
23.86 |
3.25 |
5360.09 |
10.87 |
16.56- |
|
|
(Imaginary Part) |
0.10 |
58.37 |
45.53 |
893.27 |
18.65 |
4.09- |
||
|
(Log Part) |
6.66 |
39.93 |
23.79 |
1.07 |
47.87 |
33.64 |
||
|
Img6 |
(Real Part) |
10.89 |
37.80 |
21.18 |
12946.44 |
7.04 |
24.17- |
|
|
(Imaginary Part) |
0.24 |
54.41 |
40.96 |
2599.59 |
14.02 |
11.22- |
||
|
(Log Part) |
0.88 |
48.72 |
34.31 |
0.05 |
61.15 |
48.92 |
||
|
Img7 |
(Real Part) |
14.90 |
36.43 |
19.40 |
8883.70 |
8.68 |
20.72- |
|
|
(Imaginary Part) |
0.16 |
56.23 |
43.06 |
1352.00 |
16.86 |
6.78- |
||
|
(Log Part) |
1.25 |
47.21 |
32.53 |
0.25 |
54.14 |
40.66 |
||
|
Img8 |
(Real Part) |
53697.19 |
0.87 |
48.56- |
8891.85 |
8.67 |
20.72- |
|
|
(Imaginary Part) |
0.15 |
56.35 |
43.21 |
1056.69 |
17.93 |
5.17- |
||
|
(Log Part) |
26.06 |
34.00 |
16.47 |
0.98 |
48.23 |
33.74 |
||
Conclusion
The paper proved after much implementation of the program and a set of digital images the following conclusions:
— MSE in Imaginary part is lower than from MSE in 2DFFT.
— PSNR in Imaginary part is higher than PSNR in 2DFFT.
— The average speed of time for the mathematical model is (0.582919292) while for 2D FFT is (0.54241067).
Thus the discussion showed the preference and efficiency of the mathematical model.
References:
- Mondal, Arindam, and Amanpreet Kaur. «Comparative Study of Feature Level and Decision Level Fusion in Multimodal Biometric Recognition of Face Ear and Iris». International Journal of Computer Science and Mobile Computing (IJCSMC) 5.5 (2016): 822–842.
- Iwok, I. A., and G. M. Udoh. «A Comparative Study between the ARIMA-Fourier Model and the Wavelet model». American Journal of Scientific and Industrial Research 7.6 (2016): 137–144.
- Al-Ani, Muzhir Shaban. «Efficient Image Encryption Approach Based on Chaos Technique». IOSR Journal of Electrical and Electronics Engineering (IOSR-JEEE) 12.3 (2017): 54–60.
- Abu-Amara, Fadi, and Salam A. Hoshang. «ROBUST CHAOS VIA DOME LOGARITHMIC MAP».
- L. Liu, S. Miao, H. Hu, M. Cheng, «N-phase Logistic Chaotic Sequence and Its Application for Image Encryption», IET Signal Processing, vol. 10, no. 9, pp. 1096–1104, 2016.
- Y. Şekertekin, Ö. Atan, «An Image Encryption Algorithm Using Ikeda And Henon Chaotic Maps», 24th Telecommunications Forum TELFOR, pp. 1–4, 2016.
- Z. Ni, X. Kang, L. Wang, «A Novel Image Encryption Algorithm Based on Bit-Level Improved Arnold Transform and Hyper Chaotic Map» IEEE International Conference on Signal and Image Processing, pp. 156–160, 2016
- Y. Song, J. Song, «A Secure Image Encryption Algorithm Based on Multiple One-dimensional Chaotic Systems» 2016 2nd IEEE International Conference on Computer and Communications, pp. 584–588, 2016.
- W. Zhu, Y. Shen, «Encryption Algorithms Using Chaos and CAT Methodology» Anti-Counterfeiting Security and Identification in Communication (ASID), 2010 International Conference, 2010, pp. 20–23.
- V. Patidar, N. K. Pareek, G. Purohit, and K. K. Sud, «A Robust and Secure Chaotic Standard Map Base Pseudorandom Permutation Substitution Scheme for Image Encryption» Opt. Commun., vol. 284, no. 19, pp. 4331–4339, 2011.
- A. Jolfaei, A. Mirghadri, «An Image Encryption Approach Using Chaos and Stream Cipher» Journal of Theoretical and Applied Information Technology 2010.
- T. Xiang et al., «A Novel Block Cryptosystem Based on Iterating a Chaotic Map» Phys. Lett. A, vol. 349, 2006, pp. 109–115.
- Q. Wang, Q. Ding, Z. Zhang, L. Ding, «Digital Image Encryption Research Based on DWT and Chaos» Natural Computation, 2008. ICNC '08. Fourth International Conference Vol. 5, 2008, Pages 494–498.
- G. J. Zhang, Q. Liu, «A Novel Image Encryption Method Based on Total Shuffling Scheme» Optics communications, 284, pages. 2775–2780 (2011)
- S. Koppu, V. Madhu Viswanatham, «A Fast Enhanced Secure Image Chaotic Cryptosystem Based onHybrid Chaotic Magic Transform», Hindawi Publishing Corporation, Modelling and Simulation in Engineering, Published 4 January 2017, Article ID 7470204, pp.1–12.
- L. Mohammed Jawad, G. Sulong, «A Novel Dynamic Secret Key Generation for an Efficient Image Encryption Algorithm», Modern Applied Science; Vol. 9, No. 13; 2015, pp. 85–97.
- J. Kumar, S. Nirmala, «A Novel and Efficient Method Based on Knight Moves for Securing the Information Contents of Images: A Parallel Approach», Journal of information security and applications 30 (2016) pp. 105–117
- Mohmmed, Haider Ahmed, Layth Mohammed Abd Ali, and Othman M. Hussein Anssari. «Maintaining Electric Power Quality Using Integrated S-Transform with Xenogeneic Composition Neural Network». International Journal of Engineering & Technology 7.3.20 (2018): 538–543.
- C. Sivapong Nilwong, W. San-Um, «An Image Encryption Scheme and Its Android Application Using Robust Chaotic Map with Absolute Value Nonlinearity», ITMSOC Transactions on Information Technology Management 01 (2016) pp. 26–32.
- M. Kumar, A. Iqbal, P. Kumar, «A New RGB Image Encryption Algorithm Based on DNA Encoding and Elliptic Curve Diffie Hellman Cryptography», Signal Processing, 125 (2016) pp. 187–202.
- D. Xiaoa, L. Wang, Tao Xiang, Yong Wang, «Multifocus Image Fusion and Robust Encryption Algorithm Based on Compressive Sensing», Optics & Laser Technology 91 (2017) pp. 212–225.
- M. Zhang, X. Tong, «Joint Image Encryption and Compression Scheme Based on IWT and SPIHT», Optics and Lasers in Engineering 90 (2017) pp. 254–274







