Расчет систем тягового электроснабжения является основной задачей проектирования электрифицированных железных дорог. Выбор количества питающих линий, уставок защит, силового оборудования тяговых подстанций и линий обратного тока основывается на расчетных токах нормального режима нагрузки с различной парностью движения и режимов короткого замыкания. Производство необходимых расчетов выполняется, на современном этапе, на основе компьютерной модели проектируемого участка.
MatLab/Simulink является одной из наиболее удобных и эффективных программ для инженерных расчетов и может быть использован для моделирования систем тягового электроснабжения, так как включает в себя большой набор расчетных методов, обширную библиотеку силовых электротехнических элементов и имеет возможность создания сложных моделей.
Задачи
Первичными данными для проектирования являются параметры электрифицированного участка (длина участка, эквивалентный уклон, внутреннее сопротивление тяговой подстанции, напряжение холостого хода подстанции, мощность или ток короткого замыкания на вводах, пикетаж объектов электроснабжения и остановочных пунктов, тип и масса подвижного состава, марки тяговых трансформаторов, преобразовательных агрегатов, фидеров, отсосов и т. д.) и система тока.
Тяговый расчет электроподвижного состава.
На основе данных, указанных выше, производится тяговый расчет, в ходе которого определяются зависимости тока ЭПС и его скорости от времени хода по участку. Пример результатов упрощенного тягового расчета представлен на рисунке 1.
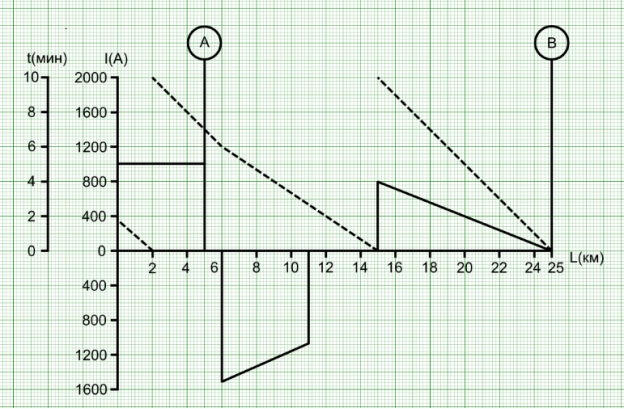
Рис. 1. Результаты упрощенного тягового расчета
Далее составляется схема замещения системы тягового электроснабжения (см. рис. 2) в которую входят: система внешнего электроснабжения, модели тяговой подстанции, линии контактной сети, рельсовой цепи и электроподвижного состава с исполненным тяговым расчетом.
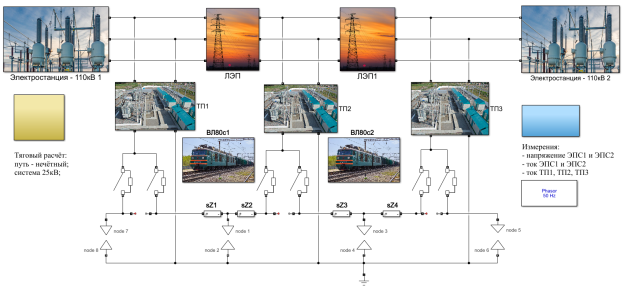
Рис. 2. Представление схемы замещения СТЭ в виде виртуальной модели, выполненной в среде Matlab/Simulink
Блочная структура модели:
1) Внешнее электроснабжение
a) Электростанции — первичные источники напряжения (110 кВ переменного тока).
b) Линии электропередач (ЛЭП) — система проводов, выполняющая функцию передачи электроэнергии на расстояние.
2) Тяговые подстанции
3) Контактная сеть
4) Электроподвижной состав
5) Вспомогательные блоки
a) Блоки контактов контактной сети и рельса (на модели node) — устанавливают электрическое соединение между контактной сетью и ЭПС.
b) Блок Тяговый расчет
c) Блок Измерения — измерительные приборы для мониторинга тока и напряжения на токоприемнике ЭПС.
При моделировании контактной сети и ЭПС в электрической схеме замещения возникает сложность, обусловленная тем, что в специализированной библиотеке SimPowerSystems MatLab/Simulink нет блоков, моделирующих перемещающуюся нагрузку, которой является ЭПС.
Решение данной проблемы
Эту задачу необходимо разделить на две подзадачи: движение по участку без узлов в схеме замещения и переход с одной зоны питания на другую.
Первая подзадача:
Контактная сеть имеет погонное сопротивление, следовательно, сопротивление от узла схемы до движущегося ЭПС будет изменяться. Изменение этого сопротивления и будет моделировать “движение” ЭПС от одного узла к другому. В качестве узлов схемы могут выступать точки присоединения тяговых подстанций, постов секционирования, пунктов параллельного соединения и т. д. к контактной сети.
Запишем уравнение, которое описывает изменение тока в элементе контактной сети в зависимости от напряжения на этом элементе, в виде:
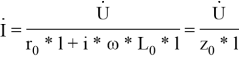
где
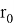
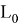
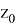
Эту формулу реализуем в MatLab/Simulink следующим образом:
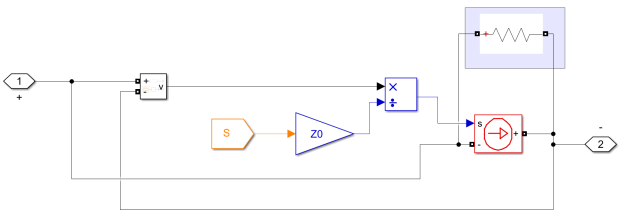
Рис. 3. Реализация изменения сопротивления в блоке контактной сети
Координата S (см. рис. 3), приходящая из блока ЭПС умножается на погонное сопротивление контактной сети, что дает полное сопротивление от узла слева до текущего положения ЭПС. С помощью вольтметра (блок Voltage Measurement) снимается напряжение на элементе контактной сети, а с помощью блока Divide производится деление на полное сопротивление. В ходе деления получаем значение тока, которое поступает на Controlled Current Source.
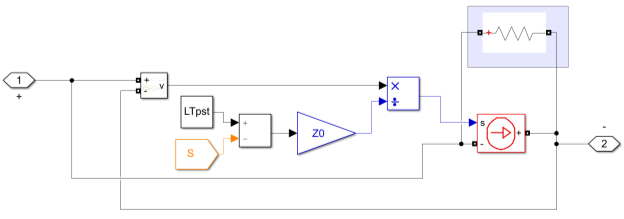
Рис. 4. Реализация уменьшающегося сопротивления в блоке контактной сети
В еще одном блоке контактной сети реализуется уменьшающееся сопротивление от ЭПС до узла справа.
Вторая подзадача:
При переходе с одной питающей зоны на другую, схема электроснабжения кардинально меняется. Поэтому для непрерывного моделирования необходимо создать возможность для автоматического переключения ЭПС на другую зону питания (см. на рис. 5).
Блок MATLAB Function (см. рис. 6) создает массив, размерность которого определяется количеством межподстанционных зон (количество тп -1) и определяет состояние переключателей.
Если координата поезда больше или равна координате второй подстанции и меньше или равна координате третьей подстанции, то в первую ячейку подстанции записывается 0, а во вторую 1.
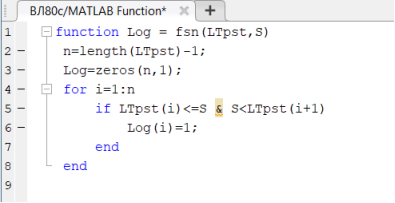
Рис. 5. Скрипт блока управления
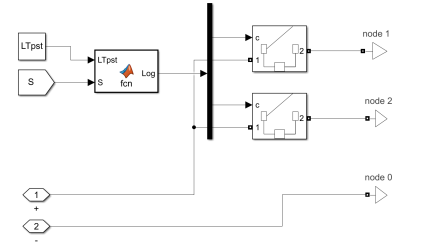
Рис. 6. Блок управления и блок контакторов
С помощью блока Demux сигнал отправляется на выключатели Breaker, которые подключаются при помощи блока Neutral к определенному участку контактной сети. Минус всегда подключен к node 0-рельсу.
На предложенной модели были выполнены расчеты и получены зависимости токов подстанций и напряжений на токоприемнике ЭПС от времени (см. рис.7).
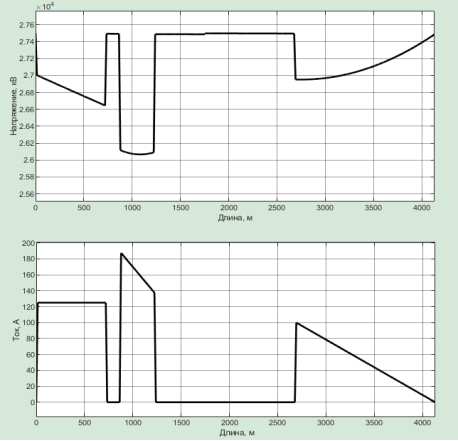
Рис. 7. Осциллограммы напряжения на токоприемнике и тока электровоза
Проверка корректности выполненных вычислений
Чтобы удостовериться в грамотном выполнении вычислений, алгебраически сложим все токи тяговых подстанций, при верных вычислениях, их сумма должна быть равна току ЭПС.
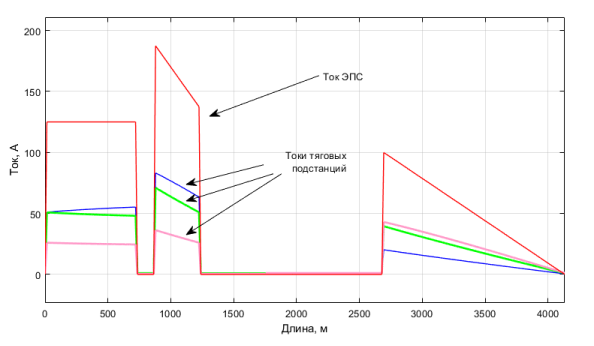
Рис. 8. Проверка корректности вычислений с помощью осциллограмм токов тяговых подстанций и тока ЭПС
Как видно из графика (см. рис. 8), алгебраическая сумма токов тяговых подстанций равна току ЭПС, это свидетельствует корректности результатов, полученных в результате моделирования.
Вывод
Таким образом, в ходе исследований была реализована модель, учитывающая перемещающуюся переменную нагрузку. На основании предложенной модели была решена задача, как разработка расчёта СТЭ с учетом непрерывного перемещения ЭПС по проектируемому участку. Результаты моделирования корректны, что подтверждено в конце вычислений проверкой графическим методом.

