В статье автор оценивает ток утечки МДП-транзистора, используя формулу Фаулера — Нордгейма.
Ключевые слова: токи утечки, напряженность, полевой транзистор, плотность тока Пула — Френкеля
Введение
Физика низкоразмерных структур — актуальная и динамично развивающаяся область современной физики твердого тела. При переходе к системам нанометрового масштаба квантовые эффекты играют ключевую роль в функционировании приборов на их основе [1–5]. В данной работе проводится сравнительный анализ туннельного тока в функционировании современных полевых транзисторов. Объектом исследования является туннельный ток.
Ток Фаулера-Нордгейма в МДП-транзисторе
Для численной оценки тока утечки МДП-транзистора используют формулу Фаулера-Нордгейма [4]. Эта формула позволяет рассчитать туннельный ток в квазиклассическом приближении в присутствии электрического поля:
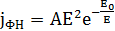
Здесь E — напряженность электрического поля в тонком слое диэлектрика. Значения констант для материалов SiO2 — Si равны:
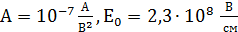
В работе рассчитаны значения плотности тока (механизм Фаулера-Нордгейма) для разных значений напряженности электрического поля между затвором и каналом МДП-транзистора. На рисунке 1 представлен график зависимости тока утечки
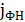
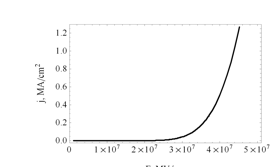
Рис. 1. График зависимости тока утечки от напряженности
Незначительное увеличение напряженности электрического поля вызывает заметный рост тока утечки.
Эффект Пула-Френкеля
Суть эффекта заключается в понижении барьера кулоновского потенциала при воздействии электрического поля, что приводит к увеличению концентрации носителей тока. Для расчета плотности тока Пула-Френкеля используют формулу [3]:
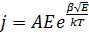
где:
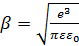
Для вычисления зависимости используем нормировку:
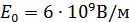
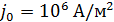
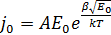
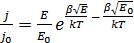
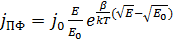
На рисунке 2 представлен график зависимости плотности тока Пула-Френкеля от напряженности электрического поля.
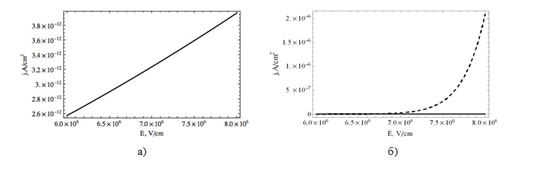
Рис. 2. a) График зависимости тока Пула-Френкеля от напряженности при T=300K; б) сравнение графиков зависимости плотности тока Фаулера-Нордгейма (пунктирная линия) и тока Пула-Френкеля (сплошная линия) от напряженности
Из графиков видно, что ток Пула-Френкеля оказывает незначительное влияние на работу транзистора в отличие от тока Фаулера-Нордгейма.
Современные транзисторы могут работать только в определенных пределах значений напряженности. Для полевого транзистора с толщиной диэлектрика из диоксида кремния в 0.15 мкм этот предел равен
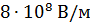
Проиллюстрируем зависимость плотности тока Пула-Френкеля от температуры в доступных для транзистора пределах напряженности (рис. 3).
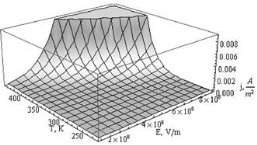
Рис. 3. График зависимости плотности тока Пула-Френкеля от напряженности электрического поля и от температуры
Расчеты показывают, что при большем значении абсолютной температуры резкое возрастание плотности тока Пула-Френкеля происходит при меньшем значении напряженности электрического поля.
Заключение
В работе проведен расчет туннельного тока утечки (механизмы Фаулера — Нордгейма и Пула — Френкеля) в современном МДП-транзисторе. Сравнительные численные оценки, проведенные в данной работе, показали:
1) ток Пула-Френкеля дает малый вклад в токи утечки современных нанотранзисторов;
2) ток Фаулера-Нордгейма при фиксированном значении напряженности не зависит от толщины диэлектрика;
3) с ростом напряженности электрического поля ток утечки Фаулера-Нордгейма резко возрастает, что негативно сказывается на работе устройств на основе МОП-транзисторов;
4) с ростом температуры ток Пула-Френкеля, появление которого так же негативно влияет на работу транзистора, возрастает при меньших значениях напряженности.
Литература:
- Афонский А. А., Дьяконов В. П. Электронные измерения в нанотехнологиях и в микроэлектронике. — М.: — ДМК Пресс, 2011. — 688 с.
- Кобаяси Н. Введение в нанотехнологию. — М.: Бином, 2005. — 134 с.
- Минько Н. И., Строкова В. В. Методы получения и свойства нанообъектов — М.: ФЛИНТА, 2013. — 165 с.
- Mark Lundstrom, Jing Guo. Nanoscale Transistors. Springer, 2006. — 213 с.
- Scanning Probe Microscopy and Spectroscopy: Theory, Techniques, and Applications Ed. Dawn Bonnell Wiley-VCH; 2 edition, 2000. — 493 с.

