В настоящее время оценочной процедурой Всероссийской системы качества образования в начальной школе являются: Всероссийские проверочные работы.
Цель ВПР — обеспечение единства образовательного пространства Российской Федерации и поддержки введения Федерального государственного образовательного стандарта за счет предоставления образовательным организациям единых проверочных материалов и единых критериев оценивания учебных достижений.
Нужно помнить о том, что Всероссийские проверочные работы не являются итоговой аттестацией обучающихся начальной школы , а представляют собой аналог годовых контрольных работ, традиционно проводившихся ранее в школах. Всероссийские проверочные работы лишь часть проверочных работ.
Но, несмотря на это, целью работы каждого педагога является подготовить учащихся к комплексным работам на должном уровне.
Опыт подсказал, что подготовка не должна быть самоцелью (школа призвана учить, а не готовить к сдаче экзамена), но в то же время проходить постоянно, но не натаскиванием на тестирование, а в ходе планомерного использования тестов в течение нескольких лет школьного обучения. И от того, насколько грамотно построена работа, будет зависеть результат.
Главная задача учителя — учить учиться, сделать так, чтобы ученики умели и хотели самостоятельно добывать знания, находить решение нестандартных задач, применять полученные знания в реальной жизни. Поэтому, моя позиция — учитель-помощник, как и предполагает технология «Педагогических мастерских», по которой работает мой класс. Думаю, что этим и определяется мой выбор стратегии и тактики в системе подготовки к комплексным работам и ВПР.
Для успешного выполнения Всероссийских проверочных работ необходима системная работа по освоению предметных знаний и формированию универсальных учебных действий с 1 по 4 класс.
Подготовка к ВПР ведется мною, начиная с первого класса, не только на уроках русского языка, математики, окружающего мира и литературного чтения, но и на внеурочных занятиях (Кружок «Логика») и неаудиторных занятиях. С отстающими и слабоуспевающими детьми проводятся индивидуальные занятия. В своей работе использую как индивидуальную, так и групповую форму работу с детьми, включают разнообразные методы и приёмы: тестовые работы, индивидуальные и групповые карточки, организую пробное тестирование.
Особое внимание уделяем заданиям повышенной сложности: математика (10.11), русский (к ним можно отнести задания по работе с текстом), окружающий мир (составление логических цепочек…). Наиболее удобны для этого, на мой взгляд, внеурочные и неаудиторные занятия.
Как уже говорилось, работу строим в классе по технологии «Педагогических мастерских» где учитель мастер, а ученик-творец, и обязательно должен поступить запрос на ту или иную работу, что наиболее актуально на неаудиторных и дополнительных занятиях при подготовке решения заданий повышенной сложности. Ведь, как известно, то, что делается с желанием и приносит результат.
На этих занятиях присутствует право выбора, нет оценивания, дети чувствуют себя свободно, не стесняются признаться в том, что задание для них непосильно, и не стесняются обратиться за помощью к учителю и к одноклассникам (это «служба взаимопомощи», применяется игра «Учитель-ученик»). Работает «ситуация успеха», есть возможность самостоятельно проверить и оценить свои возможности, присутствуют соревновательный дух, что является движущей силой для преодоления трудностей.
К таким занятиям требуется тщательная подготовка. Проанализировав задания прошлых лет, учитывая запросы, поступившие от детей, планируем занятие. Работу строим по следующему плану:
1) знакомство с заданием (внимательно ознакомиться);
2) самостоятельное осмысливание задания, поиск путей решения;
3) озвучивание полученных результатов;
4) поиск наиболее рациональных способов решения;
5) повторение и осознание наиболее рационального способа решения;
6) первичное закрепление (решение подобного задания учеником у доски);
7) работа по карточкам, где от собственной оценки зависит выбор и количество заданий.
Самое сложное для детей понять, что нужно сделать сразу после прочтения задания. Учитель, который хочет развить самостоятельность в логическом мышлении, должен действовать следующим образом:
1) Задать вопросы для начала дискуссии:
– С чего начнем?
– Ребята, кто знает, что нужно делать?
– Какие предложения есть по решению задачи?;
2) Фиксировать предлагаемые варианты на доске или в отдельном журнале;
3) Провести голосование в пользу одного из вариантов, которым должен
воспользоваться каждый ученик при самостоятельном решении
4) Узнать, какие ответы получились в итоге
5) Попросить одного из учеников продемонстрировать решение подробно.
6) Обсудить, если возникали ошибки, то с чем связаны, на каком этапе были допущены.
7) Демонстрировать связь математических операций с жизнью, чтобы ученики понимали, где им пригодятся знания.
Как ведётся работа, можно показать на примере задания № 12 (Тренировочная работа № 7) Авторы Волкова и Бубнова
Задание № 12
Шнур длиной 32 метра складывают пополам и разрезают в месте сгиба. Каждый из полученных кусков снова складывают пополам и разрезают. Так делают до тех пор, пока не получат отрезки длиной 2 метра. Сколько раз придётся повторить эту операцию? (15 раз)
Чтобы был результат, конечно же, нужно закрепление. Для этого подготавливаем карточки с заданиями. Предлагается три задания на решение определённого типа, два из них обязательны, а одно на усмотрение ребёнка — хорошо усвоил материал — можешь остановиться и стать «учителем», есть затруднения — обратись за помощью к педагогу, либо «учителю- ученику» или можешь отдохнуть в зоне отдыха. Дети работают самостоятельно, а учитель имеет возможность поработать индивидуально с детьми, которые нуждаются в помощи или которые могут справиться с заданиями более сложного уровня
Карточка с дополнительными заданиями
- Шнур длиной 48 метров складывают пополам и разрезают в месте сгиба. Каждый из полученных кусков снова складывают пополам и разрезают. Так делают до тех пор, пока не получат отрезки длиной 3 метра. Сколько раз придётся повторить эту операцию? (15 раз)
- Кусок ткани длиной 24 метра складывают пополам и разрезают в месте сгиба. Каждый из полученных кусков снова складывают пополам и разрезают. Так делают до тех пор, пока не получат отрезки длиной 3 метра. Сколько раз придётся повторить эту операцию? (7 раз)
- Кабель для Интернета длиной 84 метра складывают пополам и разрезают в месте сгиба. Каждый из полученных кусков снова складывают пополам и разрезают. Так делают до тех пор, пока не получат отрезки длиной 3 метра. Сколько раз придётся повторить эту операцию? (31 раз)
Но, как уже было сказано, работа по подготовке к ВПР ведётся не только на дополнительных занятиях, но и на уроках присутствуют элементы. Учебный материал уроков математики особенно удобен для развития логического мышления. На основе заданий повышенной сложности составила банк тренировочных заданий, которые ежедневно включаю в уроки на орфографических пятиминутках, устном счете, на обобщающих уроках, да и при выполнении всех заданий обсуждаем с детьми, как составлено задание, в чем его особенность, какой планируемый результат оценивается. Таким образом, на уроке учащиеся должны:
У — узнавать новое, удивляться интересному
Р — развивать вычислительные навыки, рассуждать
О — обсуждать выполненные задания, открывать неизученное
К — корректировать свои знания
На моих уроках присутствуют задания на развитие всех логических приёмов мышления. Рассмотрим примеры таких заданий. Логические задачи позволяют эффективно развивать: внимание, воображение, фантазию, образное и понятийное мышление, зрительную, слуховую и смысловую память, что благополучно сказывается на усвоении программного материала.
Логические задачи позволяют эффективно развивать: внимание, воображение, фантазию, образное и понятийное мышление, зрительную, слуховую и смысловую память, что благополучно сказывается на усвоении программного материала.
Примеры заданий на логику по математике
Все эти задания не дают возможности угадывания правильного ответа, заставляют школьников размышлять, обдумывать свои действия. Поэтому они носят исследовательский характер, активизирую мыслительные способности, учат находить наиболее рациональные способы решения, одним словом заставляют мыслить логически.
Анализ и синтез.
– Прочитай по-разному выражение 16–5 (16 уменьшили на 5; разность чисел 16 и 5; из 16 вычесть 5).
– Прочитай по-разному равенство 15–5 = 10 (15 уменьшить на 5, получим 10; 15 больше 10 на 5; разность чисел 15 и 5 равна 10; 15 — уменьшаемое, 5 — вычитаемое, 10 — разность; если к разности (10) прибавить вычитаемое (5), то получим уменьшаемое (15); число 5 меньше 15 на 10).
Как по-разному можно назвать квадрат? (Прямоугольник, четырёхугольник, многоугольник.)
Расскажи всё, что ты знаешь о числе 325. (Это трёхзначное число. Оно записано цифрами 3, 2, 5; в нём 325 единиц, 32 десятка, 3 сотни. Его можно записать в виде суммы разрядных слагаемых так: 300+20+5. Оно на 1 единицу больше 324 и на 1 единицу меньше числа 326. Его можно представить в виде суммы двух слагаемых, трёх, четырёх и т. д.)
Задания на выявление различных закономерностей (правил).
Например:
1. По каким признакам можно разложить пуговицы в две коробки?
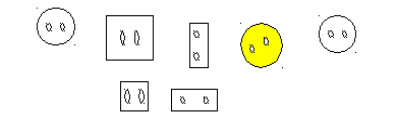
2. разгадай правило, по которому составлена таблица, и заполни пропущенные клетки:
|
4 |
6 |
9 |
3 |
8 |
6 |
5 |
2 | ||
|
5 |
7 |
8 |
2 |
4 |
6 |
Задания с геометрическим материалом.
Сколько отрезков на данном чертеже? Сколько треугольников? Сколько многоугольников?
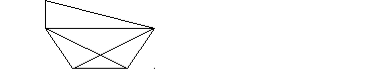
Вариативные задания.
Запиши все чётные числа от 2 до 20 и все нечётные числа от 1 до 19.
2 4 6 8 10 12 14 16 18 20
1 3 5 7 9 11 13 15 17 19
Придумайте задания к этим рядам.
— Разбей числа каждого ряда на две группы так, чтобы в каждой были числа похожие между собой.
— По какому правилу составлен первый (второй) ряд? Продолжи его.
— Какие числа нужно вычеркнуть в первом ряду, чтобы каждое следующее было на 4 больше предыдущего.
— Подбери из первого ряда пары чисел, разность которых равна 10. (из второго)
— Какая пара лишняя?
Приём сравнения.
Назови признаки:
а) выражения 3 + 2 (числа 3 и 2, знак «+»)
б) равенства х + 5 = 9 (х — неизвестное число, числа 5 и 9, знаки «=», «+».)
В чём сходство и различие:
а) выражений: 6 + 2 и 6–2;
б) чисел: 32 и 45, 1 и 11, 32 и 23 и т. д.
в) равенств: 4 + 5 = 9 и 5 + 4 = 9;
г) текстов задач;
д) геометрических фигур:

е) уравнений: 3 + х = 5 и х + 3 =5; 10 — х = 6 и (7 + 3) — х = 6;
ж) вычислительных приёмов: 9 + 6 = 9 + (5 + 1) = 15 и 19 + 16 = 19 + (10 +6) = 35.
Убери лишний предмет…
Расположи числа в порядке возрастания: 12, 9, 7, 15, 24, 2.
Продолжи ряды чисел: 2, 4, 6, …; 1, 5, 9, 13,….
Приём классификации.
Разбейте данные числа на две группы, чтобы в каждой оказались похожие числа: 33, 84, 75, 22, 13, 11, 44, 53; 91, 81, 82, 95, 87, 94, 85.
Разбейте данные выражения на группы по какому-то признаку: 3 + 1, 4–1, 5 + 1, 6–1, 7 + 1, 8–1.
Убери лишнюю фигуру.

Чем похожи все другие фигуры? Как их можно назвать?
Приём аналогии.
– Изучение письменного сложения трёхзначных чисел по аналогии с двузначными числами.
– Изучение переместительного свойства умножения по аналогии с переместительным свойством сложения.
– Изучение нумерации чисел.
Приём обобщения
Сравни выражения, найди общее в полученных неравенствах, сделай вывод:
2 + 3 … 2 * 3 4 + 5 … 4 * 5
Найди сумму. Сравни её с каждым слагаемым. Сделай соответствующий вывод.
|
слагаемое |
1 |
2 |
3 |
4 |
5 |
6 |
|
слагаемое |
4 |
4 |
4 |
4 |
4 |
4 |
|
сумма | ||||||
Устный счёт (зрительный и слуховой)
Математические игры: «Магический квадрат», «Индивидуальное лото», «Числовая мельница», «Кто быстрей?» и другие
Особое место нужно отвести задачам.
Решение нестандартной задачи. Дети сами приходят к выводу, что есть задачи, которые не решаются сразу одним действием, что надо анализировать, сравнивать, рассуждать.
Решение задач с недостающими данными способствуют развитию нешаблонного анализа. (Задача: Мальчику купили игрушки: мишку и машину. Машина стоит 25 рублей. Сколько стоят вместе?).
Нерешаемые задачи (Задача: У Кати было 5 кукол, у Светы — 1 кукла. Сколько было кукол у Веры?). Развивается умение осуществлять анализ новой ситуации.
Задачи на определение закономерности (Задача: Вставь пропущенное число 2,5,8,11,…). Решение таких задач требует умения самостоятельно осуществлять анализ ситуации и формировать гипотезы преобразования данной ситуации).
Задачи на формирование умения проводить рассуждения (Задача: Гитара — музыкальный инструмент. У Ивана дома музыкальный инструмент. Значит у него дома гитара?). При решении таких задач учащиеся должны проводить смекалку, догадаться, что задача не решается, что есть лишние данные или данных не хватает. Формируется гибкость мышления, которая играет роль в развитии творческого мышления.
Задачи-шутки используется при формировании гибкости ума, освобождает мышление от шаблонов. Такие задачи не привязаны к темам и не требуют особой теоретической подготовки. (Задачи: Сколько концов у двух палок, у трёх палок, у пяти палок, у пяти с половиной палок?).
Задачи на переливание формируют математический стиль решения.
(В первый сосуд входит 10 литров воды. Как используя ещё два пустых сосуда по 5 и 8 литров, разделить воду на две части?)
Моделированные ситуации с помощью чертежа или рисунка (Задача: Вася выше Коли и ниже, чем Соня. Кто из мальчиков самый длинный?). При решении таких задач желательно сопроводить сюжет рисунком.
Особо хочу остановиться на работе, при подготовке к ВПР, во время внеурочной деятельности на кружке «Логика», который я веду четвёртый год. Цель данного курса: развитие познавательных способностей учащихся на основе системы развивающих занятий. При подготовке занятий пользуюсь методиками С. Гин и О.Холодовой. Дети учатся мыслить логически, находят решения нестандартных задач и выход из различных ситуаций, учатся анализировать поступки и высказывают собственное мнение, что конечно же сказывается на дальнейшем поведении и работе детей.
На этих занятиях уже ведётся систематическая работа по подготовке к решению заданий повышенной сложности.
Развивающий курс внеурочной деятельности «Логика»
Основная цель курса: развитие интеллектуально-творческого потенциала личности ребёнка.
- В соответствии с целью определены конкретные задачи курса:
- Развитие познавательных способностей младшего школьника.
- Развитие его творческих способностей.
- Расширение кругозора учащихся.
- Развитие эмоционально-волевой сферы.
- Формирование стремления ребёнка к личностному росту.
Особенности занятий по курсу внеурочной деятельности «Логика» принципиально отличаются от школьных уроков тем, что ребёнку предлагаются задания не учебного характера. Основное время на занятиях отведено самостоятельному выполнению детьми логически-поисковых заданий, благодаря этому у детей формируются общеучебные умения: действовать самостоятельно, принимать решения. И если в начале работы по данному курсу выполнение многих предложенных заданий вызывает у детей трудности, так как на традиционных уроках они не встречались с заданиями такого типа, то к концу курса большинство учащихся должны справляться с большим числом заданий.
Задания на развитие внимания. Кзаданиям этой группы относится ряд упражнений, направленных на развитие произвольного внимания, его объёма и устойчивости, переключения и распределения. Выполнение заданий подобного типа способствует формированию умения целенаправленно сосредотачиваться, вести поиск нужного пути, находить самый короткий путь решения задач. Например, «Поиск одинаковых предметов», «Что изменилось», «Какого предмета не хватает», «Найди отличия», и другие .
Задания, развивающие слуховую и зрительную память. Например, «Сокращение», «Определи игрушки», «Поиск предмета по заданным признакам», «Простукивание».
Задания на развитие и совершенствование воображения
«Определения», «Способы применения предмета», «Поиск аналогов» «Заглавие», «Исключение лишнего слова».
Задания, направленные на развитие мышления
«Задача Ломанная кривая»,«Определения», «Дорисуй фигуры», «Соедини буквы».
Формы работы
– предметные декады (занимательные занятия, КВН по предметам);
– олимпиады по предметам;
– конкурсы творческих работ;
– игры-соревнования;
– интеллектуальный марафон.
Таким образом, принципиальной задачей предлагаемого курса является именно развитие познавательных способностей и общеучебных умений и навыков, а неусвоение каких-то конкретных знаний и умений.

