В статье проводится сравнение скорости вычисления функции sin() для разных типов данных. Результаты статьи можно учитывать при разработке учебных или производственных проектов, в которых используются тригонометрические вычисления. В частности, рассматривается случай трассировки лучей в компьютерной графике.
Ключевые слова: си, тригонометрическая функция, бенчмарк, компьютерная графика.
Введение.
Графические технологии глубоко проникают в повседневность людей. Сейчас сложно представить человека, который не играл бы в компьютерные игры или не смотрел бы кино про супергероев. Во всех этих вещах присутствует компьютерная графика, которую разрабатывают программисты.
Одним из методов представления изображения на мониторе является рейтрейсинг (англ. ray tracing) [1]. Суть его заключается в том, что из точки наблюдения (обычно её называют камерой) “бросаются” лучи в точку, которую должен видеть наблюдатель. По мере “полёта”, луч встречает на своём пути различные объекты, которые имеют какую-то текстуру, как-то освещены и т. п. Как только луч завершает свой “полёт” в видимой ячейке (обычно пиксель экрана) отображается необходимый цвет . “Бросив” луч нужное количество раз в нужные места можно сформировать целостную картину того, что предполагалось отобразить.
Ясно, что для картинки в FullHD разрешении (1920 * 1080 пикселей) такой бросок луча необходимо выполнить более двух миллионов раз! Это довольно много, поэтому разумно задуматься над инструментами и методами, с помощью которых будет выполняться расчёт “броска” луча.
В алгоритме “броска” луча необходимо использование тригонометрических функций [2]. Например, при расчёте угла, на который необходимо сместить луч при переходе к следующему пикселю, или если необходимо рассчитать угол, под которым луч отражается (или преломляется) при переходе через полупрозрачный объект.
Сам угол в программе можно хранить в разных типах данных.
Скорость работы тригонометрических функций с использованием разных типов данных и будет рассмотрено в данной статье.
Среда и объект исследования.
Для чистоты эксперимента, в качестве языка программирования будем использовать чистый Си. Это позволит максимально сократить издержки [3, 4] более высокоуровневых языков программирования (python, java).
Для тестирования будем использовать встроенные типы double и float. Это связано с тем, что любые производные типы будут так или иначе основаны на работе с этими базовыми типами. Также создадим таблицу заранее рассчитанных sin(), которая будет хранить double значения конкретного угла.
Тестировать будем стандартную функцию библиотеки Си sin() (sinf() для float, получение значения из таблицы, для таблицы sin()) из math.h.
Компилятор:
Apple clang version 11.0.0 (clang-1100.0.33.17)
Target: x86_64-apple-darwin18.7.0
Thread model: posix
Флаги компиляции:
-Wall -Wextra -Werror
Рабочая станция:
Processor: 3 GHz Intel Core i5
Memory: 8 GB 2667 MHz DDR4
Код программы:
См. приложение или в git репозитории автора: https://github.com/vesord/estimation_of_the_speed_of_trigonometric_functions
Методика расчёта.
1. Сгенерируем случайную последовательность углов.
Причем, для каждого теста (тип float, таблица) проведём необходимую конвертацию типов заранее (массив углов для double останется без изменений; массив углов для float сформируется из массива double приведением типов; массив углов для таблицы будет представлять целочисленный массив, содержащий индексы значений, которые необходимо получить). Предполагаем, что в программе, которая использует таблицу синусов существует своя система типов, и при вызове функции sin_from_table() не будет происходит дополнительных конвертаций типов.
2. Для каждого теста рассчитаем синус угла, для каждого значения угла, подготовленного на шаге 1.
Важно, что результат вычислений накапливается в переменной tmp. Это необходимо для того, чтобы компилятор при оптимизации нашего кода не отбросил “ненужные” операции.
3. Повторим тест (шаги 1–2) для таблицы, сгенерированной с другим random seed.
Тест для значений float отличается от тестов для double и таблицы, поскольку в нем происходит суммирование значений float вместо double. Это делает результат для float немного быстрее, однако не настолько, чтобы сильно повлиять на результат теста. При получении данных из таблицы происходит обращение к памяти, а при вычислении синуса происходит вычисление серии Фурье или полиномов Чебышева [5]. Эти операции выполняются в разы дольше, чем разница по времени сложений float и double чисел.
Результаты.
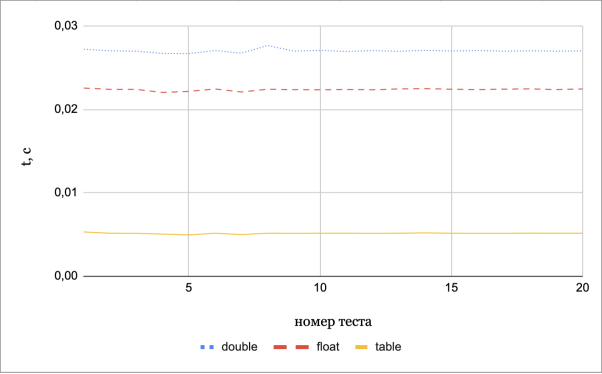
Результат сравнения трёх способов получения sin() представлен в таблице 1.
Таблица 1
Сравнение скоростей получения значений sin() .
Вывод.
Несмотря на необходимость рассчитывать таблицы тригонометрических функций перед их использованием, они являются гораздо более быстрым (в 5 раз быстрее для синуса) способом вычисления необходимого значения. Целесообразно учитывать скорость расчёта синуса при разработке учебных или профессиональных проектов, использующих эти математические функции.
Приложение.
В приложении приведен код заполнения массивов со случайными углами и функция теста для типа double. По ним можно получить представление о том, как проводилось исследование. Полный текст программы можно найти в github репозитории автора.
void rand_fill_angle_table(double *table_d, float *table_f,
size_t* table_t, size_t table_t_size, size_t size)
{
double angle_steps;
double angle_step = 2. * M_PI / table_t_size;
int divisor;
for (size_t i = 0; i < size; ++i)
{
divisor = rand();
divisor = divisor == 0 ? 1 : divisor;
table_d[i] = (double)rand() / (double)divisor;
table_f[i] = (float)table_d[i];
modf(table_d[i] / angle_step, &angle_steps);
table_t[i] = (int)angle_steps % table_t_size;
}
}
void test_sin_double(double *angle_table, size_t size)
{
clock_t start, stop;
double tmp = 0;
start = clock();
for (size_t i = 0; i < size ; ++i)
{
tmp += sin(angle_table[i]);
}
stop = clock();
printf("%10f", (double)(stop - start) / (double)( CLOCKS_PER_SEC ));
Литература:
- Трассировка лучей. — Текст: электронный // Википедия свободная энциклопедия. — URL: https://ru.wikipedia.org/wiki/Трассировка_лучей (дата обращения 14.11.2020)
- Городничев М. Г. О некоторых методах визуализации динамических 3D моделей. / М. Г. Годродничев, Р. А. Гематудинов, А. М. Кухаренко // Экономика и качество систем связи. — 2018. — URL: https://cyberleninka.ru/article/n/o-nekotoryh-metodah-vizualizatsii-dinamicheskih-3d-modeley/viewer (дата обращения 10.11.2020)
- Цилюрик О. Производительность языков программирования. — Текст: электронный. -URL: https://www.ibm.com/developerworks/ru/library/ManySpeed_08_1/index.html (дата обращения 12.11.2020)
- Тесты простейших приложений на различных языках программирования. — Текст: электронный. — URL: https://www.opennet.ru/opennews/art.shtml?num=51992 (дата обращения 12.11.2020)
- Hart J. F. Computer Approximations. / J. F. Hart, E. W. Cheney, C. L. Lawson, H. J. Maehly, C. K. Mesztenyi, J. R. Rice, H. C. Thacher, C. Witzgall Computer Approximations // — R. E. Krieger Publishing Company. — 1978.







