Элективный курс «Фракталы». Вводный урок



Тема урока: Фрактал — это…

Тип урока: открытие нового знания.

Форма урока: урок-лекция.

Цель урока: дать понятие фрактального множества, обсудить его свойства на понятных примерах.

Задачи урока:

1. познакомиться с фракталами, свойствами фрактальных множеств;
2. привить интерес к углубленному изучению информатики;
3. развить пространственное воображение.

Прогнозируемые результаты:

Предметные

— Формирование знаний о фракталах;

— Формирование информационной и алгоритмической культуры.

Метапредметные

— способность принимать и сохранять цели и задачи учебной деятельности, находить способы её осуществления;

— умение планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её выполнения;

— умение включаться в диалог с учителем и сверстниками, в коллективное обсуждение проблем;

— умение оценивать себя и результаты своей работы.

Оборудование: персональный компьютер (ПК) учителя, мультимедийный проектор, экран, видео.

Ход урока

I . Мотивационно- целевой этап

1. Организация учащихся на урок

2. Определение темы и цели урока

Наш курс называется «Фракталы». Сегодня у нас вводный урок «Фрактал — это …»

— Как вы думаете, какая цель перед нами сегодня стоит? ( познакомиться с понятием фрактал, рассмотреть его свойства )

— Кто-нибудь знает, что такое фрактал?

— Фрактал — геометрический объект, в котором один и тот же фрагмент повторяется при каждом уменьшении масштаба, т. е. фигура, обладающая свойством самоподобия.

3. Актуализация знаний

— Давайте, вспомним из курса геометрии, что такое подобие, какими свойствами оно обладает.

Преобразование подобия — это преобразование, при котором расстояние между любыми двумя точками изменяется в одно и то же число раз. Это число называется коэффициентом подобия k . k > 0

Свойства:

— Преобразование подобия сохраняет порядок точек на прямой.

— Точки, не лежащие на одной прямой, при преобразовании подобия переходят в точки, не лежащие на одной прямой.

— Преобразование подобия переводит прямую в прямую, отрезок в отрезок, луч в луч, угол в угол, окружность в окружность.

— При преобразовании подобия углы сохраняют свою величину.

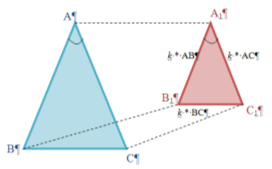
Рис. 1. Подобие

Рис. 2. Примеры геометрических фракталов [3]

Мы будем строить геометрические фракталы и немного позже разберем, как строить фрактал Коха.

4. Обеспечение мотивации познавательной деятельности учащихся .

Давайте подумаем, встречаем ли мы фракталы в вашей повседневной жизни?

На самом деле объекты, похожие на фракталы, находятся вокруг нас. Это крона деревьев, узоры на замершем стекле, облака, листья папоротника, линия морского берега, система кровообращения и т. д.

II . Процессуально- познавательный этап

1. Сообщение учителем справочного материала

Фрактал — геометрический объект, в котором один и тот же фрагмент повторяется при каждом уменьшении масштаба.

Бенуа Мандельброт образовал понятие «Фрактал» от латинского причастия fractus (ломать, разламывать). Он ввел определение фрактала как множества, которое имеет фрактальную размерность, большую топологической. Чуть позже вернемся к размерности фрактала.

Свойства фрактального F множества:

— F имеет тонкую структуру, т. е. содержит произвольно малые масштабы

— F слишком нерегулярное, чтобы быть описанным на традиционном геометрическом языке

— F имеет некоторую форму самоподобия, допуская приближенную или статическую

— в большинстве случаев F определяется очень просто, например, рекурсивно.

— обычно фрактальная размерность множества F больше, чем его топологическая размерность

2. Физминутка

3. Продолжение изучения темы

Фрактальная размерность

Рассмотрим размерность 1 .

Отрезок разобьем на n частей. Длина отрезка 1. Длина одной части . Количество частей

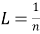
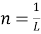
Рассмотрим размерность 2.

Возьмем квадрат со стороной 1. Разобьем на n частей. Длина стороны одной части L . Количество квадратиков

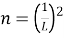
Рассмотрим размерность 3.

Возьмем куб со стороной 1. Разделим на n кубиков со стороной L. Количество кубиков

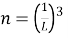
Общая формула:

, где d размерность пространства.

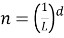
Рассмотрим построение фрактала Коха.

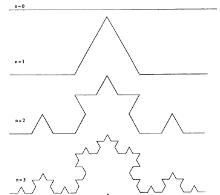
Рис. 3. Кривая Коха

Берем единичный отрезок. Делим его на 3 равные части. Убираем среднюю часть.

Вместо убранной части достраивает стороны равностороннего треугольника

Повторяем это с каждым отрезком.

Количество отрезков n после первой итерации равно 4. Длина каждого отрезка L= 1/3. Кривая Коха имеет фрактальную размерность d = 1,2618…

Размерность больше, чем размерность прямой, но меньше, чем размерность плоскости. Т. е. кривая Коха не линия и не плоскость, а что-то между ними.

4. Обобщение знаний по теме

— Давайте повторим то, что мы с вами сегодня изучили.

— Что такое фрактал?

— Назовите свойства фрактального множества.

— Как найти фрактальную размерность

III . Рефлексивно-оценочный этап

1. Подведение итога урока

— Какую цель урока мы поставили в начале? Как мы ее достигли?

— Вам было легко или были трудности?

— Что вызвало затруднения?

2.Информация о выполнении домашнего задания

Найти информацию, где применяются фракталы. На следующем занятие мы с вами это обсудим.

3. Рефлексия учебной деятельности

Анкетирование:

На занятии я работал (активно/ пассивно)

Своей работой я (доволен/ не доволен)

За занятие я (не устал/ устал)

Поставленной цели (достиг/ не достиг)

Моё настроение (стало лучше/ не изменилось)

4. Оценка содержательного аспекта деятельности учащихся на уроке (поощрение детей, выставление отметок за урок, их комментирование, замечания учащимся)

Литература:

1. Морозов А. Д. Введение в теорию фракталов / А. Д. Морозов — Москва-Ижевск: Институт компьютерных исследований, 2002. — 160 с.
2. Fractal. (2017) Fractal Zoom (Last Lights On) Mandelbrot [анимация] // YouTube. 1июня.
3. (https://www.youtube.com/watch?v=7mLl73RI2hY&feature=emb_logo)