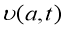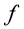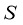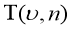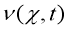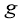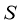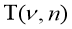Целью настоящей работы является построение математической модели землетрясений, и разработать численный метод решения обратной задачи, построить алгоритм решения поставленной задачи.
Ключевые слова: математическая модель землетрясений, уравнение сейсмики, источники данных, обратная задача, численный, конечно-разностный метод, алгоритм решения, анализ методов.
Одним из стихийных бедствий человечества является землетрясение, и оно происходит ежедневно — ощутимое и неощутимое [1, 2], и происходит около 3000 раз в день [3].
Задачи возникновения землетрясений до сих пор остается не решенной, хотя с этой проблемой занимаются многие ведущие ученые мира, проводят исследования со всеми возможностями и техниками, аппаратурами, приборами, даже животными и природными явлениями.
Активность землетрясений связана с сейсмоактивными молодыми, горными массивами на территории Кыргызской Республики, и для изучения их существует единая служба сейсмических наблюдений, состоящая из многих сейсмостанций.
На активных участках Юге Кыргызстана также расположены сейсмические станции — ЕССН, которые ведут записи магнитуды сейсмического процесса, параметры земной среды при ощущении амплитуды землетрясения.
Известно, что Центральная Азия находится под угрозой землетрясения и задачи возникновения землетрясений и их решения до сих пор остаются не доконца решенными и этим занимаются многие ведущие ученые [4].
Постановка задачи. Процесс природного явления — землетрясение описывается уравнением сейсмики. Рассмотрим обратную задачу сейсмики следующего вида [5]:
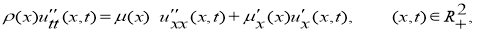
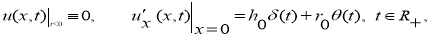
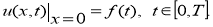
где
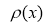
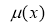
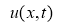
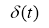
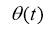
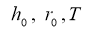
Обратная задача заключается в определении функции
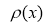
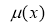
Решение. Обратная задача (1)-(3) с применением методов выпрямления характеристик и выделения особенностей приведена к обратной задаче с данными на характеристиках, и последняя задача решена численным конечно-разностным методом, затем решена первоначальная обратная задача (1)-(3).
Смещения от сейсмического источника предоставляет с собой функция Грина динамической теории упругости [6].
Пусть единичный пульс приложен в точке
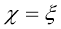
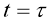
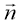
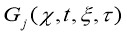

А математическая модель смещения почвы при землетрясении задается уравнением [7]:
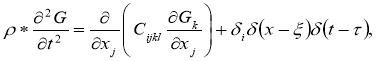
гдеρ — плотность среды.
Чтоб однозначно определить решение уравнения (1) необходимо должны задавать начальные и граничные условия.
Когда граничные условия не зависят от времени, то граничные условия записываются в виде:
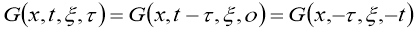
Конечно, практическое вычисление функции
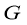
Рассмотрим в упругом теле объемом
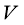
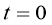
Таблица 1
Два поля смещений при начальных условиях
|
№ п / п |
Поля смещения |
Объемные силы |
Граничные условия |
Напряжение на поверхностях |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
Пусть существует момент времени t
0
, до которого
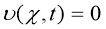
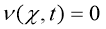
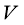
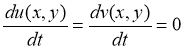
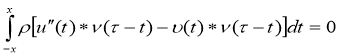
Пусть поле смещения u(х,t) удовлетворяют условию
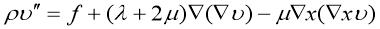
х,μ — коэффициенты Ламэ, f — сила,

Тогда существует потенциалы
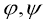
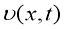
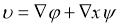
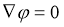
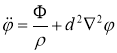
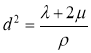
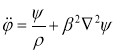
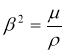
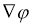
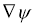
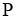
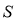
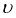
В изотропной среде упругие модули остается только
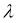
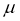
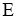
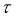
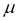
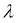
Приводим зависимости модулей для изотропной среды:
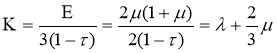
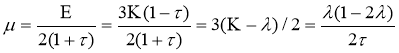
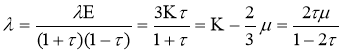
где
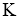
Между дилатацией
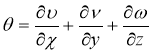
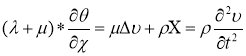
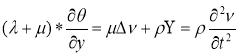
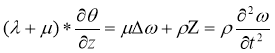
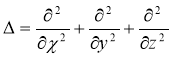
Отсутствие внешних сил следует X=Y=Z=0, а составляющие вектора
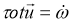
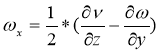
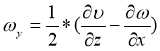
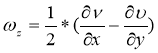
тогда из (10) — (12) следует два уравнения
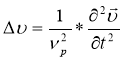
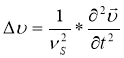
Уравнение (15) — (16) являются волновыми уравнениями и описывают распространения продольных и поперечных волн соответственно, скорости определяются по формулами:
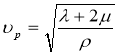
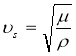
Отметим, что
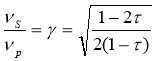
В совокупности продольные и поперечные волны называют объемными волнами.
Заключение. Землетрясения, как следует из вышенаписанных, приносят человечеству огромный ущерб, вред, жертвы, это означает необходимо изучать их и информацию о них.
Материальный ущерб от землетрясения в Кыргызстане составляет, за последние 15 лет, составляет около 105 млн.$, а землетрясения в большинство случаях происходят в Кыргызстане, где проживают 51 % населения Кыргызстана.
Это означает актуальность, необходимость изучения землетрясений Кыргызстана.
С точки зрения практики авторы считают, что наиболее приемлемым методом решения этих задач является, конечно-разностный метод. В этом случае, конечно, необходимо установить устойчивость решения, т. е. уравнение движения идеально упругой изотропной среды (13) — (15) можно записать в виде [8,9]:
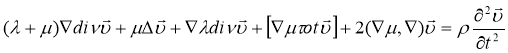
где
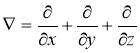
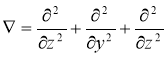
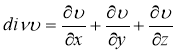
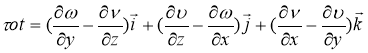
Уравнение (21) в однородной среде имеет вид
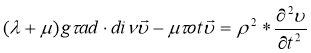
где
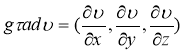
Из уравнения движения однородной среды (22) в некоторых упрощениях можно получить уравнение сейсмических волн в двумерном случае, т. е. уравнение зависит от двух пространственных переменных,
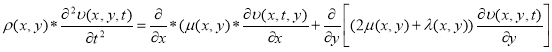
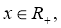
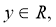
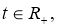
Для задания начальных и граничных условий рассмотрим широко распространенная в геофизике модель среды, состоящих из двух полупространств x>0 и x<0 и с границей на плоскости x=0. Здесь предположим, что коэффициенты Ламэ и плотность среды гладки в этих полупространствах и имеет конечный скачок при переходе из одного полупространства в другое полупространства.
В статье разработана математическая модель волновых процессов землетрясений и получена уравнение сейсмики, составлены также начальные и граничные условия задачи, учитывающие особенности сейсмических волн Юга Кыргызстана. А также более подробно приведены численные методы решения прямых и обратных задач сейсмических волн, и они проанализированы.
Литература:
- Потапов А. Д., Ревелис И. Л., Чернышев С. Н. Землетрясения. Причины, последствия и обеспечение безопасности. М.: Инфра-М, 2017. — С.344.
- Никонов А. А. Землетрясение. М.: Знание. 1984. — С.192.
- Уломов В. И. Динамика Земной коры Средней Азии и прогноз землетрясений. Ташкент: ФАН. 1974. — С.218.
- Аки И., Ричардс П. Количественная сейсмология. — М.: Мир. 1983. — С.520.
- Сатыбаев А.Дж., Алимканов А. А., Култаев Т. Ч. Алгоритм определение одной обратной задачи сейсмики с мгновенным и шнуровым источниками. Бишкек: Известия КГТУ им. И.Раззакова. 2016, № 3 (39), часть I. с. 175–180.
- Романов В. Г. Обратные задачи математической физики. — М.: Наука, 1984г. — 264 с.
- Сатыбаев А.Дж. Численное определение коэффициента Ламэ в уравнении сейсмики //История, культура и экономика, наука юга Кыргызстана. — Ош: КУУ, 2000.- С.148–152.
- Кабанихин С. И. Обратные и некорректные задачи. Новосибирск: Сибирское научное издательство. 2009г. — 457с.
- Яхно В. Г. Обратные задачи для дифференциальных уравнений упругости. Новосибирск: Наука, Сибирское отделение, 1990г. — 304 с.