Для осуществления контроля энергосистемы и реализации релейной защиты на питающей линии тяговой сети постоянного тока устанавливаются устройства измерения тока питающей линии. Информация о токе в цепи формируется датчиком тока в аналоговой форме и преобразуется в цифровой вид с помощью 8-битного аналого-цифрового преобразователя (АЦП) с параллельным двоичным выходом.
При манипуляции данными необходимо производить различные операции, такие как: проверка попадания числа в промежуток значений, сравнение числа с некоторым значением, в том числе проверку на кратность значений тока. Такие операции для быстродействия следует выполнять не через перевод к 10-й системе счисления и последующим делением на вычислительных машинах, а реализовывать на дискретных устройствах.
В данной статье будут рассмотрены методы проверки положительных целочисленных значений на кратность от 2 до 9. Для реализации используется виртуальная лаборатория Matlab/Simulink.
Принцип деления на числа равные 2 k основывается на правилах перехода от 2-ой к 10-ой системе.
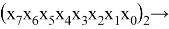
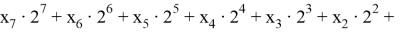
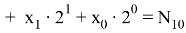
Очевидно, что число N будет делится на
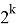
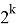
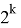
Кратность 2
Исходя из выше сказанного, очевидно, что для проверки на кратность 2 из битого выражения числа необходимо извлечь нулевой бит и исследовать его содержимое. Если его значение равно 0, то в алгебраической сумме не будет 1
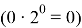
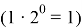
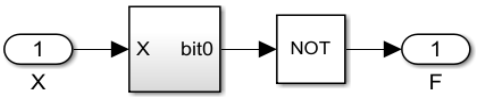
Рис. 1. Реализация модуля проверки числа на кратность 2
Кратность 3
Для определения кратности 3 число необходимо разбить на две группы: чётные и нечётные позиции битов. Последовательно сложить между собой все биты каждой группы. Затем, из суммы чётных битов вычесть сумму нечётных битов и проверить эту разность на наличие 00 или 11 2 (3 10 ).
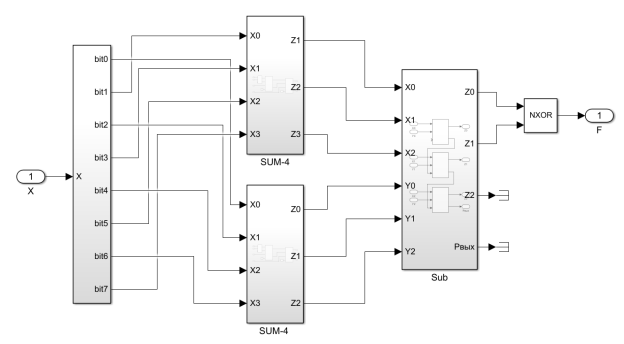
Рис. 2. Реализация модуля проверки числа на кратность 3
Кратность 4
Для проверки на кратность 4 из битого выражения числа необходимо извлечь нулевой и первый биты. Они отвечают за наличие в сумме 1 и 2, соответственно. Если значение 0 бита равно 0, то в алгебраической сумме не будет 1
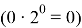
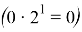
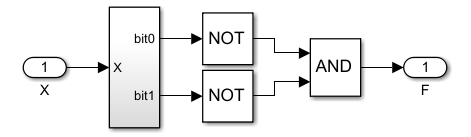
Рис. 3. Реализация модуля проверки числа на кратность 4
Кратность 5
Для определения кратности 5 число необходимо разбить на группы по 2 бита. Сложить между собой все группы на четных и на нечетных позициях отдельно. Из суммы чётных пар вычесть сумму нечётных пар и проверить эту разность на наличие 000 или 101 2 (5 10 ).
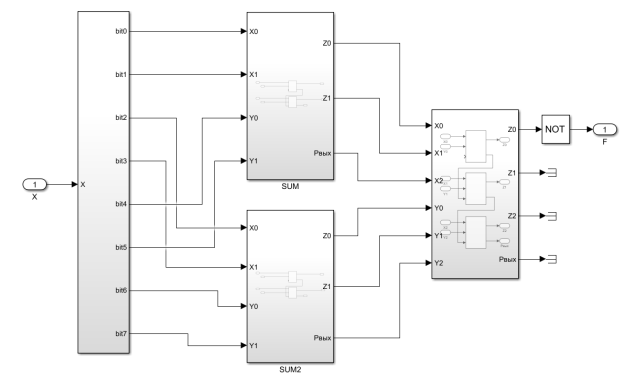
Рис. 4. Реализация модуля проверки числа на кратность 5
Кратность 6
Для определения кратности 6 следует проверять число и на кратность 2, и на кратность 3 одновременно, используя принципы, изложенные ранее.
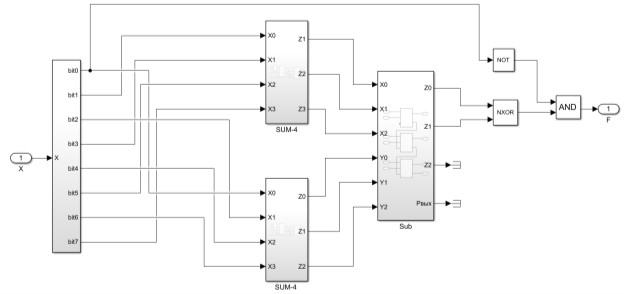
Рис. 5. Реализация модуля проверки числа на кратность 6
Кратность 7
Для определения кратности 7 необходимо разбить двоичную запись проверяемого числа справа налево на группы из 3-х знаков. Сложить полученные группы. Если сумма имеет больше трёх разрядов, то повторить разбиение и сложение. В случае, когда сумма равна 111 число делится на 7 без остатка, иначе — не делится.
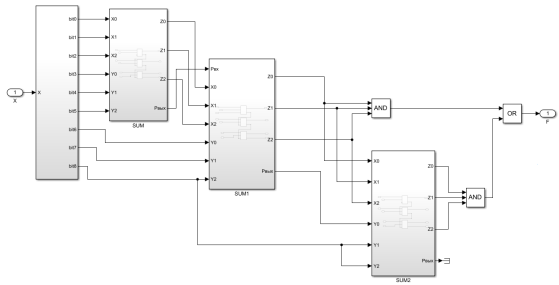
Рис. 6. Реализация модуля проверки числа на кратность 7
Кратность 8
Признак кратности на 8 схож с признаком кратности на 4, однако, необходимо проверять не только 0 и 1 биты, а ещё и 2. Если же во всех трёх битах значения будут равны 0, то число делится на 8 без остатка.
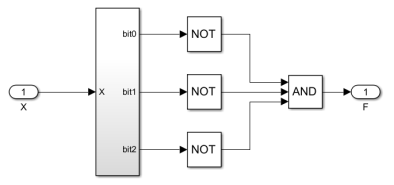
Рис. 7. Реализация модуля проверки числа на кратность 8
Кратность 9
Для проверки на кратность 9 10 (100110 2 ) разобьём 8 битов, формирующих двоичное число, на три группы по три бита, начиная с младшего разряда. Сложим нечётные группы, после вычтем их из чётных, если полученный результат будет равен 0, тогда число после искомой последовательности кратно 9.
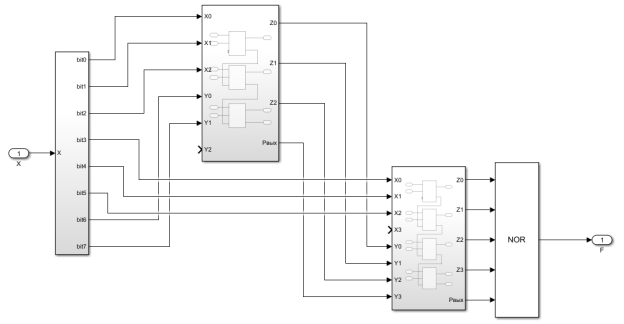
Рис. 8. Реализация модуля проверки числа на кратность 9
Вывод
Мы приходим к выводу о том, что основные методы проверки чисел на кратность заключаются в проверке наличия в битах нулей для чисел 2 k и в разбиении битов числа на группы и последующим действиям с ними.
Данная работа может помочь при разработке схем релейной защиты и систем контроля сети электроснабжения, в частности, для обеспечения надежности и ускорения аппаратной работы по анализу входных данных.
Литература:
- https://fenikso.livejournal.com/9676.html
- http://mathhelpplanet.com/viewtopic.php?f=10&t=19256&st=0&sk=t&sd=a

