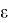In the article we use the concepts of mathematics in conducting and analyzing physics classes in secondary schools. To ensure the continuity of physics and mathematics, we must pay attention to the sequence of topics in these textbooks. The following analyzes the relevance of topics in physics and mathematics in secondary schools.
Key words: interconnection, continuity, lesson, physics, mathematics, laboratory, absolute error, relative error, systematic error, gross error, indirect, direct.
В статье анализируется использование математических понятий при проведении уроков физики в общеобразовательных школах. Утверждается, что взаимосвязь между предметами необходимо рассматривать как объективный процесс, сориентированный на целостное формирование, развитие и воспитание учащегося с учетом его познавательных способностей и возможностей. Анализируется актуальность взаимосвязи учебных тем по физике и математике в средней школе.
Ключевые слова: интеграция, физика, математика, лаборатория, абсолютная ошибка, относительная ошибка, систематическая ошибка, косвенная ошибка, прямая линия.
Introduction
As we know that, the knowledge gained through laboratory classes in physics has a significant role in its didactic properties. These opportunities should be widely used in education, especially in secondary schools. This is because all the processes taking place in nature begin to study physically. As students apply their theoretical knowledge to practice, the knowledge gained will be further strengthened. For this reason, after a certain section in physics textbooks in secondary schools, the laboratory classes related to this section will be held. In the laboratory classes, students will be able to link their theoretical knowledge to practice, further strengthen their practical skills and abilities, and increase their interest in physics. The content of lab training in physics in schools is based on measuring the values of physical quantities, studying physical phenomena and its regularities. In this lab, we are faced with deficiencies in textbooks [1–3].
First, physics textbooks do not provide information about the methods of measuring physical quantities, or «Absolute and relative errors” before conducting laboratory trainings. However, before taking lab training, students should be aware of the above sizes. The second, the concepts of absolute and relative error are used to form mathematical concepts in the 8th grade algebra textbook that addresses the topics of absolute errors and relative errors. But in the 7th grade physics class, you must identify absolute and relative errors in lab training. From these we can see that the topics of absolute errors and relative errors are not in the 8th grade algebra textbook but in Chapter 1 or 2 of the Grade 7 algebra textbook, so students do not have difficulty in identifying absolute and relative errors in measurements in the physical labs and have a high level of assimilation [3–5].
In this direction, our physical scientists K. A. Tursunmetov, U. Oltmishev, D. Begmatova, H. M. Sattorov «Mathematical processing of measuring techniques and results of educational laboratory experiments” (In general physics laboratory practicum), Begmatova, U. Oltmishev “The role of mathematics in improving the effectiveness of laboratory physics practicum” — Journal of Public Education and as well as А. М. Khudayberganov has studied such issues as “Issues of Continuity in Teaching Physics in General Secondary Schools”. However, prior to conducting laboratory studies in secondary schools, physics textbooks should include topics such as measuring physical size, absolute and relative error, and making sure that physics and mathematics are consistent. The following are some of the physical and mathematical implications of the concepts that students need to know before taking lab classes in physics.
1) The statement of the problem
Physical parameter is a quantitative characteristic of a process. Any process can be mathematically expressed using the physical quantities. Measuring physical parameters is a process of comparing it with the same homogeneous quantity. Measurements can be divided into two parts: indirect and direct measurements. If we reach the measurements that we need to measure using a measuring tool, this method is called direct or indirect measurement. For example: time, length, current, and so on. Indirect measurement is called the indirect result when a mathematical operation (indirect, division, root, logarithmic, etc.) is to be obtained by directly measuring magnitudes. When measuring any physical size many errors are made for various reasons. The error that arises from the imperfections of the measurement method or instrumentation is called a systematic error . This error can be measured by another method. An error that occurs for a variety of reasons is called a random error . For example: drastic changes in external conditions and the like. Random error reduction can only be considered because of repeated experiments [7,8].
Errors caused by the neglect of the experimenters are called gross errors. For example, measuring the wrong measurements on a scale of measuring devices or performing them incorrectly. For the above reasons, the experimentally measured magnitude is determined to some extent by the actual value. The error can be either absolute or relative. Difference between the arithmetic mean and a 0
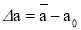
is called an absolute error. The relative error can express as a percentage of
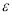
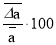
Will be here is the average value of the absolute magnitude. The Grade 8 algebra textbook provides information on absolute and relative errors [9].
2) Scientific results and their analysis
1) In most cases the exact values of quantities are unknown, so absolute error of approximation cannot be found. However, it is often possible to estimate absolute error if convergence is known.
1 — Task. The upper end of the liquid column is between 21 and 22 ° C on a room thermometer. The approximate value of the temperature is 21.5. Estimate the absolute error of convergence. The exact value of the temperature △t is unknown, but it is 21≤ t ≤22 . To estimate the difference between the exact value of the temperature and the approximate value, that is, the value of t=21.5, we subtract 21.5 from each part of this double inequality. 00.5 ≤ t ≤ 0.5 , that is | t -21.5 | Let ≤ 0.5 . Thus, the absolute error is less than 0.5. In this case, the temperature is said to be measured with accuracy up to 0.5 and is written as follows: t = 21.5 ± 0.5. Generally, if a number x is the approximate value of x and | x -a | If ≤ h , then x is equal to a number x and is written as follows:
x = a ± h (3)
| x-a | ≤ h inequality
a — h ≤ x≤a + h (4)
Note that double inequality is the same. For example, x = 2.43 ± 0.01 records that x is equal to 2.43 with a precision of 0.01, that is, 2.43–0.01 ≤ x ≤ 2.43 + 0.01 or 2.42 ≤x ≤ It is 2.44. The numbers 2.42 and 2.44 are the approximate values of x, respectively, with the same number. In measuring the temperature normally considered in the matter, the approximate value of the temperature is 21 or 22°C. In this case, the absolute error of each approximation does not exceed 1°C. Therefore, it is generally assumed that when measuring the temperature using a thermometer with sections of 1°C, the measurement is made with accuracy up to 1°C.
For other measuring instruments, the measurement accuracy is usually calculated by the smallest unit. For example, length is measured in micrometers up to 0.01 mm, temperature is measured by medical thermometer at 0.1°C, second-hand clock shows clock time in 1 second. Thus, the measurement error depends on which instrument is measured. The smaller the convergence error, the more accurate the measurement instrument. After the teacher passes the subject, they are given several examples to make sure that the students understand. For example, what does the following note mean
x = 4.9 ± 0.2; 2) x = 0.5 ± 0.15
2) The rounding of numbers is used to deal with approximate values of various sizes in many practical matters of physics, mathematics, and technology. For example, the rate of free fall of bodies at sea level and 45° is 9.80665 m/s 2 . Usually this number is rounded to one in ten: 9.8. It is written as follows: g≈ 9.8 (read: g is approximately 9.8). x ≈ a means that a number x is an approximate value.
2 — Task. The rectangular surface area is 35 m2 and 8 m high. Find the width of the field. The width of the area is l meters, then l = 35: 8 = 4,375. Answer: 4,375 m. In practice, this result is usually rounded to one-tenth, that is, ≈4,3. Let's look at the rule of rounding numbers. Require rounding 4,647 to one hundred. For rounding with Kami we omit 180 last 7 digits, resulting in 4.64. For rounding off, subtract the last 7 digits and multiply the previous one by one. The result is 4.65. Absolute rounding error in the first case
|4,647–4,64|= 0,007
in the second case
|4,647–4,65|= 0,003
is equal to the second convergence error is less than the first case. Therefore, it is preferable to round up with more than one example. To minimize the absolute approximation error, the following rule is used to round up positive numbers. If the first drop-down number is less than 5, then round it by at least, if this number is greater than or equal to 5, then round it up to the next. For example, rounding up to a tenth is 3,647 ≈ 3.6, 2.658 ≈ 2.7 we get in rounding to one hundred 0.6532 ≈ 0.65, 9,0374 ≈ 9.04 are formed. As can be seen from the foregoing, rounding numbers simplifies calculations.
3) An absolute error is used to compare the accuracy of different approximations of the same amount. If the convergence of different quantities is compared, an absolute error is not sufficient. For example, the distance from Tashkent to Fergana is 400 ± 1 km. The length of the pen is 21.3 ± 0.1 cm. In the first case, the absolute error is no more than 1 km and in the second case no more than 1 mm. Is it true that the length of the pen was more accurate than the distance from Tashkent to Samarkand? Absolute error in measuring the distance from Tashkent to Fergana not exceeding 1 km per 400 km. This means that the error is 1/400 ∙ 100 % ≈0.25 % of the measured size. Absolute error in measuring the length of the pen is not more than 0.1 cm by 21.3 cm. Therefore, the error in this case is 0.1/21.3 ∙ 100 % ≈ 0.47 % of the measured value.
Thus, the distance between cities was more precise than the length of the pen. To assess the quality of convergence, the concept of relative error is introduced. Relative error is the sum of the absolute error of a quantity with its approximate value module. Thus, if a number x is an approximate value, then an absolute error is | x-a | and the relative error is (| x-a |) / (| a |) . Relative error is usually expressed in percentages (percentages). After passing these topics, students will learn about absolute errors, rounding numbers, and relative errors. Pupils are exposed to these concepts in the 7th grade physics classroom. For example, in a class of physics in the 7th grade, “Flat-acceleration is moving determination of body acceleration” (Laboratory work 1).
The purpose of the work : The ball rolled down the sloping branch to determine the acceleration of a moving body with a straight acceleration by measuring the path and movement time.
Required equipment: metal rod, steel ball, rod, metal cylinder, measuring tape, stopwatch.

Fig. 1. Devices for the determination of the acceleration of smooth acceleration
The procedure of work includes the following steps:
- Install the metal rod on the shaft, as shown in Figure-1 the cylinder at the lower end.
- At the bottom of the ball, released from the upper end of the Nov measure the time elapsed before using the stopwatch.
- Repeat the experiment 3 times. Measure t 1 , t 2 , t 3 each time the ball is in motion. Record the results in Table 1.
- Measure the area S through the measuring tape.
- The path through which the body travels in a smooth accelerated motion S=at 2 / 2 the formula for acceleration from the formula is a = 2S/t 2 . S measured in the experiment Calculate the velocity a 1 , a 2 , a 3 , by placing the path and each time t 1 , t 2 , t 3 in the formula for acceleration.
- Calculate the average acceleration using the formula four a av = (a 1 + a 2 + a 3 )/3 . This value represents the acceleration of the ball rolling down the slope.
- Perform this experiment for three different slopes of the rod.
- ∆a n = | a av — a n | Find the absolute error in the formula.
- Calculate the average acceleration from the formula ∆a av = = (∆a 1 + ∆a 2 + ∆a 3 )/3 .
- Find the relative error in the formulas ε = (∆a n a av ) ∙ 100 % .
- Analyze the results and draw conclusions.
Table 1
|
т/р |
s, m |
t 1 , s |
t 2 , s |
t 1 ,s |
a 1 , m/s 2 |
a 2 , m/s 2 |
a 3 , m/s 2 |
a, m/s 2 |
a ўрт , m/s 2 |
|
|
1 |
||||||||||
|
2 |
||||||||||
|
3 |
This means that students will need to know the physical size measurements, what is the absolute error, the relative error, and the formula for finding this lab.
In conclusion, we need to pay attention to the sequence of topics in these textbooks to ensure continuity of topics in physics textbooks and the continuity of physics and mathematics. As we all know, a student who is well versed in mathematics is well versed in physics.
References:
- P. Khabibullaev, A. Boydedaev, A. D. Bakhromov, S. O. Burkhanov. «Physics textbook for 7th grade of secondary schools”.
- Sh. A.Alimov, O. R. Kholmuhamedov, M. A. Mirzaahmedov. «Algebra Textbook for Grade 7 of General Secondary Schools”.
- Sh. A.Alimov, O. R. Kholmuhamedov, M. A. Mirzaahmedov. «Algebra textbook for 8th grade of secondary schools”.
- Berulava M. N. Ying tegratsiya education content; — M.: Pedagogy, 1993 -- 170 p.
- Vetrova, V. T. Collection of physical problems for the general course of higher mathematics: Textbook. manual for universities. — Minsk: High school, 1997 -- 202 p.
- Demidovich B. P. Collection of problems and exercises in mathematical analysis: Textbook. manual for universities. — M.: AST, 2008 -- 558 p.
- Kiryushin I. V. Building interdisciplinary connections between mathematics and physics in the course of mathematical analysis using computer modeling of physical processes. Weight minute BDPU. I 3. — 2009. — № 4. — S.16–21.
- Kudryavtsev L. D. Modern mathematics and its teaching: Textbook. — M.: Nauka, 1985.-- 176 p.