Эта статья повещена разработке системы управления колесным мобильным роботом, предназначенным для обслуживания больниц. Рассмотрены аппаратные средства и программное обеспечение, необходимые для движения по сложной траектории и точного позиционирования. Автором предложен логический алгоритм управления движением, основанный на использовании запросов прерываний от датчиков. Он использовал гироскоп и энкодеры для измерения угловой и линейной скоростей робота и ПИД — регуляторы для управления приводами робота. Приведены результаты экспериментальных исследований макетного образца робота и определены ошибки его линейного и углового позиционирования. Исследовано движение робота по сложным реальным траекториям.
Ключевые слова: медицинский мобильный робот, система управления, ошибка позиционирования, экспериментальные исследования.
This article considers the control system of wheeled mobile robot, which is used as serve robot in hospital. The author designed the hardware and software of the robot for the moving along complex path accurately. Author proposed a logical control algorithm, which used interrupt requests from different robot sensors. He used gyroscope and encoders for the measuring angular and linear velocities of the robot and PID controllers in the drivers. Finally, the author made some real tests with different paths in hospital and analyzed errors.
Keywords: medical mobile robot, control system, positioning error, experimental tests.
Медицинские роботы относятся к роботам, используемым в больницах или клиниках для выполнения вспомогательных операций. Например, дезинфекция помещений, доставка пациентам лекарств, продуктов питания и предметов первой необходимости, транспортировка анализов, медицинской техники и оборудования, уборка мусора и т. д. Этот робот должен самостоятельно найти решение поставленной задачи, определить программу действий в соответствии с реальной ситуацией, а затем изменить последовательность действий, если это необходимо. По этим признакам его можно отнести к интеллектуальным сервисным роботам [1, 2].
В данной статье рассматривается система управления медицинским роботом и исследуются способы его движения по заданной траектории [3, 4]
Система управления
Общая структура предлагаемой системы управления показана на рисунке 1.
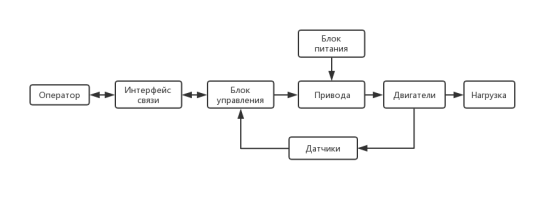
Рис. 1. Блок-схема системы управления
Задача, поставленная человеком — оператором через интерфейс связи поступает в блок управления, который находит вариант решения и формирует соответствующие сигналы управления для исполнительных устройств робота. Он также обеспечивает опрос датчиков во время движения для определения текущего положения и контроля окружающей среды. Если блок управления не может найти решения задачи, он обращается к оператору.
Использую информацию MEMS гироскопа, датчика угловых скоростей IMU и энкодеров микроконтроллер в реальном времени формирует сигналы управления силовыми приводами для движения по выбранной траектории. Одновременно микроконтроллер опрашивает ультразвуковые датчики и датчики столкновения чтобы исключить наезд на препятствия.
Блок-схема алгоритма основной программы управления [5, 6, 7] приведена на рисунке 2.
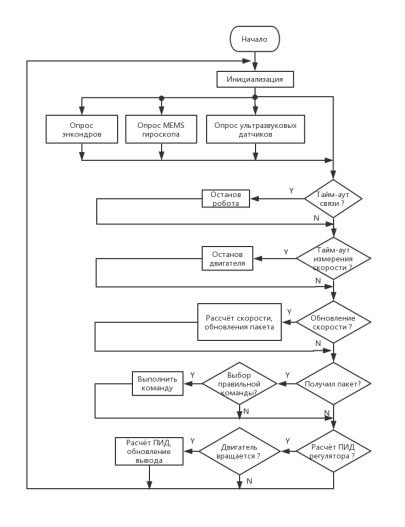
Рис. 2. Блок-схема алгоритма основной программы
Программа начинает работу с инициализации оборудования и данных, а затем переходит в состояние циклического сканирования флагов прерывания. При появлении запроса она отрабатывает подпрограмму прерывания и снова продолжает сканирование [8]. Основными источниками прерывания являются: порт USART, преобразователь «Код- ШИМ» и таймер.
Моделирование движения робота
Как отмечалось выше для медицинского мобильного робота была использована трехколесная кинематическая схема с двумя ведущими колёсами и одним пассивным [6]. Была изготовлен макетный образец для проведения экспериментов (рисунок 3). Некоторые характеристики модели приведены в таблице 1.
Таблица 1
Основные характеристики модели робота
|
Диаметр ведущих колес |
143 мм |
|
Размер работа |
400*290*260 мм |
|
Двигатель |
Мотор-редуктор постоянного тока |
|
Энкондер |
Фотоэлектрический инкрементный |

Рис. 3. Макет мобильного робота
Исследование линейного движения
Движение робота в плоскости xy показано на рисунке 4. Здесь красным цветом показана идеальная траектория движения робота, розовым цветом обозначено движение без ПИД регуляторов приводов, когда сигнал управления непосредственно подавался на преобразователь «КОД — ШИМ», а синим цветом показано фактическое положения робота при движении с использованием ПИД регуляторов [8, 9, 10] Зелёная прямая — результат аппроксимации реальной траектории с помощью уравнения
![]()
коэффициенты которого были получены по методу наименьших квадратов.
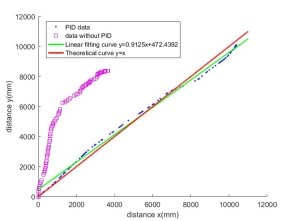
Рис. 4. Движение робота в плоскости xy
Имея два уравнения: первое — ![]() , для описания идеальной траектории, и второе —
, для описания идеальной траектории, и второе — ![]() для аппроксимации реальной траектории, была определена точность движения робота [11]. Ниже приведены средняя и среднеквадратичная ошибки, полученные по 88 измерениям (n=88)
для аппроксимации реальной траектории, была определена точность движения робота [11]. Ниже приведены средняя и среднеквадратичная ошибки, полученные по 88 измерениям (n=88)
![]() мм
мм
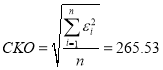 мм
мм
Исследование вращательного движения
Фактический угол поворота робота измеряется микропроцессором STM32 на основе данных акселерометра IMU. Основное уравнение инерциальной навигационной системы описывает изменение вектора скорости ![]() относительно земли, наблюдаемое в локальной системе координат, в данном случае, в системе координат робота
относительно земли, наблюдаемое в локальной системе координат, в данном случае, в системе координат робота
![]()
где![]() - измеренное значение акселерометра,
- измеренное значение акселерометра, ![]() - гравитационное ускорение,
- гравитационное ускорение,
![]() - угловая скорость вращения.
- угловая скорость вращения.
Поскольку инерциальная навигационная система измеряет значение ускорения, то скорость рассчитывалась методом направленного косинуса.
Уравнения изменения скорости углов выглядит следующим образом
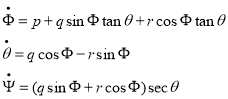
где![]() ,
,![]() ,
,![]() — углы тангажа, крена и рыскания, соответственно;
— углы тангажа, крена и рыскания, соответственно; ![]() – компоненты вектора скорости.
– компоненты вектора скорости.
Положение системы инерциальной навигации рассчитывается путём, интегрирования компонентов скорости. Результаты измерений угла поворота робота приведены в таблице 2.
Таблица 2
Результаты измерений угла поворота робота
|
Реальный угол |
Номер измерения |
Среднее значение | ||||
|
1 |
2 |
3 |
4 |
5 | ||
|
0° |
0 |
0 |
0 |
0 |
0 |
0 |
|
90° |
89.588 |
91.2469 |
91.6919 |
91.9995 |
90.412 |
90.98766 |
|
180° |
180.8459 |
181.7413 |
182.4445 |
179.2969 |
177.984 |
180.4625 |
|
270° |
268.1708 |
269.4452 |
270.3845 |
270.412 |
268.9563 |
269.7995 |
|
360° |
359.237 |
358.9893 |
359.9451 |
359.8022 |
360.022 |
359.599 |
На рисунке 5 показано угловое положение робота при повороте от 0 до 360 градусов. Как видно из рисунка, когда робот совершает вращательное движение стабильно и плавно без резких колебаний.
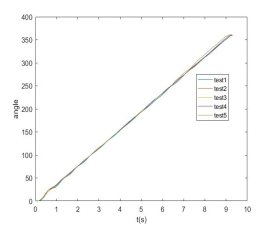
Рис. 5. Фактическое движение робота при вращении
По полученным результатам была вычислена средняя ошибка измерения угла поворота ![]() , значение которой не превысило 1 градус.
, значение которой не превысило 1 градус.
Экспериментальные исследования движения по траектории
Для подтверждения полученных результатов было проведено два эксперимента с реальным мобильным роботом [12]. В первом — робот несколько раз двигался по замкнутому маршруту, показанному на рисунке 6, и в начале координат (точке А) измерялась ошибка его позиционирования.
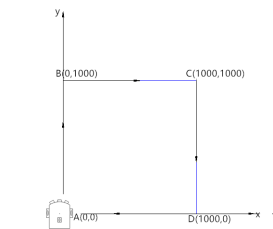
Рис. 6. Замкнутая траектория движения (размеры в мм)
Полученные значения ошибок по каждой координате приведены на графиках, показанных на рисунке 7. Рассеивание ошибки на плоскости xy показано на рисунке 8.
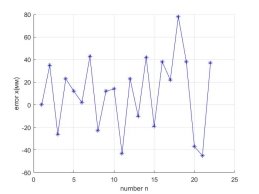
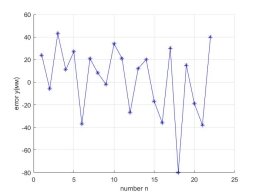
Рис. 7. Ошибки позиционирования робота в точке А
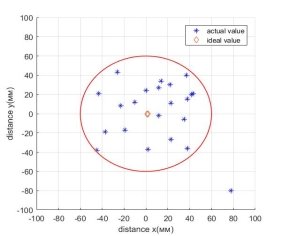
Рис. 8. График рассеяния ошибки в точке А
Из полученных данных видно, что при движении робота по траектории, представляющей квадрат 1000*1000 мм, ошибка находится в пределах окружности радиусом R=60 мм. Таким образом, ошибка позиционирования не превышает 1,5 % от общей длины достаточно сложной траектории, имеющей четыре поворота на 90 градусов.
Во втором эксперименте было исследовано движение робота по траектории, типичной для перемещения в помещении больницы, например во время доставки лекарств пациентам. Её вид показан на рисунке 15. Траектория имеет вид ломаной линии, отрезки которой равны: d1=1700 мм, d2=1600 мм, d3=700 мм, d4=1600 мм, d5=2400 мм, d6=1000 мм, d7=1000 мм, d8=200 мм.
![]()
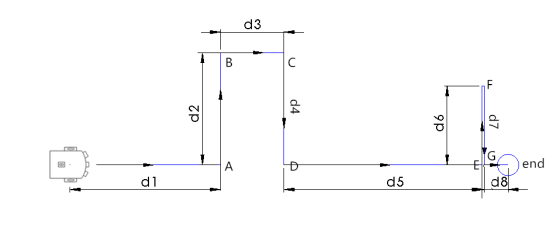
Рис. 9. Пример траектории движения робота в помещении больницы
Результаты экспериментов приведены в таблице 3, где ошибки позиционирования робота в точках A…G траектории обозначены буквами ε1…ε7, соответственно.
Таблица 3
Ошибки позиционирования вточках траектории (мм)
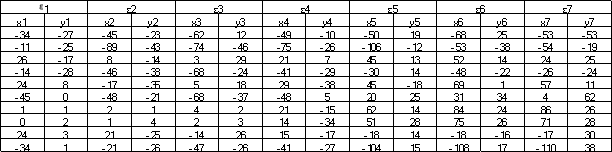
Графики изменения ошибок позиционирования в процессе движения от точки A до точки G (от 1 до 7) приведены на рисунке 10.
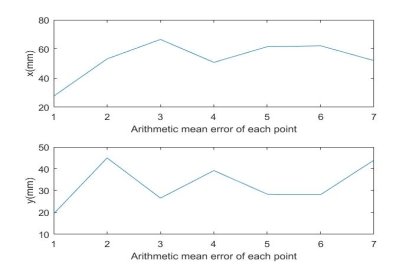
Рис. 10. Изменение ошибок позиционирования в процессе движения
В результаты проведенных экспериментов были определены средние и максимальные значения ошибок по отдельным координатам, а также предельная ошибка позиционирования на плоскости xy.
![]() мм
мм ![]() мм
мм
![]()
![]()
![]()
В последнем уравнении буквой ![]() (
(![]() = 1…7) обозначены точки от A до G, а буквой n — номер эксперимента. Таким образом, максимальная ошибка была получена в точке С во время десятого прохождения траектории роботом.
= 1…7) обозначены точки от A до G, а буквой n — номер эксперимента. Таким образом, максимальная ошибка была получена в точке С во время десятого прохождения траектории роботом.
Из полученных данных видно, что при движении робота по реальной траектории длиной 10,2 м, ошибка находится в пределах окружности радиусом R=320 мм. Таким образом, ошибка позиционирования не превышает 3,1 % от общей длины сложной траектории, имеющей шесть поворотов на 90 градусов и один разворот. Анализ показал, что ошибки, в основном, являются следствием не качественного крепления колес на макете роботе, которые имеют большой люфт в осевом и поперечном направлениях. Вторая причина ошибки — проскальзывание колёс по полу лаборатории, в которой проводились испытания.
Заключение
Разработанная система управления обеспечивает программное движение мобильного робота по сложным траекториям. Ошибка позиционирования в конечной точке составляет от 1 % до 3,1 %, в зависимости вида траектории. Экспериментальные исследования системы управления на макете мобильного показали, что она может быть использована для управления медицинскими работами. Эти результаты достигнут благодаря объединению данных с нескольких датчиков и использованию ПИД регуляторов в приводах робота.
Литература:
- Ющенко А. С., Тачков А. А. Управление пожарной робототехнической системой с использованием принципов диалогового управления: труды XXI Международной научно-технической конференции «Экстремальная робототехника» (Москва, 18–20 мая 2010 г.). — М., 2010. — С. 305–312.
- Мартыненко Ю. Г. Управление движением мобильных колесных роботов: Фундаментальная и прикладная математика. 2005. № 8. С. 29–80. //URL: http://www.mathnet.ru/php/archive.phtml?wshow=paper&jrnid=fpm&paperid=918&option_lang=rus
- Михайлов Б. Б., Девятериков Е. А. Система управления движением мобильного робота с визуальным одометром: Научно-технические ведомости Санкт-Петербургского государственного политехнического университета. Информатика. Телекоммуникации. Управление. 2013.- № 5 (181), с. 103–108.
- МАТЛАБ // URL: https://ww2.mathworks.cn/discovery/pid-control.html
- Muir P F, Neuman G P. Kinematic modeling of wheeled mobile robots [J]. Journal of Robotics Systems,1987,4(2):281–333. //URL: https://onlinelibrary.wiley.com/doi/abs/10.1002/rob.4620040209
- Fierro R,Lewis F L Control of a nonholonomic mobile robot:backstepping kinematics into dynamics [A]IEEE proceedings of 34th conference on decision and control [C],New Orleans,LA,December,1995:3805–3810.//URL:https://onlinelibrary.wiley.com/doi/abs/10.1002/(SICI)1097–4563(199703)14:3 %3C149::AID-ROB1 %3E3.0.CO;2-R
- Hagras H A. A Hierarchical Type-2 Fuzzy Logic Control Architecture for Autonomous Mobile Robots. IEEE Transactions on Fuzzy Systems, 2004, 12(4): 524–539.
- Thrun S, Burgard W, Fox D. A probabilistic technique for simultaneous localization and door state estimation with mobile robots in dynamic environments. In Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, 2002, 1: 521–526. //URL: http://dbpub.cnki.net/grid2008/dbpub/Detail.aspx?FileName=SSJD00000645937&DBName=SSJD&DBCode=SSJD&v=MTg0NjdtMm1jM2ZMWDdSN3FlYnVacEZpamtWNzNOSlZ3PU5qN0Jhck80SHRITXFZdEFiZWdJWTNzd3ptSVc3RXA5T1Fy
- K. Pathak, J. French, and S. K. Agrawal, “Velocity and position control of a wheeled inverted pendulum by partial feedback linearization,” IEEE Trans. Robot, 2005 21(3):505–513. //URL: https://ieeexplore.ieee.org/document/1435497
- Yue M, Hu P, Sun W. Path following of a class of non-holonomic mobile robot with underactuated vehicle body. IET Control Theory & Applications, 2010,4(10):1898–1904. //URL: http://d.scholar.cnki.net/detail/SJEV_U/SJEV13042000152822
- Arkin R C. Motor schema—based mobile robot navigation. The International journal of robotics research, 1989, 8(4): 92–112.
- Jiang Z P, Lefeber E, Nijmeijer H. Saturated stabilization and tracking of a nonholonomic mobile robot. Systems & Control Letters, 2001, 42(5): 327–332. //URL:http://kns.cnki.net/kcms/detail/detail.aspx?FileName=SJES13012300458967&DBName=SJES&DBCode=SJES&v=MDAwNDE4ZVdRTDN3WmVadUh5bmlVci9KSkZzVWF4cz1OaWZPZmJLN0h0RE9ySTlGWU80SEJYbytvQkVhNjB0NFRncmkzV2N4RA==

