Цель исследования данной статьи — определить основные причины, вследствие которых школьники совершают ошибки при решении неравенств; разобрать способы и методы решения некоторых видов неравенств; определить пути исправления возникающих ошибок, а в лучшем случае — вообще не допустить их появления. Рассматриваемая проблема актуальна и по сей день, более того, набирает обороты. И корни ее лежат не вовсе в специфичности конкретно неравенств или любых других видов математических задач. Значит, и пути решения проблемы также стоит искать в несколько более общих областях, о чем мы также поговорим в данной статье.
Ключевые слова: неравенства, свойства неравенств, правила неравенств.
The purpose of this article is to determine the main reasons why students make mistakes when solving inequalities; to analyze the ways and methods of solving some types of inequalities; to determine ways to correct errors that occur, and in the best case — to prevent them from appearing at all. The problem under consideration is still relevant to this day, moreover, it is gaining momentum. And its roots do not lie in the specificity of specific inequalities or any other types of mathematical problems. This means that you should also look for ways to solve the problem in a few more General areas, which we will also discuss in this article.
Keywords: inequalities, properties of inequalities, rules of inequalities.
Неравенства
Математика — наука об отношениях между объектами, о которых не известно ничего, кроме описывающих их некоторых свойств, — собственно эти свойства, качестве аксиом, положены в основание той или иной математической теории. История математики ведется издревле — от простейших операций подсчёта, измерения объектов и описания их формы. Создаются математические объекты с помощью идеализации свойств объектов реальных или других математических и записи этих свойств на формальном языке. К естественным наукам математика не относится, но широко в них используется — как для точной формулировки их содержания, так и для получения новых результатов. Математика — наука фундаментальная, поскольку она предоставляет другим наукам универсальные языковые средства; с помощью этого выявляется взаимосвязь наук, а также находятся общие законы природы.
Что же касается конкретно неравенств, то с ними начинают работать еще с детского сада. Детей учат тому, что в количественном соотношении некоторые объекты больше, а некоторые — меньше других. А есть объекты, которые равны между собой. В начальных классах продолжается изучение неравенств, там сравнивают — в какой чашке больше вишен, какое число больше, а какое меньше, далее следуют более сложные примеры, например — «4+2» больше, меньше или равно «3+3»?
Конечно, чем старше класс, тем сложнее, разнообразнее и интереснее становятся неравенства и пути нахождения их решений. Однако, стоит понимать, что сама суть неравенств и умение ее понимать находятся с человеком на протяжении всей его жизни. Да, мы об этом не задумываемся, но, тем не менее, постоянно решаем эти самые неравенства в своих бытовых делах. В этой пачке больше салфеток, но она стоит дороже, а в этой — меньше, но и стоит она дешевле. Что же выгоднее приобрести? Причем, ведь роль еще играют факторы того, сколько именно нужно сейчас салфеток и пригодятся ли потом лишние… В общем, рассуждать можно долго, этот пример приведен для того, чтобы было понятно — неравенства с нами всю жизнь и, даже если мы не используем математических формул для их решения (по крайней мере, осознанно), тема эта очень важная и актуальная. Тем более острой становится необходимость ее всестороннего изучения в школьной программе. И, как следствие — выявление проблем, трудностей и пробелов, возникающих у учеников. Именно эту проблему и хотелось бы затронуть в данной статье — какие ошибки допускают ученики при решении различных неравенств и какими способами эти ошибки можно исправить или даже избежать их вовсе.
Но прежде чем перейти к проблеме и способам ее решения, стоит немного поговорить о том, что же такое неравенство, каких видов они бывают и какие существуют пути решения.
Итак, что же такое неравенство?
Неравенство в математике — отношение, связывающее два числа или иных математических объекта с помощью одного из перечисленных ниже знаков.
Строгие неравенства
● — означает, что меньше , чем
● — означает, что больше , чем
Неравенства равносильны. Говорят, что знаки противоположны ; например, выражение «знак неравенства сменился на противоположный» означает, что заменено на или наоборот.
Нестрогие неравенства
–
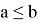
–
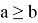
Про знаки ⩽ и ⩾ также говорят, что они противоположны .
Другие типы неравенств
–
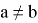
–

–
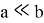
Связанные определения
Неравенства с одинаковыми знаками называются одноимёнными (иногда используется термин «одного смысла» или «одинакового смысла»). Допускается двойное или даже многократное неравенство, объединяющее несколько неравенств в одно. Пример:— это краткая запись пары неравенств: и
Числовые неравенства
Числовые неравенства содержат вещественные числа (для комплексных чисел сравнение на больше-меньше не определено) и могут содержать также символы неизвестных Числовые неравенства, содержащие неизвестные величины, подразделяются (аналогично уравнениям) на алгебраические и трансцендентные. Алгебраические неравенства, в свою очередь, подразделяются на неравенства первой степени, второй степени и так далее. Например, неравенство — алгебраическое первой степени, неравенство
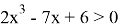
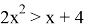
Существуют определенные правила решения неравенства
При решении неравенств используют следующие правила:
- Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, при этом знак неравенства не меняется.
- Обе части неравенства можно умножить или разделить на одно и то же положительное число, не изменив при этом знак неравенства.
- Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный.
Давайте рассмотрим несколько примеров.
1)
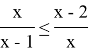
Переносим все в одну часть
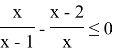
Приводим к общему знаменателю
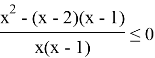
Раскрываем скобки, приводим подобные
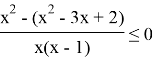
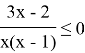
Находим точки, в которых числитель или знаменатель равны нулю.
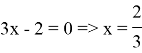
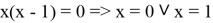
Отмечаем х на числовой прямой. Определяем знаки на каждом получившемся промежутке.
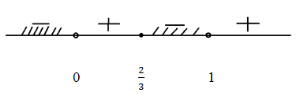
Записываем ответ
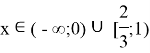
2)
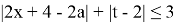
Заменим
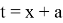
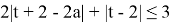
Раскрывая второй из модулей, запишем неравенство в виде системы
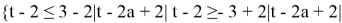
или
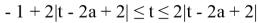
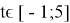
Ответ:
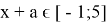
3)
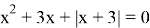
Раскрываем модуль по определению
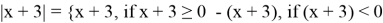
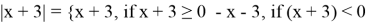
I случай
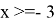
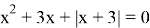
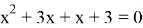
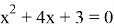
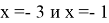
II случай

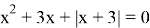
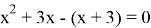
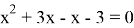
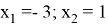
Ответ: x=-3; x=-1.
Неравенства включены в ЕГЭ повышенной сложности. Неравенства рассматриваются в 15 пункте под C3. Эти задания рассматриваются в 2 части экзамена, задания с 13–19 с развернутым ответом (полная запись решения с обоснованием выполненных действий), проверяющих освоение математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.
Задания части 2 работы предназначены для проверки знаний на том уровне требований, который традиционно предъявляется ВУЗами с профильным экзаменом по математике. Поэтому для более успешной сдачи экзамена, необходимо решить вторую часть, в которую входит тема неравенства.
И вот сейчас, определив и поняв — зачем же нужно уметь решать неравенства, мы переходим к обсуждению обозначенной выше проблемы.
Ошибки, допускаемые обучающимися при решении уравнений и неравенств.
Ошибки в этой сфере встречается самые разнообразные: от неверного оформления решения до ошибок логического характера.
- Одна из самых типичных ошибок состоит в том, что учащиеся при решении уравнений и неравенств без дополнительных пояснений используют преобразования, нарушающие равносильность, что приводит к потере корней и появлению посторонних корней.
- Целая группа ошибок, а точнее будет сказать — недочетов, состоит в том, что учащиеся не уделяют должного внимания нахождению области определения уравнений, хотя именно она в ряде случаев есть ключ к решению.
- Типичной ошибкой учащихся является то, что они не владеют на нужном уровне определениями понятий, формулами, формулировками теорем, алгоритмами.
- Многие ошибки, допускаемые при решении уравнений и неравенств, являются следствием того, что учащиеся очень часто пытаются решать задачи по шаблону, привычным путем, даже не задумываясь о том, что стоит посмотреть на задачу с другой стороны.
- Ряд типичных ошибок связан с тем, что учащиеся не совсем корректно решают уравнения и неравенства на основе функционального подхода.
- При решении неравенств с помощью подстановки мы всегда сначала решаем новое неравенство относительно новой переменной, и лишь в его решении делаем переход к старой переменной. Школьники же очень часто ошибочно делают обратный переход раньше. Этого делать не следует.
- Типичная ошибка при решении уравнений, неравенств и их систем состоит в том, что неверно преобразовываются выражения.
Способы исправления и предупреждения ошибок
Как и в случае с любой проблемой, после ее обозначения и осознания, должны искаться пути решения. Иначе говорить о проблеме становится бессмысленно. Как мы видим, многие ошибки возникают у учащихся в следствие спешки или же невнимательности. А зачастую одно приводит к другому. Поэтому для исправления и предупреждения многих ошибок важно сформировать у школьников навыки самоконтроля . Эти навыки состоят из двух частей:
а) умения обнаружить ошибку;
б) умения её объяснить и исправить.
В процессе обучения применяются несколько приёмов самоконтроля, которые помогают обнаружить допущенные ошибки и своевременно их исправить. К ним относятся:
– проверка вычисления и тождественного преобразования путём выполнения обратного действия или преобразования;
– проверка правильности решения задач путём составления и решения задач, обратных к данной;
– оценка результата решения задачи с точки зрения здравого смысла;
– проверка аналитического решения графическим способом.
Сведению вероятности ошибок к минимуму также способствуют следующие профилактические меры:
– Тексты письменных заданий должны быть удобными для восприятия: грамотно сформулированными, хорошо читаемыми.
– Активная устная отработка основных ЗУН, регулярный разбор типичных ошибок.
– При объяснении нового материала предугадать ошибку и подобрать систему заданий на отработку правильного усвоения понятия. Акцентирование внимания на каждом элементе формулы и выполнение разнотипных заданий позволит свести ошибочность к минимуму.
– Подбирать задания, вызывающие интерес, формирующие устойчивое внимание.
– Прочному усвоению (а, значит, отсутствию ошибок) способствуют правила, удобные для запоминания, четкие алгоритмы, следуя которым заведомо придешь к намеченной цели.
Каждый учитель знает, что планомерное и систематическое повторение и есть основной помощник в ликвидации пробелов, а, следовательно, и ошибок. В математике, как ни в какой другой науке, особенно сильна взаимосвязь материала. Изучение и понимание последующего невозможно без знания предыдущего, отсюда возникает неизбежность повторения на каждом уроке. При объяснении нового материала следует использовать ряд определений и теорем, которые были изучены ранее. Тем самым новые знания будут основываться на уже сформировавшейся и закрепившейся базе, что приведет к лучшему усвоению материала. Поэтому так важен, особенно в математике, комплексный и систематический подход к обучению. С самых первых дней обучения важно заложить первые кирпичики той базы, на которую в дальнейшем будут надстраиваться новые знания. Несомненно, главную роль здесь играют способности самого ученика, но проявить и дать направление их развитию — тут уже как раз поле деятельности, которое зависит от таланта и способностей учителя, а также от влияния семьи и окружения. Не только в рассматриваемой сегодня теме, но и в процессе обучения в целом. Ведь, как мы видим, ошибки в решении неравенств возникают именно вследствие пробелов в образовательном процессе в целом, а не из-за специфичности конкретно данного раздела. Так и пути решения и исправления описанных ошибок вовсе не специфичны и уникальны, они сводятся к тому, что сначала надо устранить и/или предупредить общие пробелы в знаниях, не натаскать ребенка на конкретные шаблоны, а именно научить разбираться в рассматриваемом вопросе.
Литература:
- Математика [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeR~s
- Неравенство [Электронный ресурс] / Википедия — Режим доступа: https://goo-gl.ru/6qeV~s
- Анализ типичных ошибок при решении неравенств [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeW~s
- Решение неравенств: основные ошибки и полезные лайфхаки [Электронный ресурс] / — Режим доступа: https://goo-gl.ru/6qeY~s
- Методическое пособие. Неравенства и системы неравенств [Электронный ресурс] / Инфоурок — Режим доступа: https://goo-gl.ru/6qeZ~s
- https://infourok.ru/user/ivanova-antonina-mihaylovna/blog/problemitipichnie-oshibkidopuskaemie-uchaschimisya-pri-reshenii-uravneniy-i-neravenstv-48897.html

