В данной работе представлен сравнительный анализ математической модели реактора со сосредоточенными параметрами с наиболее распространенных системами автоматического регулирования — пропорциональной и релейной. В SIMULINK MATLAB получены переходные процессы по возмущающему воздействию, а также оценены устойчивости разработанных САР при изменении параметров системы.
В настоящее время к системам внешнего регулирования мощности реактора выдвигаются следующие требования:
а) поддержание заданного уровня мощности с достаточно высокой точностью;
б) исключение ложных срабатываний системы аварийной защиты (АЗ) за счет колебательных процессов в органах регулирования;
в) система автоматического регулирования мощности должна работать как в режиме стабилизации заданного уровня мощности, так и в режиме слежения за изменяющейся мощностью.
Главное отличие между двумя типами данных систем заключается в том, что в пропорциональной АСР перемещение стержня пропорционально ошибке регулирования и направлено в сторону ее уменьшения, а в релейной системе наличие зоны нечувствительности реле приводит к возможности возникновения автоколебательного режима при неточной настройке регулятора. Поэтому, чтобы не усугублять ситуацию, требуется, чтобы реактор был устойчивым объектом управления, то есть обладал свойством самовыравнивания, что возможно только при отрицательном температурном коэффициенте реактивности реактора.
В качестве математической модели в текущей работе используется система уравнений, описывающих динамику неотравленного ксеноном и самарием реактора, работающего в энергетическом диапазоне мощности.
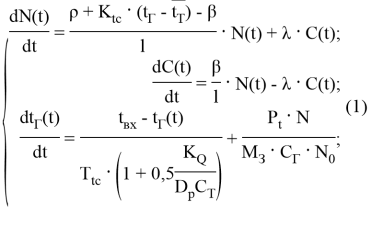
Уравнения, раскрывающие взаимосвязь между величинами:
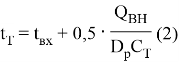
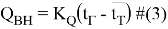
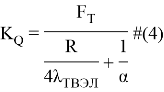
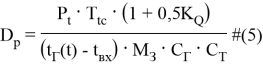
где
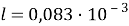
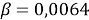
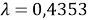
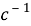
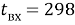
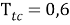
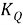
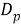
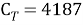
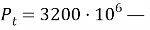
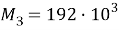
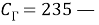
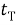
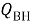
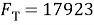
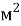
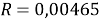
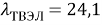
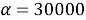
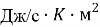
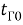
Эти уравнения не имеют смысла без следующих начальных условий:
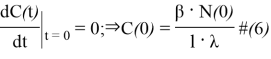
Данная модель имеет следующее ограничение: она составлена для реактора со сосредоточенными параметрами, тем самым предполагается, что за время процесса, который вносит избыточную реактивность пространственное распределение нейтронного поля реактора совершенно не изменяется. Для реализации данной математической модели реактора в SIMULINK используется блок MATLAB S-function.
Также для уточнения расчетов математическая модель регулирующего стержня представлена в виде нелинейной функциональной зависимости, описывающейся следующим уравнением:
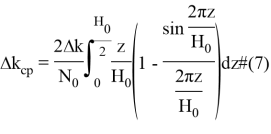
где
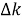
z — глубина погружения, см;
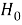
На основании вышеизложенного в SIMULINK MATLAB была составлена следующая схема, приведенная на рисунке 1:
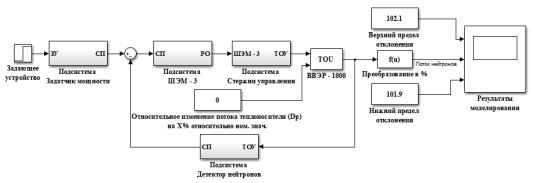
Рис. 1. Математическая модель САР ядерного реактора
Управление реактором осуществляется с по принципу обратной связи. Увеличение плотности потока тепловых нейтронов влечет за собой увеличение тока ионизационной камеры. Токи ионизационной камеры достаточно малы, поэтому их необходимо усилить. Ток на выходе из усилителя сравнивается по значению с токами ручного задатчика мощности. Затем сигнал рассогласования поступает на регулятор мощности, сигнал с которого усиливается тиристорным усилителем и поступает на шаговый электромагнитный привод, который осуществит перемещение регулирующего стержня и скомпенсирует скачок реактивности, что приведет к изменению нейтронной мощности реактора.
Переходные процессы для пропорциональной и релейной САР представлены на рисунках 2 и 3 соответственно.
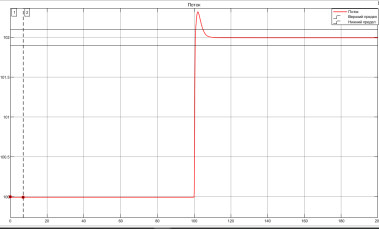
Рис. 2. Переходный процесс при наборе мощности со 100 % до 102 % от номинальной в пропорциональной АСР
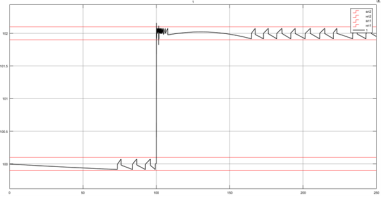
Рис. 3. Переходный процесс при наборе мощности со 100 % до 102 % от номинальной в релейной АСР
Можно сказать, что релейная САР обеспечивает лучшие показатели качества регулирования. Однако, автоколебательный процесс может привести к быстрому износу исполнительного механизма. Показатели качества регулирования двух систем сведены в таблицу 1.
Таблица 1
Показатели качества системы внешнего регулирования
|
Пропорциональная АСР |
Релейная АСР |
|
=5.8 % |
=0.5 % |
|
T рег = 2.1 с |
T рег = 1,92с |
Для сравнения устойчивости АСР к нестабильности параметров динамической модели, можно сымитировать несколько ситуаций: изменение коэффициента передачи шагового привода ввиду износа, изменение коэффициента передачи ионизационной камеры ввиду выгорания, ухудшение свойств поглощающего стержня. Смоделированные системы управления могут скомпенсировать данные воздействия, однако прямые показатели качества заметно ухудшаются. Переходные процессы для релейной АСР при изменении параметров системы представлены на рисунках 4 и 5 соответственно.
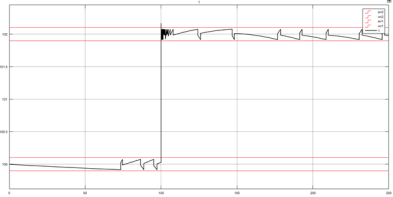
Рис. 4. Переходный процесс при изменении коэффициента передачи ШЭМ
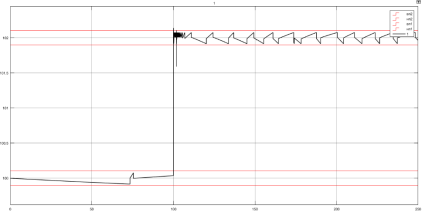
Рис. 5. Переходный процесс при изменении коэффициента передачи ИК
Для обеспечения качества регулирования при отличном от текущего возмущающим воздействиям в подсистему ШЭМ встроен PID-регулятор Simulink. С помощью встроенной в SIMULINK настройкой “PID — Tune” с автоматическим подбором коэффициентов регулятора можно добиться желаемых результатов при любых типах возмущающих воздействий.
Литература:
- Бартоломей Г. Г. Основы теории и методы расчета ядерных энергетических реакторов / Бартоломей Г. Г., Бать Г. А., Байков В. Д., Слухов М.С — М.: Энергоатомиздат, 1989–512с.;
- Галанин А. Д. Введение в теорию ядерных реакторов на тепловых нейтронах / Галанин А. Д. — М.: Энергоатомиздат, 1990–536с;
- Дементьев Б. А. Кинетика и регулирование ядерных реакторов / Дементьев Б.А — М.: Атомиздат, 1986. — 272с
- Фейнберг С. М. Теория ядерных реакторов / Фейнберг С.М, Шихов С. Б., Троянский В. Б. — М.: Атомиздат,1978. — 400с;
- Шульц М. А. Регулирование ядерных энергетических установок / Шульц М. А. — М.: Издательство иностранной литературы,1957–460с.







