В статье авторы, исходя из определения внутрипредметных связей, провели реализацию урока, учитывающего эти связи, в образовательном процессе (проведение урока по математике в 8 «Г» классе МБОУ «СОШ № 25 г. Абакана».
Ключевые слова: внутрипредметные связи, обучение, математика
В образовательном процессе наиболее часто применяется термин «Межпредметные связи», отражающие различные виды связей между предметами. Однако, упоминая о данном виде связей, в методической литературе забывают о внутренних связях между разделами конкретной науки. Речь пойдет о внутрипредметных связях.
Данные связи широко изучаются и раскрывают свою суть в пособии В. А. Далингера [2]. Автор раскрывает понятие «внутрипредметные связи» в более широком контексте, исследует их в обобщающем повторении.
Опираясь на исследование А. А. Аксенова [1], дадим определение внутрипредметным связям.
Определение: Внутрипредметными связями называют связи, соединяющие составные части определенной дисциплины или предмета.
А. А. Аксенов в своем исследовании [1] выделяет безусловные и условные внутрипредметные связи. Безусловными внутрипредметными связями между двумя субъектами называют те связи, истинность или ложность одного субъекта находится в зависимости от другого субъекта. Если же истинность или ложность одного субъекта не зависит от другого субъекта, то данные внутрипредметные связи называют условными.
Выделяют два вида внутрипредметных связей: логические и аналитические. Различие между ними состоит в том, что для логического вида внутрипредметных связей решение задачи требует определенные логические закономерности, в то время как для аналитического вида данные закономерности не требуются.
Основываясь на данных определениях, мы разработали конспект урока по алгебре для 8 класса на тему «Геометрические методы решения квадратных уравнений».
Урок алгебры в 8 классе.
Тема урока: Решение квадратных уравнений геометрическим способом.
Учебник: [3], [4], [5]
Цели урока:
Изучить геометрический метод решения квадратных уравнений, научиться решать задачи по данной теме.
Задачи:
- Познакомить с геометрическим способом решения квадратных уравнений, а также с составлением алгоритмов для данного способа решения квадратных уравнений.
- Развивать интеллектуальные возможности учащихся, различные формы мышления, познавательных интересов, творческих способностей учащихся.
- Воспитать интерес к математике, учиться работе с различными видами задач, содействовать восприятию учебного материала, научить работать в команде.
Тип урока: урок изучения нового материала.
План урока:
- Организационный момент (1 мин.).
- Актуализация знаний учащихся (5 мин.).
- Изучение нового материала (22 мин.).
- Первичное закрепление изученного материала (15 мин.).
- Домашнее задание (1 мин.).
- Итог урока (1 мин.).
Используемые приемы иметоды обучения: познавательный, систематизирующий, коммуникативный, логический
Средства обучения: учебник, учебные пособия, геометрические инструменты, средства мультимедиа.
Ход урока
I. Организационный момент.
Здравствуйте! Сегодня мы познакомимся с интересным методом решения квадратных уравнений — геометрическим методом. Мы с вами научимся составлять алгоритмы данного способа решения квадратных уравнений и порешаем задачи по данной теме.
II. Актуализация знаний учащихся.
Вставить пропущенные слова (буквы, знаки)
Вариант 1.
а) Если 
— квадратное уравнение, то 
называют … коэффициентом, 
… коэффициентом, 
— … членом.
б) Корни квадратного уравнения вычисляются следующим образом:
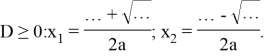
в) Квадратное уравнение вида 
называют …
г) Теорема Виета утверждает, что в уравнении вида 
…; 
.
Вариант 2.
а) Если — квадратное уравнение, то первый коэффициент — это число …, второй коэффициент — это число …, свободный член — это число ….
б) Корни квадратного уравнения вычисляются следующим образом:
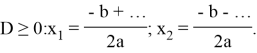
в) Приведенное квадратное уравнение — это уравнение вида ….
г) Теорема Виета утверждает, что в уравнении вида …; .
III. Изучение нового материала
Раньше, когда только начинали зарождаться различные цивилизации, математика начинала свое развитие с геометрии. Геометрические задачи имели здесь больший приоритет, чем алгебраические, и это было связано с тем, что необходимо было производить измерительные работы на местности. В частности, Евклид именно написал свои знаменитые «Начала» именно по этой самой причине. Квадратные уравнения имеют, помимо геометрического метода, различные способы решения. Но наш метод выбран именно потому, что здесь наглядно показывается, как происходит решение квадратных уравнений с точки зрения измерения различных площадей участков (здесь уже мы будем рассматривать геометрический смысл квадратных уравнений).
Пример. Решить уравнение 
(1)
Для ее решения рассматривается квадрат (рис. 1) с искомой стороной 
, на сторонах которого строятся прямоугольники так, что другая сторона каждого из них равна 
, следовательно, площадь каждого равна 
. Полученную фигуру дополняют затем до нового квадрата 
, достраивая в углах четыре равных квадрата, сторона каждого из которых равна , а площадь 
. Тогда площадь 
квадрата можно представить как сумму площадей: первоначального квадрата (
, четырех прямоугольников (
) и четырех пристроенных квадратов (
), т. е.
(2)
Заменяя в (2) 
числом 39, согласно (1), получим 
, откуда следует, что сторона квадрата , т. е. отрезок 
, равна 8. Для искомой же стороны первоначального квадрата получим:
Такое геометрическое построение соответствует следующим алгебраическим преобразованиям при решении уравнения 
1) 
2) 
3) 
4) 
Последнее и представляет правило ал-Хорезми для решения указанного квадратного уравнения [36].
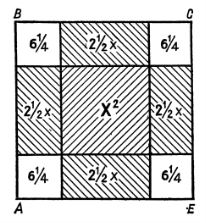
Рис. 1. Геометрическое решение квадратного уравнения
IV. Первичное закрепление изученного материала.
Решить геометрическим способом уравнения:
а) 
б) 
а) Решение представлено на рис. 2, где
или 
.
Выражения 
и 
геометрически представляют собой один и тот же квадрат, а исходное уравнение 
— одно и то же уравнение. Откуда и получаем, что 
, или 
, 
.
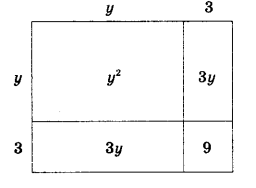
Рис. 2. Решение квадратного уравнения 
б) Преобразуя уравнение, получаем 
.
На рис. 3 находим «изображения» выражения 
, т. е. из площади квадрата со стороной 
два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению прибавить 9, то получим площадь квадрата со стороной 
. Заменяя выражение равным ему числом 16, получаем: 
, т. е. 
, или 
, где 
, 
.
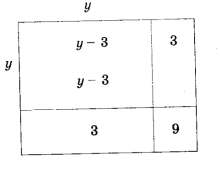
Рис. 3. Решение квадратного уравнения
V. Домашнее задание.
Решить геометрическим методом уравнения из номера 24.22 на с. 152 учебника [4].
VI. Итог урока.
Ребята, что вам запомнилось сегодня на уроке? Понравился ли вам урок? Чем понравился? (Дети отвечают на вопросы).
Теперь приведем комментарии к тому, как проходил данный урок в школе.
Урок по алгебре на тему «Геометрический способ решения квадратных уравнений» проходил в 8 «Г» классе в МБОУ «СОШ № 25 г. Абакана». Целями проведения урока были следующими:
− поскольку по теме «Квадратные уравнения» выделяется, на мой взгляд, недостаточное количество часов, мне пришлось выделить из резерва учебных часов отдельный урок, так как считаю, что эта тема достаточно интересна и увлекательна для детей;
− по данной теме не проводятся уроки, в школьных учебниках данный метод не описывается; кроме того, эта тема изучается либо в классах с углубленным изучением математики, либо на различных элективных и факультативных занятиях;
− уникальность данной темы заключается в том, что, в основном, методика обучения способам решения квадратных уравнений сводится к выделению дискриминанта и нахождению корней или при помощи теоремы Виета. Данный способ решения квадратных уравнений, грубо говоря, «разрушает стереотипы» преподавания и разработок учебных планов по математике.
Сложность проведения урока заключалась в том, что он проходил в не совсем обычном формате. В связи с неблагоприятной эпидемиологической обстановкой (распространение коронавирусной инфекции COVID-19), урок проходил в дистанционной форме с использованием платформы Skype, кроме того, использовались ресурсы образовательного портала uchi.ru.
Из-за того, что такой способ преподавания совершенно новый, уникальный, многие дети, или по незнанию, или по техническим причинам не смогли принять участие в уроке, им был выслан в электронном журнале «Барс. Web-образование» конспект урока, который представлен в данной работе. Непонятные для ребят вещи оперативно решались посредством телефонной связи, мессенджеров What’s App, Viber, а также через электронную почту.
Начинался процесс обучения с того, что дети заходили на платформу Skype, они включали на своих компьютерах или смартфонах камеру и микрофон, чтобы была обратная связь. Затем был включен графический редактор Paint, чтобы можно было записывать ход решения учебного примера (пример представлен в конспекте урока). Заранее были приготовлены необходимые УМК по алгебре, в том числе электронные ресурсы, была включена демонстрация экрана для отображения наглядности урока.
Урок начался с озвучивания темы урока, целей, задач темы. После им было предложено задание, смысл которого заключался в том, чтобы в предложения, в которых рассказывалось о квадратных уравнениях и способах их решений, нужно вставить подходящие по смыслу слова.
После этого упражнения начался этап изучения нового материала. В ходе данного этапа дети слушали внимательно, но, поскольку тема была новая и не совсем обычная, было много вопросов с их стороны; вопросы были по теме и, таким образом, не нарушали общей картины проведения урока. Рассказывая о данном методе, был сделан упор на исторические факты, на основе которых и был сформирован данный урок.
После начался этап закрепления изученного материала. Учащимся были предложены задания для первичного закрепления нового материала, а именно, решение уравнений геометрическим способом. В ходе данного этапа не все учащиеся смогли правильно решить задачу, поскольку интерпретация данного урока оказалась немного сложной и у них возникли определенные трудности. Но после того как было проведено разъяснение решения одной задачи, учащиеся смогли решить оставшееся задание.
Домашним заданием стал номер из учебника [4], условие которого поменялось в связи с вводом новой темы. В этот же день учащиеся прислали мне выполненную домашнюю работу через мессенждеры What’s App, Viber, в социальной сети «ВКонтакте», а также через электронную почту.
Теперь, основываясь на том, как проходил урок, можно составить методический анализ урока.
Схема анализа урока (по Г. И. Саранцеву [33]):
1. Общие сведения об уроке
Школа: МБОУ «СОШ № 25 г. Абакана»
Класс: 8 «Г»
Предмет: алгебра
Учитель: Петров Владислав Игоревич
Тема урока: Геометрический способ решения квадратных уравнений
Цель урока: Изучить геометрический метод решения квадратных уравнений, научиться решать задачи по данной теме.
Тип урока: урок изучения нового материала.
2. Организация урока
1. Готовность учителя к уроку.
Учитель подготовился к уроку должным образом: подготовил конспект урока, компьютер для выхода в Интернет и осуществления образовательной деятельности, проверил Интернет-соединение, подготовил учебники, методические пособия.
2. Готовность учащихся к уроку.
Учащиеся подготовились к уроку должным образом: подготовили компьютеры для выхода в Интернет с целью усвоения новых знаний, подготовили тетради, учебники, различные канцелярские принадлежности.
3. Подготовленность классного помещения.
В связи с неблагоприятной эпидемиологической обстановкой, вызванной пандемией коронавирусной инфекцией, урок проходил в дистанционном режиме с применением online-технологий в платформе Skype. Участники образовательного процесса подготовили камеры и микрофоны для обратной связи.
4. Мобилизирующее начало урока.
Мотивация урока прошла на отлично, дети были подготовлены полностью.
3. Структура урока
1. Этапы урока, распределение времени.
- Организационный момент (1 мин.).
- Актуализация знаний учащихся (5 мин.).
- Изучение нового материала (22 мин.).
- Первичное закрепление изученного материала (15 мин.).
- Домашнее задание (1 мин.).
- Итог урока (1 мин.).
2. Четкость этапов, выделение главного.
Здесь шесть главных этапов, они все взаимосвязаны, соответственно, главных этапов тоже шесть.
3. Соответствие структуры урока целям и содержанию его.
Структура урока соответствует целям урока, ведь по цели урока выделяют соответственно и этапы урока, так как все это зависит от типа урока.
4. Насыщенность урока и темы.
Данная тема достаточно интересна и уникальна, поскольку она встречается только в элективных и факультативных курсах по математике, она вызвала у меня интерес.
5. Сочетание коллективной, групповой и индивидуальной работы с учащимися.
В дистанционном обучении применяются, в основном, фронтальный и индивидуальный способы работы с учащимися. Я использовал оба метода, т. к. каждый учащийся должен понимать, что математика является важнейшей наукой.
4. Содержание урока
1. Объем фактического материала, соответствие программе и уровню знаний учащихся.
Данная тема является необязательной и рассчитана на 1 час, она не включена в календарно-тематическое планирование по алгебре, на реализацию данного урока был выделен резервный урок по математике. Тема рассчитана на учащихся, которые прошли тему «Квадратные уравнения» и познакомились с методами решения квадратных уравнений.
2. Научность изложения материала, единство образовательной и воспитательной функций.
Изложение материала проходило на научном языке с применением различной терминологии. Здесь проходило единство образовательной и воспитательной функции, поскольку здесь затрагивается история математики, и учащиеся должны понимать, что математика — древняя наука и с уважением относиться к ученым, которые работали усердно над ней.
3. Соответствие теории и упражнений.
Упражнения полностью соответствуют теории, поскольку в упражнениях присутствуют задания, аналогичные примеру в теоретическом материале.
4. Повторение пройденного, опорные знания.
Перед тем, как начать изучение новой темы, была проведена актуализация пройденных ранее знаний. Здесь учащимся было предложено следующее задание: вставить слова в предложения, в которых рассказывалось о квадратных уравнениях и методах их решения.
5. Внутрипредметные и межпредметные связи, связь с жизнью.
Так как тематика ВКР посвящена внутрипредметным связям, то здесь присутствует внутрипредметная связь логического типа с выделением глобальной и локальной логических структур задачи. Межпредметные связи включали связь математики и истории. Что касается связи с жизнью, то данный метод ранее применялся в измерении площадей различных земельных участков.
5. Методы, приемы исредства обучения
1. Целесообразность методов обучения
Выбранные методы обучения являются взаимодополняющими, поскольку они предполагают полноценное проведение урока по данной теме.
2. Достижение основных принципов дидактики в обучении.
Все основные принципы дидактики (научности, доступности, целенаправленности, систематичности и последовательности, наглядности, связи обучения с жизнью, сознательности и активности, прочности, воспитания и развития) при изучении новой темы были учтены и соблюдены в той или иной степени.
3. Познавательная активность учащихся и роль учителя на уроке.
Познавательная активность проявлялась в том, что они внимательно слушали учителя, спрашивали непонятные для них вещи, уточняли моменты, а одна ученица даже рассказала, что она знала про ученого ал-Хорезми. Учитель же, направлял и мотивировал их на получение знаний, был в роли научного консультанта, был рассказчиком новой темы.
4. Наличие обратной связи «учитель — ученик».
В ходе урока была осуществлена обратная связь «учитель — ученик». Она заключалась в том, что учитель задавал наводящие вопросы, а учащиеся на эти вопросы отвечали, и наоборот.
5. Развитие логического мышления у учащихся и самостоятельность в обучении.
Логическое мышление у учащихся развивалось посредством решения задач по теме урока, при решении задач происходила самостоятельная работа, когда они, ни с кем не советуясь, делали задание.
6. Работа со слабоуспевающими учащимися.
После урока слабоуспевающие учащиеся оставались на некоторое время в видеозвонке, чтобы еще раз пояснить основные моменты новой темы. Кроме того, много было учащихся, кто не смог подключиться по разным причинам. Среди них были и слабые ученики, им приходилось по телефонной связи объяснять новую тему.
7. Методы проверки и оценки знаний учащихся.
За этот урок отметки выставлялись по наличию правильно выполненного домашнего задания. Если все было верно и все задания были выполнены, ставилась оценка «5», если были 1–2 ошибки — «4», если 2–3 ошибки или не выполнено одно-два задания — «3», если дела обстояли хуже или совсем отсутствовала работа — «2».
8. Средства достижения и поддержания внимания учащихся на уроке и интереса к предмету.
При обучении использовались следующие средства достижения и поддержания внимания:
− усиление впечатления прямым путем — возвышая голос, подчеркивая слова;
− прямое требование внимания путем частого обращения к учащимся;
− занимательность преподавания.
9. Итог урока, его воспитательная ценность.
Итог урока прошел следующим образом: учащимся были заданы вопросы о том, понравился ли им урок.
6. Учитель как личность
1. Знания и методическая грамотность учителя.
Мои знания в качестве учителя по своему предмету находятся чуть выше среднего уровня, что касается методической грамотности, то ее необходимо оттачивать.
2. Культура речи и педагогический такт.
Речь у меня, как у учителя математики, соответствует уровню среднестатистического учителя, но в моей речи присутствуют много слов-паразитов, засоряющих речь. Что касается педагогического такта, то он находится на высшем уровне.
3. Доброта и требовательность к учащимся.
К учащимся относился с уважением, требовал от них того же, что я и получил. Требования были стандартные, чтобы они все выполняли и сдавали вовремя, также по возможности присутствовали на уроках.
4. Контакт учителя с учащимися.
С учащимися контакт проходил на уроке по содержанию темы.
7. Заключение по уроку
1. Эффективность урока.
Данный урок будет уместен в тех классах, где изучают на углубленном уровне алгебру. К сожалению, данная тема не находит отражения в базовых темах по алгебре.
2. Ценные стороны урока и недостатки.
Урок проходил в необычном формате, что само собой является плюсом, прорывом в образовании, но является и минусом, поскольку теряются все очные связи с учащимися. Что касается содержания урока, то тема достаточно сложная, но интересная, так что однозначно сказать насчет положительных и отрицательных сторон нельзя.
3. Предложения учителю.
По возможности сделать упор на изучение различных методик обучения математики, чтобы не проводить уроки однообразно.
Литература:
- Аксёнов А. А. Теоретические основы реализации внутрипредметных связей посредством решения задач в классах с углублённым изучением математики. — Орёл, 2000
- Далингер В. А. Методика реализации внутрипредметных связей при обучении математике. — М.: Просвещение, 1991
- А. Г. Мордкович. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений — М.: Мнемозина, 2013
- А. Г. Мордкович и др. Алгебра. 8 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений — М.: Мнемозина, 2013
- Глейзер Г. И. История математики в школе VII — VIII кл. Пособие для учителей. — М.: Просвещение, 1982
