Отображения, сохраняющие нулевые произведения

При изучении алгебр линейных операторов отображения между ними играют важную роль. Отображения, такие как изоморфизм, гомоморфизм, дифференцирование и автоморфизм различных алгебр операторов, определённых в гильбертовых пространствах, были изучены во многих работах([1]- [5]).

В 1997 г. Шемрлом [2], было введено понятие 2-локального автоморфизма и 2-локального дифференцирования, и в этой работе он рассматривал отображений на алгебре всех линейных ограниенных операторов на гильбертовом пространстве, в бесконечномерном сепарабельном случае, показав, что если — бесконечномерное сепарабельное гильбертово пространство, тогда каждый 2-локальный автоморфизм алгебры является автоморфизмом. Аналогичный результат был получен для 2-локального дифференцирования.

В 2004 г. [3] было получено аналогичное описание для конечномерного случая, а именно доказано, что если — алгебра матриц над комплексными числами, и 2-локальный *– автоморфизм на этой алгебре, тогда является *автоморфизмом.

В работе Аюпова и Кудайбергенова [4] были изучены 2-локальные дифференцирования и 2-локальные автоморфизмы на алгебре всех линейных ограниченных операторов на произвольном гильбертовом пространстве и было показано, что если — произвольное гильбертого пространство, — алгебра всех ограниченных линейных операторов на , тогда каждый 2-локальный автоморфизм на этой алгебре, является автоморфизмом.

Многие ученые изучали и аддитивные, или линейные отображения, сохраняющие нулевые произведения, в которых одно из отображений в операторных алгебрах, и в большинстве случаев показано, что отображение сохраняет нулевого произведение тогда и только тогда, когда отображение записано в виде умножения гомоморфизма с центральным элементом алгебры.

Пусть — гильбертово пространство, — алгебра всех линейных ограниченных операторов на — некоторое подмножество алгебры . Множество называется коммутантом множество . Ясно, что коммутант является унитальной подалгеброй алгебры . Бикоммутант множество содержить само множество .

Определение 1. Если для *-подалгеброй выполняется равенство тогда называется алгеброй фон Неймана.

Множество называется центром алгеброй .

Пусть — гильбертово пространство над полем комплексных чисел и — алгебра всех ограниченных линейных операторов на . Обазначим через — тождественной оператор на и пусть — решетка проекторов в . Рассмотрим алгебру фон Неймана на т. е. слабо замкнуто *-подалгебру в содержащий оператор и обозначим через операторную норму на Множество — полная ортомодулярная решетка относительно естественного частичного порядка на порожденное конусом — положительных операторов

Два проекторы называется эквивалентными(обозначается через ), если существует частичная изометрия c начальным проектором и конечным проектором т. е. Отношение является также отношением эквивалентности на

Алгебра фон Неймана называется

– конечной, если — конечный проектор;

– полуконечной, если каждый ненулевой проектор из содержит ненулевой конечной проектор;

– бесконечной, если — неконечно;

– собственно бесконечной, если каждый ненулевой проектор из является бесконечным(т. е. неконечным);

– чисто бесконечным или типа III, если каждый ненулевой проектор из является бесконечным.

Говорят, что проектор мажорируется проектором , если существует проектор такой, что , и обозначается . Предположим, что — система ортогональных проекторов в центре , удовлетворяющие условия . Система называется максимальной системой ортогональных проекторов, если для любой системой ортогональных проекторов в центре , с условием , при каждой найдётся такой, что .

Алгебра фон Неймана называется типа I, если она содержит точный Абелева проектор (т. е. — абелева(коммутативная) алгебра фон Неймана).

Это означает, что центральный носитель проектора (т. е. наименьше центральный проектор в мажорирующий ) является тождественным оператором . Алгебра фон Неймана с ненулевым абелевым проектором называется непрерывным. Для произвольная алгебра фон Неймана и может быть разложена единственным способом в прямую сумму алгебр фон Неймана типа (конечный тип), типа (собственно бесконечная типа I), типа (конечно непрерывная), типа (полуконечная, собственно бесконечная, непрерывная) и

Пусть и некоторые алгебры операторов, и — отображение алгебры в алгебру .

Следующая теорема известна с работы [1], и в этом предполагается, что алгебра имеет максимальной системой ортогональных проекторов

Теорема 1. Пусть и алгебры фон Неймана действующие в комплексных гильбертовых пространствах, соответственно и Если ограниченное сюръективное линейное отображение, тогда следующие условия эквивалентны:

(1) — сохраняет нулевое произведение

(2) Существуют такой обратимый элемент и гомоморфизм, для любого имеет место .

Пусть и алгебры матриц -го порядка над алгебры и рассматриваемые в приведенной теореме.

С помощью ограниченное сюръективное линейное отображение сохраняющие нулевое произведение , приведем отображение следующем образом:

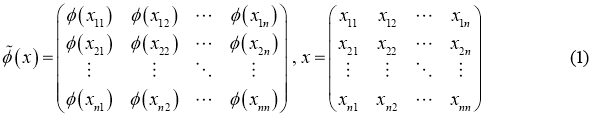
Тогда по теореме 1, мы будем имеет следующей теореме.

Теорема 2. Существуют такой элемент и отображение , для любого элемента имеет место .

Литература:

1. Cui Jianlian and Hou Jinchuan, Linear maps on von Neumann algebras preserving zero products or tr-rank, Bull. Austral. Math. Soc. Vol. 65 (2002).
2. P. Semrl, Local automorphisms and derivations on, Proc. Amer. Math. Soc. 125, 2677–2680 (1997).
3. S. O. Kim, J. S. Kim, Local automorphisms and derivations on Mn, Proc. Amer. Math. Soc. 132, no. 5, 1389–1392 (2004).
4. Sh. Ayupov, K. Kudaybergenov, 2-local derivations and automorphisms on B(H), J. Math. Anal. Appl. 395, no. 1, 15–18 (2012).
5. D. R. Larson and A. R. Sourour, Local derivations and local automorphisms of B(X), Proc. Sympos. Pure Math. 51, Part 2, Providence, Rhode Island 1990, pp. 187–194.