Считается, что Петр I стремился поставить русскую жизнь на западноевропейские основы без учета русских традиций и русского потенциала. В. Ключевский полагал, что царь пытается вооружить российское государство и людей западноевропейскими средствами, умственными и материальными, тем самым ставя государство в один ряд с положением, которое оно завоевало в Европе.
Первоначально Петр I пытался использовать научный и образовательный потенциал развитых европейских стран. Отправка русских людей за границу означала резкую революцию в умах современников, поскольку контакты с иностранцами до Петра не приветствовались, только лицам, выполнявшим дипломатические функции, и торговцам было разрешено уезжать. Однако теперь посланники за границей поощрялись и совершались с применением силы.
В 1699 году король разрешил подданным путешествовать в европейские страны для обучения. Книги были необходимы для распространения знаний, поэтому Петр Великий начал печатать их первыми, в том числе и за рубежом. В 1700 году он передал амстердамскому купцу Яну Тессингу письмо для публикации и продажи в России светских книг, географических карт и т. Д. Но голландец понес убытки: в России было мало потребителей, качество книг было низким. В конце 1600-х годов у Петра I была определенная программа распространения Просвещения в России, которую он объявил в интервью с Патриархом Адрианом в октябре 1699 года. Король жаловался на невежество священников, которые мало знали о грамотности во время церковного обучения, после его смысл, был необходим в жизни. И он высказал мысль о необходимости светского образования. В конце 17 века царь Петр выбрал светскую профессиональную школу в качестве доминирующей образовательной модели.
Петр I Алексеевич (30 мая 1672 г. — 28 января 1725 г.). Математические знания Петра были основательными. Он легко изучал математику. В возрасте 14 лет он услышал от князя Долгорукого, что у последнего был такой инструмент, что вы можете измерять расстояния до его прибытия. Король хотел увидеть инструмент, но он был украден. Петр приказал купить такой инструмент во Франции, куда Долгорукий ездил послом. В 1711 году Петр встретился с немецким математиком Готфридом Вильгельмом Лейбницем в Торгау, присвоив ему и присвоив ему «звание тайного советника с окладом 1000 носителей в год» [1]. Лейбниц направил свои защитные преобразования, которые оказали значительное влияние на реорганизацию России по западноевропейской модели, включая организацию образования.
14 января 1701 года царь издал указ об учреждении в Москве первого в России военно-технического училища при Вооруженных силах. Школа выпустила молодых людей во всех видах услуг, военных и гражданских, которые нуждались в некоторой научной информации или знаниях грамотности; Кроме моряков, навигационное училище покинули моряки, инженеры, артиллеристы, учителя других школ, геодезисты, архитекторы, госслужащие, чиновники, ремесленники и другие.
Математико-навигационное училище предназначалось для воспитания дворянских детей и детей чиновников. Богатые дворяне не хотели, чтобы их дети учились со своими сверстниками. Поэтому во многих отношениях значительная часть обучающихся принадлежала к бедным. Первый набор математических и навигационных школ был определен в 500 учениках от 12 до 17 лет.
Сухаревская башня приобрела огромную известность: в первой четверти XVIII века она считалась центром математики и общего обучения. В Сухаревской башне им удалось сделать астрономические наблюдения и расчеты. Судьба Сухаревской башни была трагичной. В 30-х годах XX века он был снесен.
Во время пребывания Кинга в Англии он встретил Эндрю Фарварсона, профессора Абердинского университета, и пригласил его в Россию. В соответствии с указом Петра Великого об образовании математической и навигационной школы математическая школа была предписана Андрею Даниловичу Фарварсону, навигационной школе Степана Гвина и Ричарда Грейса.
Во время редактирования Фарварсон был сделан перевод и публикация нескольких начал Евклида. В документе 1737 года отмечается важность деятельности А. Д. Фарварсона: с его помощью в России была введена первая математическая подготовка, и почти все они обучались морским наукам на флоте. Только впервые Россия использовала иностранцев в качестве учителей. Сохранилась информация о деятельности первого русского учителя математики — Леонтия Филипповича Магнитского.
Л. Ф. Магнитскому принадлежит несколько учебных пособий по математике, наиболее важным из которых является «Арифметика, или наука о цифрах».... Эта книга — первая базовая работа русского математического образования. Многие поколения россиян учились в этой книге. Все, что было нужно, это помнить правила и применять их к задачам. В то же время «арифметика» Магнитцобыля не обошлась без методологических преимуществ: примеры возрастающих трудностей, интересный круг задач.
В конце курса Фарварсон и Магнитский подали списки выпускников и готовы практиковать сначала в доспехах, затем в военно-морском порядке. Таким образом, 6 студентов закончили обучение почти за 2 года. По некоторым данным, учеников отправляли в качестве учителей в спортивные школы моряков до окончания курса. Затем, в апреле 1703 года, из школы было приказано отправить 2 лучших учеников в Воронеж.
В 1706 году 30 учеников были отправлены из школы в Голландию и Англию для обучения навигации. В 1711 году в школе было 311 штурманов (молодые люди, которые прошли начальный курс навигации). В 1712 году из 517 учеников школы «50 человек были готовы к науке за рубежом, 170 человек к технике» [1]. В 1715 году навигационные классы были перенесены в Санкт-Петербург, и на их основе была создана Морская академия, которой было приказано готовить военно-морских специалистов: Россия стала главной морской державой. Военная наука теперь изучалась во вновь открывшейся академии, а в Московском училище стали преподавать только арифметику, геометрию и тригонометрию. Из профессионала она стала математиком, выполняя функции подготовительной школы для Морской академии.
Школа сыграла большую роль в истории российского образования. Она подготовила ускоренный выпуск значительного числа математиков и штурманов, профессиональных специалистов с широким профилем. Школа математики и мореплавания была первым центром распространения светской науки, прежде всего математики, и первым образовательным учреждением, где готовили учителей математики.
В 1752 году Санкт-Петербургская морская академия была преобразована в военно-морской кадетский корпус, что сделало ее институтом недвижимости вместе с сухопутным кадетским корпусом. Навигационная школа была расформирована, и только дети дворян были переведены из нее в военно-морской кадетский корпус.
В 1714 году специальным указом в провинциальных городах были созданы цифровые школы при епископских домах и крупных монастырях. С этого года математическое образование получило обязательный статус. Состав студентов определялся указом и считался довольно разнообразным. Созданным школам было приказано выделить помещения в епископских домах и монастырях. В 1716 году он был обнаружен в различных
В российских городах 12 цифровых школ. К ним в 1720–1722 годах присоединился еще к 30. В 1727 году в эти школы было набрано около 2000 человек.
Таблица 1
Распределение учеников по сословному составу
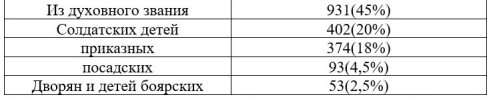
В 1720 году король получил жалобу от горожан. Их дети отправляются в города и содержатся в тюрьмах за охраной. Дети ничему не учатся и просто теряют время. Синод потребовал вернуть детей священства в епархиальные школы, после чего учеников не осталось в 14 из 42 цифровых школ. Учителя вернулись в школу математики и мореплавания. В уцелевших школах почти исключительно учились дети чиновников. Из 2000 студентов осталось только 500.
Таблица 2
Динамика изменения количества учеников
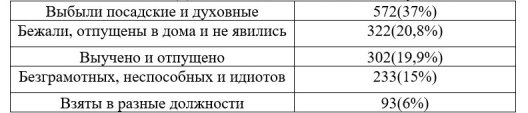
Таким образом, только 395 человек, или около 20 % учащихся, окончили цифровые школы. Из них только 93 человека нашли прямое применение полученным знаниям — их приняли на различные должности.
Классификации во многих школах не было. Это считалось идеальным, когда каждый студент запоминал свою часть предмета на слух, в то время как не было согласованного хора. В 1727 году в Переяславле-Рязанском из 32 учащихся 11 прошли нумерацию, 5 — деление, 5 — сложение, 1 — умножение, 3 — тройные правила, 2 — десятичные дроби, 1 — геометрию, 1 — плоскую тригонометрию. Там не было никаких доказательств или четких объяснений. Студент должен был знать ряд правил и решать проблемы, входящие в их компетенцию.
Профессиональная направленность школ уделяла особое внимание изучению математики в них, тем более что все прикладные науки считались разделами прикладной математики. Благодаря цифровым школам, математика стала основным предметом всех типов школ в первой четверти 18-го века. Цифровые школы просуществовали до 1744 года. На данный момент осталось только 8 из 42 школ. Три крупнейших из них были связаны с гарнизонными школами, остальные прекратили свое существование.
Первые гарнизонные школы были основаны Петром I в 1716 году. Они были размещены в воинских частях и составляли самую низкую категорию военных учебных заведений в России для солдат. Они закрыты или открыты. Они снова были открыты в 1732 году. В 1744 году к гарнизону были присоединены цифровые школы. Таким образом, традиции школы математического плавания были сохранены для гарнизонных школ. Мальчики семи лет были приняты в гарнизонные школы. Они преподавали литературоведение, арифметику, артиллерию и технику, искусство и навыки, необходимые армии. Когда студенту исполнилось 15 лет, он был зачислен в армию.
Феофан Прокопович — один из выдающихся деятелей русского образования в начале 18 века и его наиболее образованные люди. В 1721 году Феофан открыл за свой счет школу для детей-сирот и бедных детей в Санкт-Петербурге, которая стала одной из лучших школ того времени. Изучаемый язык, риторика, история, Римский антиквариат, арифметика, геометрия, графика и музыка. Феофаны оставили большое литературное наследие, где значительная часть была опубликована. Лекции по арифметике и геометрии составляют неопубликованную диссертацию «Первые два и наиболее всеобъемлющие основы математики арифметики и геометрии»... [1]. Курс лекций по математике характеризовался более высоким теоретическим характером.
22 февраля 1702 года Магнитскому был заказан учебник по математике. В результате за 9 месяцев он создал уникальную учебную математическую книгу. Книга имела длинное название. «Арифметика» Магнитского оказала большое влияние на всю последующую русскую математическую литературу.
Книга содержала общие философские рассуждения, советы читателей, общие выводы, которые усиливали образовательный эффект. Учебник содержал информацию по метеорологии, астрономии и навигации, многие знания естествознания и техники. Магнитский определяет арифметику как искусство решения задач со счетом, вычислением. Когда он характеризует числовую систему, Магнитский использует своего рода терминологию, которая оставалась в учебниках математики до конца 18-го века. Все числа первых десяти он назвал пальцами; десятки, сотни — стыками, все остальные числа — композициями. Впервые в русской математической литературе 0 был повышен до числа и ранжирован по пальцам. Книга состоит из двух арифметических книг: Арифметическая политика и Арифметическая логистика.
Арифметическая политика состоит из 5 частей. В первой части оцениваются целые числа и 5 действий — вычитание, сложение, умножение, деление, нумерация. Второй раздел содержит дроби. Дано определение дробей: «Пунктирная линия — ничто иное»... [1]. Третий раздел содержит тройные правила. Везде и во фракциях обратное тройное правило, «правило тройного контракта», отделяется, где возможно предварительное сокращение пропорциональных членов. Четвертый раздел устанавливает правила для ложных правил. Магнитский рассмотрел три случая правила двух ложных определений (когда обе позиции больше желаемых, когда обе меньше, когда одна больше, а другая меньше). В пятом разделе Магнитский разместил учение о прогрессе и восстановлении квадратных и кубических корней.
Арифметическая логистика состоит из двух частей. Первая часть дает письменные и устные обозначения последовательных степеней. После этого Магнитский переходит к другому способу обозначения. Показатель Магнитского представляет собой повторение величины силы, соответствующей числу раз. Второй раздел состоит из двух основных разделов.
Первый раздел посвящен правилам расчета различных форм: (площади треугольника, параллелограмма, трапециевидного и произвольного квадрата, а также правило Герона; площадь круга, сегмента и сектора; поверхность и объем шара, объем шара) призма, пирамида, цилиндр и конус, а также цилиндрические и конические поверхности). Вторая часть второй части представляет решение уравнений. Рассмотрены методы решения квадратных уравнений.
«Арифметика» Магнитского включает в себя: (арифметика натуральных и положительных рациональных чисел, алгебраических символов, квадратных и кубических корней, квадратных и линейных уравнений, простых и несистематизированных элементов тригонометрии). Благодаря учебнику появились квадратные уравнения, десятичные дроби, достижения в русской научной литературе, а в математическом языке появились термины «множитель», «доходность», «пропорция» и «прогрессия».
В 1705 году было опубликовано наглядное пособие по арифметике «Новый метод арифметики теории».... [1] Он содержал первую арифметическую информацию. Другим руководством по арифметике были таблицы умножения, опубликованные в Москве в 1714 году.
В 1703 году в России были опубликованы первые таблицы логарифмов, синусов, касательных и секущих. Эти таблицы содержат семизначные десятичные логарифмы с числами до 10 000, а также логарифмы и натуральные значения для тригонометрии функции. В 1708 году в Москве дважды издавался учебник по геометрии, где царь принимал активное участие в издании и тщательно редактировал весь текст книги.
Большое значение в развитии отечественного образования имеет Московский университет, особенно школа Эйлера. Школа Эйлера столкнулась с рядом проблем. Необходимо было приблизить математику к изучению жизни; необходимо было упростить презентацию; необходимо было освободиться от иностранной терминологии и сделать математику доступной для людей.
В мае 1727 года Леонард Эйлер прибыл в Петербург. В 1728 году началась публикация научного журнала «Комментарии Петербургской академии наук». Второй том содержал три статьи Эйлера, и в последующие годы почти каждое издание ежегодника включало несколько его новых работ. Всего было опубликовано более 400 статей Эйлера. У молодого профессора было много работы: картография, различные обзоры, консультации для корабелов и стрелков, а также подготовка учебных пособий. За время пребывания в России он написал более 90 крупных научных работ. Он выступал с докладами на научных семинарах, читал лекции, участвовал в выполнении технических заказов из государственных ведомств.
В 1735 году перед Академией была поставлена задача выполнить срочный математический расчет, и группа ученых запросила его в течение трех месяцев, а Эйлер выполнил его за три дня. Одной из главных задач, поставленных Эйлеру по прибытии в Россию, была подготовка научных кадров.
Профессиональная направленность школ в начале XVIII в. уделил особое внимание изучению математики. Кроме того, все прикладные науки считались разделами математики, для освоения которых необходимо было изучать теорию. Поэтому первым видом массовых русских школ стали цифровые школы. Несмотря на их низкую эффективность, роль цифровых школ в обеспечении математического образования в России неоспорима. Кроме того, из-за противостояния между цифровыми и епархиальными школами математическое образование проникло в прошлое: Синод решил ввести преподавание на арифметических семинарах и в разделе геометрии. Таким образом, благодаря цифровым школам, математика стала основным предметом во всех типах школ в первой четверти 18-го века.
Литература:
- Полякова Т. С. История Математического образования в России. М.: Изд-во Московского ун-та, 2002.
- Возникновение методико-математических идей в России в XVIII веке. — Текст: электронный//biografia.ru: [сайт]. — URL: http://www.biografia.ru/arhiv/metmat01.html (дата обращения: 10. 02. 2020)
- Эйлер, Леонард. — Текст: электронный // ru.wikipedia.org: [сайт]. — URL: https://ru.wikipedia.org/wiki/ %D0 %AD %D0 %B9 %D0 %BB %D0 %B5 %D1 %80,_ %D0 %9B %D0 %B5 %D0 %BE %D0 %BD %D0 %B0 %D1 %80 %D0 %B4# %D0 %A3 %D1 %87 %D0 %B5 %D0 %BD %D0 %B8 %D0 %BA %D0 %B8







