Мақалада әлемдік ғылымның дамуына өзінің іргелі еңбектерімен үлесін қосқан, Қазақстан тумасы, әл-Фарабидің математикалық мұраларын оқыту туралы айтылған. Әл-Фарабидің әлем ғылымының дамуына қосқан үлесі туралы айтылады. А.Көбесовтың еңбектеріне сүйене отырып әл-Фарабидің геометриялық салуларды, алгоритмдік тәсілдермен шешуі және оның қолданбалы бағыты, оның математикалық мұраларын қазіргі математика курсында ғана емес, жалпы білім беру жүйесіне еңгізу мүмкіншіліктері қарастырылады. Сонымен қатар мақалада әл-Фарабидің басылымға шыққан кейбір еңбектері көрсетілген, әл-Фарабидің математикалық трактатынан алынған кейбір есептер қарастырылған, есептерді шығарудың сызбалары мен түсініктемелері көрсетілген.
Кілттік сөздер:Әл-Фараби, математикалық мұра, математикалық трактатар, салу есептер, алгоритм, алгоритмдік тәсіл, геометриялық салулар.
В данной статье рассматривается математическое наследие Аль-Фараби, который оставил богатейшее научное наследие, оказавший огромное влияние на развития науки. С помощью работ А.Кубесова выявлена возможность внедрения геометрических построений Аль-Фараби в современное образование, благодаря его использованию алгоритмического подхода при решении задач, и его прикладной направленности. А также освещаются некоторые исследования аль-Фараби, которые были опубликованы, рассматриваются некоторые задачи из математических трактатов, геометрические построения, и их решения.
Ключевые слова:Аль-Фараби, матемтическая наследия, математические трактаты, задачи на построения, алгоритм, алгоритмический подход, геометрические построения.
Әл-Фараби (870–950) — ежелгі орта ғасырдың ойшыл, энциклопедист, ұлы ғұламалардың бірі. Қазақстан жерінде, қазіргі қазақ халқын құрған түрік тайпаларының тумасы. Ғылымның барлық саласындағы біліктілгінің арқасында, Аристотельден кейіңгі екінші ұстаз — «ал-муаллимас-сани» атағын берген Ортағасыр Шығыс ғалымдарының арасында алар орны ерекше [1].
Әл-Фараби — Ибн Сина, әл-Бируни, Омар Хайям, Наср ад-Дин ат-Туси және т. б. ғалымдар мен философтар шыққан орта Азия және Қазақстан, жалпы шығыс мұсылман елдерінде үдемелі әлеуметтік-философиялық ойлардың ірге-тасын қалаушылардың бірі болып саналады. Философиялық және логикалық шығармаларлан басқа әл-Фараби көптеген жаратылыстану-математикалық және натурфилософиялық еңбектері бар. Ол артынан Шығыс пен Батыс ғылымының дамуына орасан зор үлес әкелген бай ғылыми мұралар қалдырды. Бұл ойшылдың мұраларын зерттеу, оның әлем ғылымына және өркениетке тигізген әсерін айқындау әлі күнге дейін өзектілігін жойған жоқ.
Әл-Фарабидің ғылыми еңбектерінде физика-математика саласындағы зерттеулер айрықша орын алады. Шығыс ислам педагогикасы және математика тарихы саласындағы ірі ғалымдардың бірі, Ауданбек Көбесовтің (1932–2008) әл-Фарабидің математикалық мұраларын зерттеудегі үлесі мол. Оның «әл-Фарабидің математикалық мұралары», «Математикалық трактаттар» атты еңбектері, әл-Фарабидің мұраларын зерттеуші шетелдік ғалымдар жоғары бағалап, Мичиган университетінде (2007, 2010), ал «Птоломейдің «Алмагест» кітабына түсініктемелері» Калифорния университетінде (2008) цифрландырылады [3] [4].
Әл-Фарабидің физика-математикалық шығармаларының, аудармаларының және жазбаларының негізгі мәліметтері Ауданбек Көбесовтың еңбектерінде келтіріледі. Ауданбек Көбесов өзіне дейін ашылмаған әл-Фараби-дің, «Табиғат сырын геометриялық фигуралар арқылы танытарлық рухани айла-әрекеттер» — атты геометриялық трактатын ашты. Бұл трактатта әл-Фараби қолданбалы геометрияға, геодезияға, архитектура және техникаға арнаған. Ол кіріспемен 10 кітаптан (мақалат) тұрады. Әл-Фараби бұл трактатында Шығыс орта ғасыр математикасының жалпы сипаттамасына сай келетін геометриялық құрылымдардың алгоритмдеріне басты назарын аударған [2].
Трактаттың бірінші кітабында сызғыш пен циркуль арқылы сызылатын қарапайым сызбалар қарастырылған. Екінші кітабында берілген кесіндіге сызылған көпбұрыштарға арналған, ал үшінші кітабы шеңберге іштей сызылған көпбұрыштарға арналған. Төртінші кітабында үшбұрыш пен дұрыс көпбұрыштың маңында сипатталған шеңберді сызуға арналған есептер шешілсе, бесінші кітабында үшбұрышқа іштей сызылған шеңберге қатысты есептер қарастырылады. Алтыншы кітабы дұрыс көпбұрышқа ішетей сызылған дұрыс көпбұрыштар қарастырылады. Кейбір есептерінде үшбұрыштарды сызу гомотетия әдістеріне негізделген. Жетінші кітабында үшбұрышты тең бөлікке бөлу, оны бірнеше есе үлкейту және кішірейту, мұнда да гомотетия әдісі қолданылады. Сегізінші кітабында әр түрлі шарттарды қанағаттандыратын паралллелограм мен трапецияны түзулермен бөлу қарастырылған. Бұнда да гомотетия әдісі қолданылған. Тоғызыншы кітабында шаршының n2 шаршылардан түрлендірулері, шаршыны 2n2 және n2+m2 шаршылардан құру және кері есептері, үш тең шаршыдан шаршыны құрудың әр түрлі жолдары қарастырылған. Осы кітабында әл-Фараби қолөнершілердің шаршыны үш есе көбейту жолдарына пікір жазған. Оныншы кітабы сферада сызылған әр түрлі сызбаларға арналған, оның ішінде сфераны дұрыс сфералық көпбұрыштарға бөлу, төбелері көпбұрыштың төбелері болатын іштей сызылған балама көпжақтыларға арналған.
Әл-Фарабидің геометриялық трактаты құрылымдық геометрияның дамуына үлкен рөл атқарды. Бұл еңбекте айтылған көп идеялар алдағы уақытта Шығыс Орта ғасыр және Европаның жаңару дәуіріндегі математиктерімен жетілдірілді.
Геометрияның салау есептеріне келер болсақ, ол қазіргі күнде геометрияны оқытудың ерекше орын алатын, мектеп геометрия курсында мазмұнды орыны бар, бөлінбес бір бөлігі болып табылады. Әл-Фарабидің трактатында көптеген геометриялық салу есептері және дәл сызуға мүмкін болмайтын сызбаларды, сызғыш пен циркуль арқылы сызуға арналған ерекше алгоритмдер ұсынылады. Әл-Фараби өзінің есепке деген ерекше көзқарасына сай, бұндай салу есептерін мейлінше дәл сызуға арналған алгоритмдер келтірген. Бұрыш трисекциясы, шеңберге іштей сызылған дұрыс көпбұрыштар және т. б. циркуль мен сызғыш арқылы дәл сызылмайтын классикалық ежелгі есептер ерекше назар аудартады. Ғалымдар, инженерлер мен архитекторлар және т. б. әрдайым дұрыс көпбұрышқа ерекше мән берген.
Мысал ретінде әл-Фарабидің математикалық трактатында келетін кейібір есептерді, «информатика» және «математика» пәндерінде АКТ құзырлылықты пайдалана отырып оқытуға болады. Бұған әл-Фарабидің зерттеулерінің бірегейлігі яғни математикалық проблемаларды алгоритмдік тәсілдермен шешуі және жасалған зерттеулерінің қолданбалы бағыты мүкіндік туғызады.
АКТ-ны қолдануда және информатика мен информатизация негізінде алгоритм ұғымы жатқандықтан, әл-Фарабидің жүргізген зерттеулерінің алгоритмдік тәсілдері және қолданбалы бағыты электрондық оқытуда дидактикалық құралдарды жасауға мүмкіндік береді. Егер қолданбалы бағытынан қарайтын болсақ, математиканы табиғи құбылыстар мен процесстер бағытында үйреніп зерттеу, және оны практика жүзінде қолдану әл-Фарабидің басты қағидаларының бірі болып табылады. Осыған байланысты «рухани айла-әрекеттер» математиканың бір бөлігі ретінде қарастыру (қазіргі қолданбалы математиканың протатипі ретінде) өте құнды.
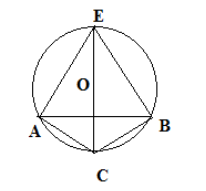
1 сурет
Шеңбердің доғасы беріледі (доға сызылулы). Берілген доға бойынша шеңбердің центрімен радиусын тауып, доғаны шеңберге толықтыру керек (1 сурет) [2]. Доғаның екі шетінен сәйкесінше А және В нүктелерін белгілеп аламыз. А және В нүктесін қосып хорда сызамыз. Сызылған хорданың ортасына перпендикуляр жүргіземіз. Хордаға сызылған перпендикулярмен доғаның қиылысқан нүктесін С нүктесі деп алып, оны А және В нүктесімен қосамыз (Теорема: Хорданың орта перпендикуляры шеңбердің центрінен өтеді.). Хордаға сызылған перпендикулярмен доғаның қиылысқан нүктесін С нүктесі деп алып, оны А және В нүктесімен қосамыз. АС және ВС кесіндісіне сәйкесінше перпендикуляр болатын түзулер сызамыз, және хорданың центріне сызылған перпендикулярмен қиылысқан нүктесін Е деп алайық. Е және С кесіндісінің ортасы О нүктесі доғаның радиусы болады. О нүктесі СВЕ үш бұрышына сырттай сызылған шеңбердің центрі болады. Ол шеңбер АВ доғасын толықтыратын шеңбер болады. Бұл сызбаны әл-Фараби басқа сызбалары сияқты дәлелдеусіз келтірген.
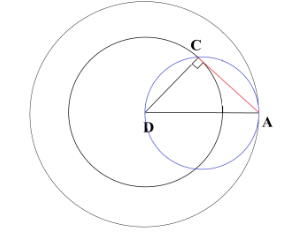
2 сурет
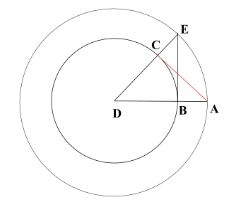
3 сурет
Центрі D болатын шеңбер берілген. Шеңберден тыс жатқан (2 сурет) [2]. А нүктесінен жанама жүргізу керек. A және D арасына түзу жүргізіп, шеңбермен қиылысу В нүктесін белгілейміз. Радиусы DA-ға тең болатын шеңбер сызамыз. В нүктесінен перпендикуляр жүргізіп, оның радиусы DA-ға тең болатын шеңбермен қиылысатын Е нүктесін белгілейміз. ЕD кесіндісін жүргізіп оның шеңбермен қиылысатын С нүктесін белгілейміз. А және С нүктелерін қоссақ, ол берілген шеңбердің жанамасы болып табылады. Себебі, екі үшбұрыш ΔDCA=ΔDBE болғандығынан <АСD тік бұрыш болады. Сондықтан АС шеңберге А нүктесінен жүргізілген жанама болады.
Екінші шешімі, диаметрі DA кесіндісіне тең болатын шеңбер сызсақ, ол берілген шеңберді бір С нүктесінен қияды. D және C нүкетелерін қоссақ ол берілген шеңбердің радиусы болады. СА және СD кесінділері соңғы сызылған шеңбердің диаметріне тірелгендіктен
Осылайша геометриялық сызбаларға келтірілген есептер, оқушылардың геометриялық сызбаларды оқудағы үлкен жетістісктерге жетуге мүмкіндіктері болады. Математиканы оқушыларға, жоғарыда келтірілген сызбалар арқылы, электронды оқыту әдісімен, ал информатиканы геометриялық сызбаларды сызудағы алгоритмдік әлістерімен оқыту арқылы үйренуге болады.
Әл-Фараби-дің геометриялық салу есеперін сызудағы барлық әдіс тәсілдерді көрсететін, мультимедиялық білім алатын русурстарға ерекше қызығушылық артуда. Әл-Фарабидің математикалық мұрасын зерттеу аясында, қазіргі таңда Абай атындағы Қазақ ұлттық педагогикалық университетінде осындай ресурстарды дайындау жұмыстары жүргізілуде.
Әдебиет:
- Кубесов А. К. Математическое наследие аль-Фараби. Алма-Ата, «Наука», 1974. — 246 с.
- Аль-Фараби, Математические трактаты. — Алма-Ата, 1972. 318 с.
- Бидайбеков Е. Ы., Бостанов Б. Г., Камалова Г. Б. The mathematical heritage of Al-Farabi by A.Kubesov in modern conditions of educations // Матер. IX Межд. конгресса ISAAC. 5–9 августа 2013 г. Краков, 2013. C. 33–34.
- Carry J. Tee (University of Aucland), Kubesov A. K. The Mathematical Heritage of al-Farabi // Journal for the history of Arabic science. 1978. № 1. P. 150–153 (in Russian).
- И. И. Ильясов, Ш. Г. Мулдашев. Әл-фарабидің кітабынан алынған кейбір есептерге түсініктеме./«Математикалық білім: жағдайы, мәселелері, болашағы» атты халықаралық ғылыми — практикалық конференция материалдары. — Ақтөбе, 2019. — Б.71–76.

